
- •Глава 1. Интерполирование
- •Постановка задачи интерполирования
- •1.2. Единственность интерполяционного многочлена
- •. Интерполяционный многочлен Лагранжа
- •1.4. Погрешность интерполяционной формулы Лагранжа
- •. Конечные разности и их свойства
- •1.6. Первая интерполяционная формула Ньютона
- •1.7. Вторая интерполяционная формула Ньютона
- •1.8. Интерполяционная формула Гаусса
- •1.10. Численное дифференцирование
- •Глава 2. Численное интегрирование
- •2.1. Общие замечания
- •Глава 3. Численные методы решения алгебраических и трансцендентных уравнений
- •3.1. Вводные замечания
- •3.2. Отделение корней
- •3.3. Метод половинного деления
- •3.5. Метод Ньютона (метод касательных)
- •3.6. Комбинированный метод
- •3.7. Метод итерации (метод последовательных приближений)
- •Глава 4. Решение систем линейных уравнений
- •4.1. Метод Гаусса (схема единственного деления)
- •4.2. Вычисление определителей
- •4.3. Вычисление обратной матрицы
- •4.4. Некоторые сведения из линейной алгебры
- •Рассмотрим систему линейных алгебраических уравнений
- •Вычитая второе равенство из первого, получаем
- •4.6. Приведение линейной системы к виду,
- •4.7. Метод Зейделя Пусть система линейных алгебраических уравнений приведена к виду
- •Глава 5. Обработка результатов наблюдений
- •5.1. Постановка задачи
- •5.2. Приближение функции, заданной таблично,
- •Глава 6. Численные методы решения
- •6.1. Методы решения задачи Коши. Вводные замечания
- •6.2. Решение дифференциальных уравнений
- •6.3. Метод Эйлера Пусть дано дифференциальное уравнение
- •6.4. Уточненный метод Эйлера Рассмотрим дифференциальное уравнение
- •6.6. Методы Рунге – Кутта Пусть дано дифференциальное уравнение
- •6.7. Метод Милна
- •6.8. Приближенное решение систем дифференциальных
- •6.9.Краевые задачи для обыкновенных дифференциальных
- •6.10. Решение краевых задач
- •6.11. Метод прогонки Рассмотрим линейную систему уравнений (6.54). Преобразуя первые (n-1) уравнения:
- •Глава 7. Численное решение дифференциальных уравнений в частных производных
- •7.1. Классификация дифференциальных уравнений
- •7.2. Метод сеток решения краевых задач
- •7.3. Погрешность аппроксимации дифференциальных уравнений
- •7.4. Аппроксимация граничных условий
- •7.6. Метод сеток для уравнений
7.2. Метод сеток решения краевых задач
для дифференциальных уравнений эллиптического типа
Рассмотрим дифференциальное уравнение эллиптического типа
![]() (7.2)
(7.2)
Это уравнение называют уравнением Пуассона (С. Пуассон (1781 – 1840) – французкий механик, физик и математик).
Первая краевая задача, или задача Дирихле для уравнения Пуассона, ставится следующим образом. Найти функцию u=u(x,y), удовлетворяющую внутри некоторой области D уравнению (7.2), а на границе Г – условию
![]() ,
(7.3)
,
(7.3)
где
![]() - заданная непрерывная функция.
- заданная непрерывная функция.
Одним из самых распространенных методов численного решения дифференциальных уравнений в частных производных является метод сеток (метод конечных разностей), который заключается в следующем.
Проводим на плоскости х0у два семейства параллельных прямых
![]() ;
;
![]() .
.
Точки пересечения этих прямых назовем узлами. Узлы имеют координаты:
![]() ,
,
![]() .
.
Условимся на рисунках данной главы указывать только индексы узла. Например, узел (xi, yk) обозначается через (i, k).
Два узла называются соседними, если они удалены друг от друга в направлении оси 0х или 0у на расстояние, равное шагу сетки h или l соответственно. Таким образом, расположение узла (xi, yk) и его соседних узлов выглядит следующим образом (7.1).

 (i,
k+1)
(i,
k+1)
l
h

![]()
Рис. 7.1
Будем рассматривать
только те узлы, которые принадлежат
области
![]() .
Разобъем узлы области
.
Разобъем узлы области
![]() на внутренние и граничные. Некоторый
узел (xi,
yk)
будем считать внутренним, если он сам
или четыре соседних узла принадлежат
области
.
Узлы области
,
у которых хотя бы один соседний узел не
принадлежит области
,
называется граничным. Множество
внутренних узлов обозначим через
на внутренние и граничные. Некоторый
узел (xi,
yk)
будем считать внутренним, если он сам
или четыре соседних узла принадлежат
области
.
Узлы области
,
у которых хотя бы один соседний узел не
принадлежит области
,
называется граничным. Множество
внутренних узлов обозначим через
![]() ,
множество граничных узлов – через Г*.
,
множество граничных узлов – через Г*.
На рис. 7.2 внутренние узлы помечены знаком «о», граничные – знаком «*»
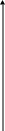
 у
у






0 х
Рис. 7.2
Рассмотрим дифференциальное уравнение (7.2) во всех внутренних узлах:
![]() .
(7.4)
.
(7.4)
Заменим частные производные второго порядка разностными отношениями:
![]() (7.5)
(7.5)
![]()
где через Uik обозначено приближенное сеточное значение решения уравнения (7.2) в узле (xi, yk).
Подставляя (7.5) в (7.4), получим для каждого внутреннего узла приближенное равенство
![]()
![]() .
(7.6)
.
(7.6)
Рассмотрим граничные узлы, т.е. узлы (xi, yk) Г*. Известно, что по условию (7.3). Поэтому, если узел попадает на границу Г области D, значение Uik можем вычислить, используя это условие. Однако, как правило, граничные узлы не будут попадать на границу Г. Пусть узел (xi, yk) не попадает на границу Г. В этом случае значение Uik положим равным значению функции в точке границы Г, ближайшей к этому узлу.
Иногда значение Uik полагают равным значению функции в точке Г, ближайшей к рассматриваемому гра ничному узлу в направлении оси 0х (рис. 7.3):
Uik=U(B)
![]() (xi,
yk)
Г*.
(7.7)
(xi,
yk)
Г*.
(7.7)
Объединяя равенства (7.6) и (7.7), получим неоднородную линейную систему, в которой число уравнений равно числу неизвестных. Доказанно, что эта система имеет решение и притом единственное. Решив ее, получим приближенные значения искомого решения в узлах сетки.
Рассмотрим частный случай уравнения (7.2), который получается при f(x,y)=0
![]() .
(7.8)
.
(7.8)
Это уравнение называют уравнением Лапласа (П. Лаплас (1749 – 1827) – французский математик, физик и астроном).
Конечно – разностные уравнения (7.6) для уравнения Лапласа запишутся в виде
![]() .
(7.9)
.
(7.9)
Наиболее простой вид эти уравнения имеют при h=l:
![]()
или![]() .
(7.10)
.
(7.10)



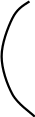 у
у


 М
В
М
В
![]()
0 ч
Рис. 7.3
Объединяя (7.7) и (7.10), получим линейную систему уравнений. Решив систему, получаем приближенные значения решения уравнения (7.8), удовлетворяющего условию (7.3), в узлах сеточной области.
