1.7. Вторая интерполяционная формула Ньютона

Пусть функция задана таблицей своих значений в равноотстоящих точках и пусть точка интерполирования х лежит вблизи конечной точки х_n таблицы или справа от нее. Для уменьшения погрешности интерполирования узлы интерполяции следует использовать в порядке х_n, x_n-1, x_n-2,…, x₀. Ищем интерполяционный многочлен в виде

(1.20)

Неизвестные коэффициенты а₀, а₁, …, а_n находим из условий (1.1) аналогично тому, как находили коэффициенты первой интерполяционной формулы Ньютона. положим в (1.20)

Тогда , т.е. .

Полагаем в (1.20) :

; .

Далее полагаем в (1.20) :

;

;

.

Продолжая аналогичные вычисления, получаем

.

(Доказать эту формулу можно при помощи метода математической индукции).

Подставляя полученные значения коэффициентов в (1.20), имеем

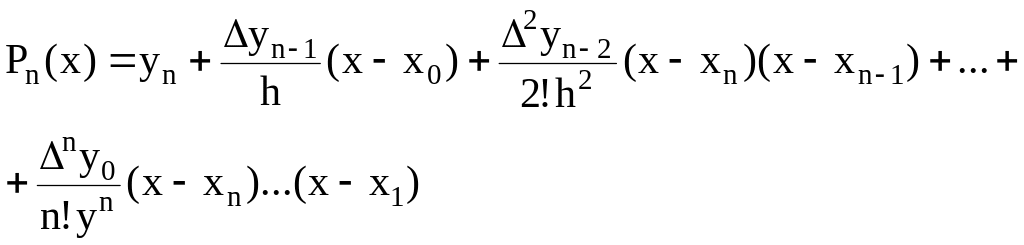(1.21)

Полученная формула носит название второй интерполяционной формулы Ньютона, или интерполяционной формулы Ньютона для интерполирования в конце таблицы.

На практике вторая интерполяционная формула Ньютона, как и первая, применяется в преобразованном виде. Вводим переменную

.

Тогда

;

и т.д.

После введения новой переменной q формула (1.21) примет вид

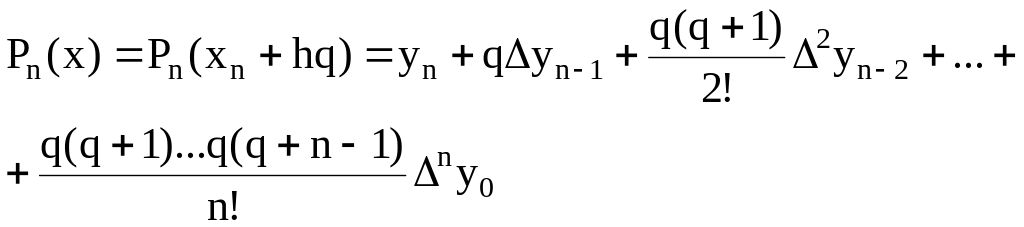(1.22)

Отметим, что вторая интерполяционная формула Ньютона содержит конечные разности, расположенные в нижней косой строке таблицы конечных разностей.

Погрешность второй интерполяционной формулы Ньютона запишется в виде

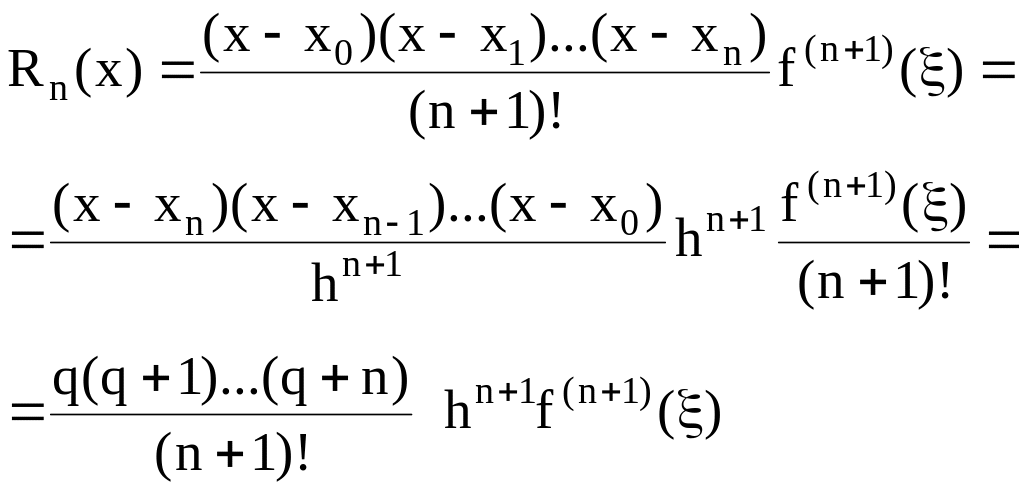, (1.23)

где - некоторая точка интервала, содержащего узлы интерполяции.

Получены первая и вторая интерполяционные формулы Ньютона. При записи этих формул используются все заданные точки таблицы (х₀, х₁, …, х_n).

Естественно, эти формулы дают один и тот же многчлен в разных формах записи. На практике применяются обычно многочлены невысоких степеней. Для построения многочлена степени m ( ) требуется (m+1) точка. Если точка интерполирования х лежит в начале таблицы, строим по первой интерполяционной формуле Ньютона с использованием точек х₀, х₁, …, х_m.

Первая интерполяционная формула Ньютона запишется в этом случае в виде

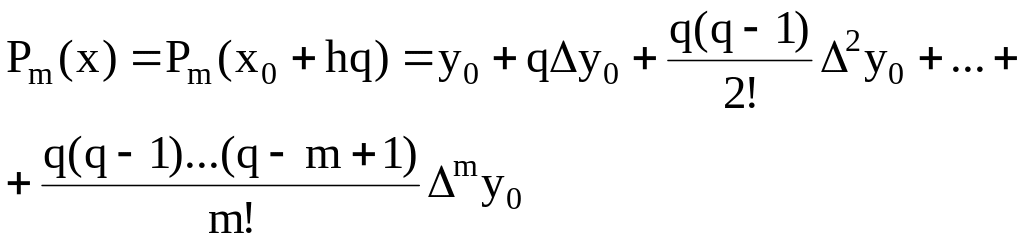, (1.24)

где .

Если же точка интерполирования х лежит в конце таблицы, строим по второй интерполяционной формуле с использованием точек х_n, x_n-1, x_n-2,…, x_n-m. Вторая интерполяционная формула Ньютона запишется в этом случае в виде

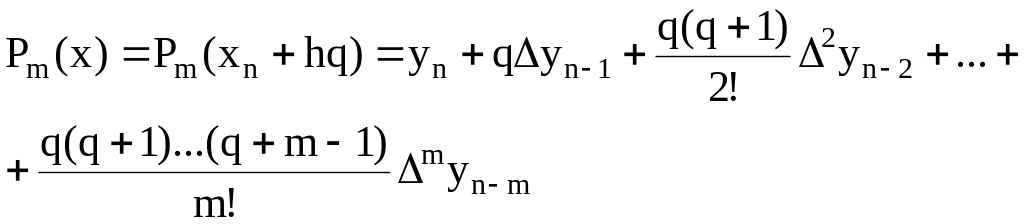, (1.25)

где .

Чтобы выбрать степень интерполяционного многочлена, нужно установить связь между производными и конечными разностями. Пусть функция y=f(x) имеет непрерывные производные до порядка (n+1) на отрезке [a,b], содержащем узлы интерполирования. По определению производной имеем

.

Отсюда вытекает, что при малых h

.

Далее находим

.

Применяем дважды правило Лопиталя:

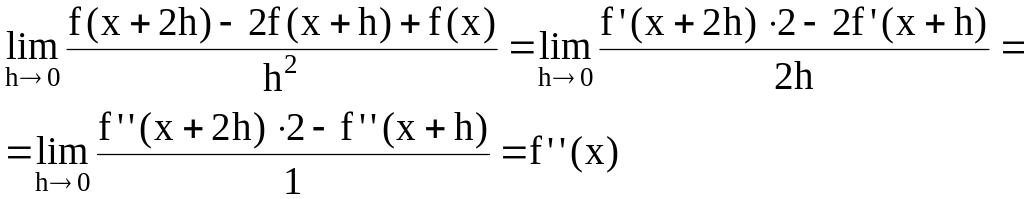
Таким образом,

.

Отсюда при малых h имеем

.

Аналогично можно показать, что

. (1.26)

Из формулы (1.26) получаем, что , т.е. разность пропорциональна . Если h достаточно мало, с ростом m быстро убывает. Значение m, при котором практически постоянны, дает нам целесообразную степень интерполяционного многочлена. Если продолжать построение таблицы конечных разностей, происходит накопление погрешностей, и значения конечных разностей получаются все более неточными.

Несколько слов об оценке погрешности интерполяционных формул Ньютона. Пусть интерполяционный многочлен есть многочлен степени m, записанный по одной из формул (1.24) или (1.25). тогда погрешность первой интерполяционной формулы Ньютона запишется в виде

, (1.27)

где .

Погрешность второй интеполяционной формулы Ньютона запишется в виде

, (1.28)

где .

Формулы (1.27) и (1.28) содержат , где . На практике часто бывает трудно, иногда же просто невозможно оценить величину .

Рассмотрим простой, хотя и очень грубый способ такой оценки. Согласно формуле (1.26) . Предполагаем, что производная на отрезке [a,b] меняется медленно. Тогда приближенно можно взять

.

Если расположение точки на отрезке [a,b] неизвестно, вместо лучше всего взять среднее арифметическое всех вычисленных конечных разностей порядка (m+1). Обозначим эту величину через . Тогда . (1.29)

Подставляя (1.29) в (1.27), получим формулу для оценки погрешности первой интерполяционной формулы Ньютона

(1.30)

Подставляя (1.29) в (1.28), получим формулу для оценки погрешности второй интерполяционной формулы Ньютона

. (1.31)

Пример. Функция f(x) задана таблицей своих значений:

x	1,0	1,1	1,2	1,3	1,4	1,5	1,6
f(x)	0,00000	0,04139	0,07918	0,11394	0,14613	0,17609	0,20412

Требуется вычислить f(1,03) и f(1,56).

Строим табл. 1.3 конечных разностей заданной функции.

Таблица 1.3

1,0	0,00000
		4139
1,1	0,04139		-360
		3779		57
1,2	0,07918		-303		-11
		3476		46		-1
1,3	0,11394		-257		-12
		3219		34		-2
1,4	0,14613		-223		-14
		2996		30
1,5	0,17609		-193
		2803
1,6	0,20412

Разности четвертого порядка можно считать практически постоянными. Поэтому для приближенного вычисления значений функции и заданных точках будем использовать интерполяционный многочлен четвертой степени. Тогда точка х=1,03 лежит в начале таблицы. Используем первую интерполяционную формулу Ньютона (1.24) при

x₀=1,0; h=0,1; m=4; .

Конечные разности, используемые в этой формуле, располдожены в верхней косой строке таблицы:

.

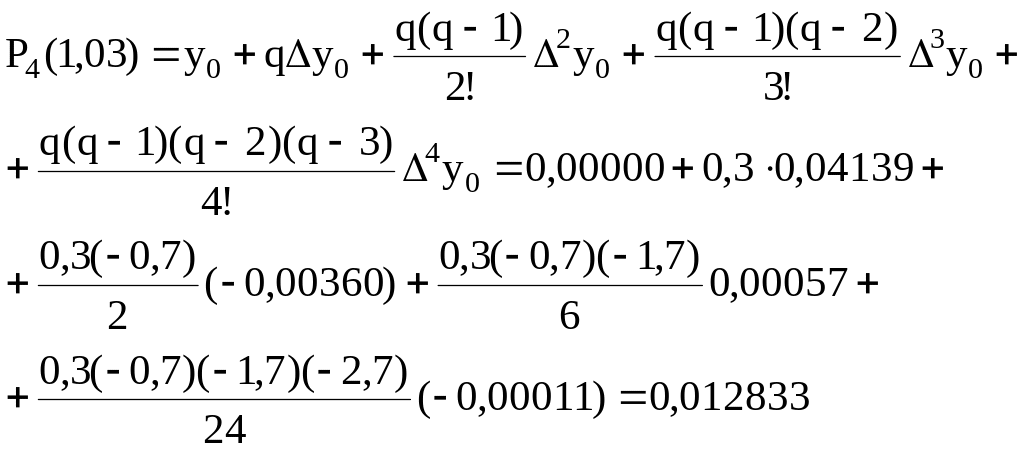Вычисления производим с шестью знаками после запятой. В ответе последний знак отбрасываем:

.

Точка х=1,56 лежит в конце таблицы. Используем вторую интерполяционную формулу Ньютона (1.25) при

x_n=1,6; h=0,1; m=4; .

Конечные разности, используемые в этой формуле, расположены в нижней косой строке таблицы:

.
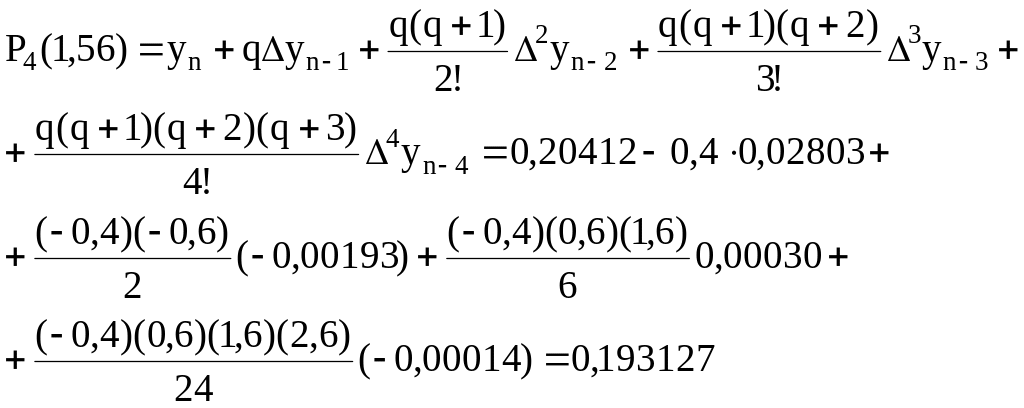