1.8. Интерполяционная формула Гаусса

Пусть функция f(x) задана таблицей своих значений в равноотстоящих узлах и пусть точка интерполирования х находится в середине таблицы между узлами интерполирования и , т.е. <x< . Предположим, что точка х расположена ближе к . При построении интерполяционного многочлена узлы используем в порядке их удаления от точки х, т.е. в порядке

x_k, x_k+1, x_k-1, x_k+2, x_k-2, …, x_k+m, x_k-m ( ).

Ищем интерполяционный многочлен в виде

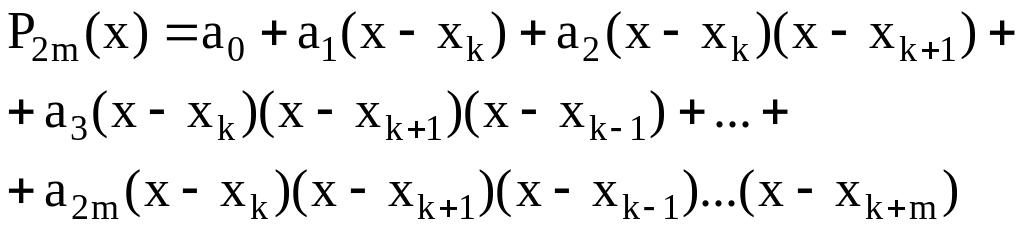. (1.32)

Полагая в (1.32) x= x_k и используя (1.1), имеем

, т.е. .

Далее, полагая в (1.32) x= x_k+1 и используя (1.1), получаем

;

.

Отсюда

.

Для вычисления коэффициента полагаем в (1.32) , а также используем формулу (1.1) и значения найденных коэффициентов и :

;

.

Отсюда

.

Аналогично находим

; ;…; .

Подставляя найденные коэффициенты в (1.32), получаем

. (1.33)

Получена интерполяционная формула Гаусса (К. Гаусс (1777 – 1855) – выдающийся немецкий математик, астроном, физик и геодезист).

Вводим новую переменную

.

Тогда

;

…

.

После введения новой переменной q интерполяционная формула Гаусса запишется в виде

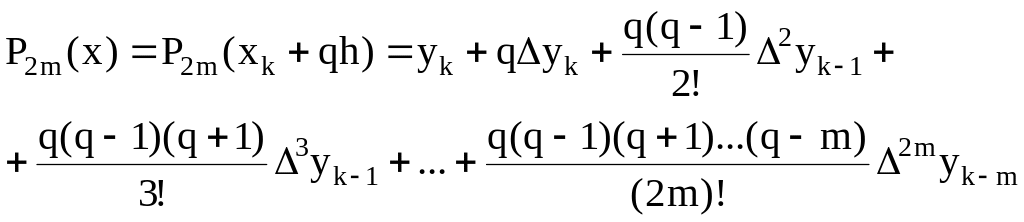(1.34)

где .

В табл. 1.4 показано, как расположены конечные разности, входящие в интерполяционную формулу Гаусса.

Таблица 1.4

Погрешность интерполяционной формулы Гаусса записывается в виде

где ; .

При грубой оценке погрешности на практике согласно формуле (1.26) можно положить

,

где - среденее арифметическое всех вычисленных конечных разностей порядка (2m+1).

Замечание 1. Если при практических расчетах возникает необходимость в построении интерполяционного многочлена нечетной степени, его можно получить из формулы (1.34) путем отбрасывания последнего слагаемого:

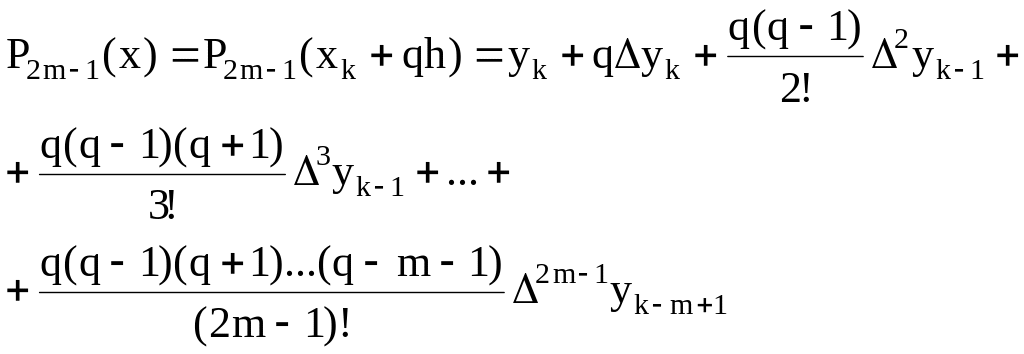(1.36)

При этом погрешность запишется в виде

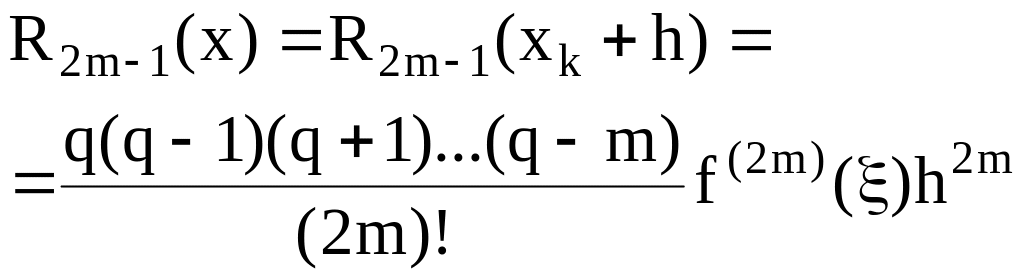(1.37)

Замечание 2. При выводе интерполяционной формулы Гаусса (1.34) предполагалось, что точка интерполирования х лежит ближе к x_k, чем к x_k+1. Если заданная точка х лежит ближе к x_k+1, можно вывести формулу, аналогичную формуле (1.34), используя узлы интерполяции в следующем порядке:

x_k+1, x_k, x_k+2, x_k-1, x_k+3, … .

При отсутствии новой формулы можно воспользоваться формулой (1.34).

Пример. Для функции, заданной таблицей своих значений в примере параграфа 1.7, вычислить приближенно значение в точке х=1,22.

Точка х=1,22 лежит в середине таблицы между узлами x_k=1,2 и x_k+1=1,3.

Воспользуемся интерполяционной формулой Гаусса (1.34) при

m=2; x_k=1,2; h=0,1; .

Значения берем из табл. 1.3:

;

.

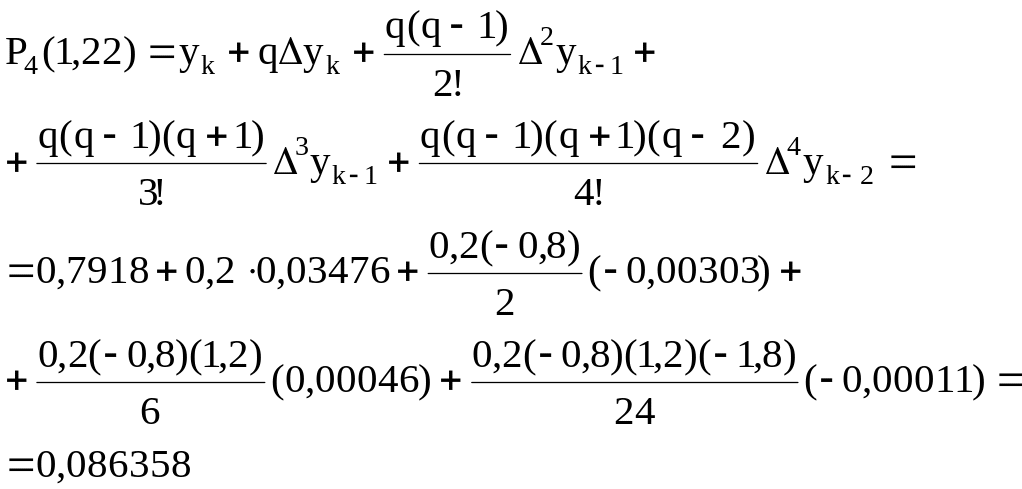1.9. Обратное интерполирование

Пусть функция y=f(x) задана таблицей своих значений . В предыдущих параграфах рассмотрено, как по заданному значению аргумента приближенно найти значение функции. зАдача обратного интерполирования заключается втом, чтобы по заданному значению функции y* найти аргумент x*, при котором . Предположим, что на отрезке [a,b], содержащем узлы интерполяции, функция f(x) монотонна. Тогда существует однозначная обратная функция x=F(y). Она задана той же таблицей значений, что и функция y=f(x), только в роли значений аргумента выступают значения , а - соответствующие им значения функции. Обратное интерполирование в этом случае свелось к обычному интерполировнию для функции x=F(y). Строим интерполяционный многочлен , воспользовавшись, например, интерполяционной формулой Лагранжа. Подставляя в заданное значение y*, получим .

Рассмотрим второй способ нахождения х*, который применим ко всякой функции f(x). Не меняя ролями функцию и аргумент, записываем интерполяционный многочлен по той или иной формуле. Неизвестное значение х* находим приближенно, решая уравнение =у*. Если число узлов велико, то этот способ нахождения х* приводит к решению алгебраического уравнения высокой степени. Различные методы решения таких уравнений будут рассмотрены в гл. 3. Ниже остановимся на методе итерации. Будем рассматривать только случай равноотстоящих значений аргумента, т.е.

.

Пусть для определенности у* находится между у₀ и у₁. Строим интерполяционный многочлен по первой интерполяционной формуле Ньютона. Уравнение =у* принимает вид

. (1.38)

Разрешим это уравнение относительно q, стоящего при разности первого порядка. Получим

(1.39)

Метод итерации (метод последовательных приближений) заключается в следующем. Выбираем начальное приближение .

Подставляя в правую часть равенства (1.39), получаем

Подставляя вычисленное в правую часть равенства (1.39), получаем

Аналогично по находим , а затем и т.д.:

. (1.40)

В значительном числе случаев этот процесс сходится и дает в пределе точное решение уравнения.

На практике интерполяционный процесс заканчивают, когда два соседних приближения совпадают в пределах заданной точности. Последнее вычисленное приближение принимается за решение уравнения (1.38) – q*.

Найдя q*, определяем x* из соотношения

,

т.е. .

Пример. Функция y=f(x) задана таблично:

Х	0,5	0,6	0,7	0,8	0,9
у	1,6487	1,8221	2,0138	2,2255	2,4596

Найти значение аргумента х*, для которого у*=1,7333. Строим табл. 1.5 конечных разностей заданной функции.

Таблица 1.5

0,5	1,6487
		1734
0,6	1,8221		183
		1917		17
0,7	2,0138		200		7
				24
		2117
0,8	2,2255		224
		2341
0,9	2,4596

Так как , для нахождения q* воспользуемся уравнением (1.39). подставляем в (1.39) у*, у₀ и конечные разности из табл. 1.5:

;

.

Подставляем найденное в правую часть уравнения (1.41):

.

Аналогично находим

.

Четыре знака после запятой у и совпали. Отсюда

;

.