7.3. Погрешность аппроксимации дифференциальных уравнений

эллиптпческого типа конечно – разностыми уравнениями

При применении метода сеток для решения краевых задач дифференциальные уравнения заменяются конечно – разностными уравнениями. Выясним, чему равна погрешность такой замены. Рассмотрим, например, погрешность, получаемую в результате замены дифференциального уравнения (7.8) конечно – разностным уравнением (7.10).

Используя формулу Тейлора, значения функции , , , запишем в виде

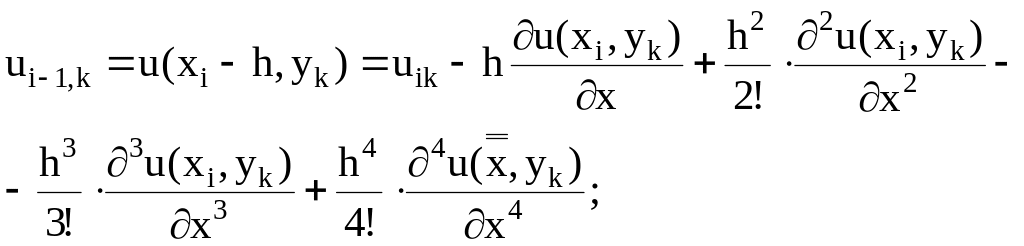
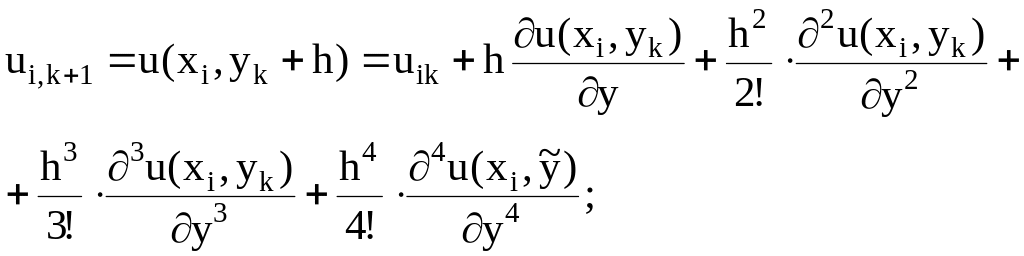(7.11)

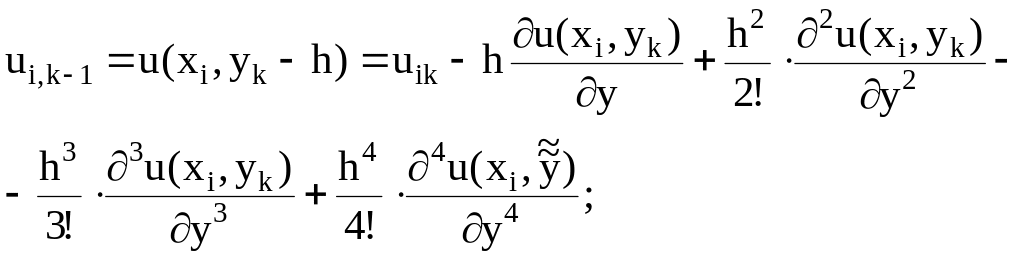
где

, , ,

.

Складывая равенства (7.11), получим

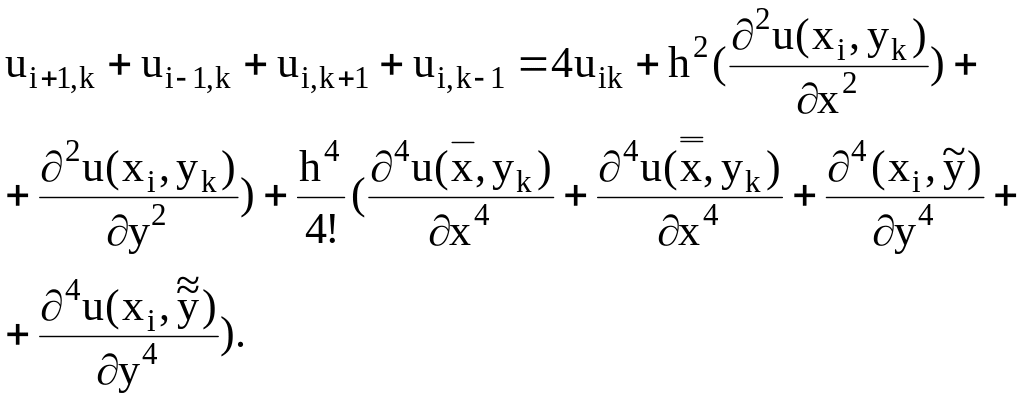
Отсюда

,

где

.

Если ввести обозначение

,

то

.

Таким образом, погрешность замены дифференциального уравнения (7.8) конечно – разностным уравнением (7.10) имеет порядок h². Такой же порядок имеет погрешность замены дифференциального уравнения (7.8) конечно – разностным уравнением (7.9), а также погрешность замены дифференциального уравнения (7.2) конечно – разностным уравнением (7.6).

7.4. Аппроксимация граничных условий

В параграфе 7.2. указывалось, что в граничных узлах значения функции можно заменить значением функции в точке границы Г, ближайшей к рассматриваемому граничному узлу в направлении оси 0х.

Очевидно, что погрешность этой замены имеет порядок h, так как для вычисления U(B) был использован интерполяционный многочлен нулевой степени. Точность вычисления U(B) можно повысить, если для вычисления U(B) использовать интерполяционный многчлен первой степени. Для построения такого многочлена , кроме точки М, используем внутренний узел А, ближайший к узлу В по направлению оси 0х (рис. 7.4):

у

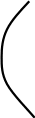
М В А

h

Г

0. х

Рис. 7.4

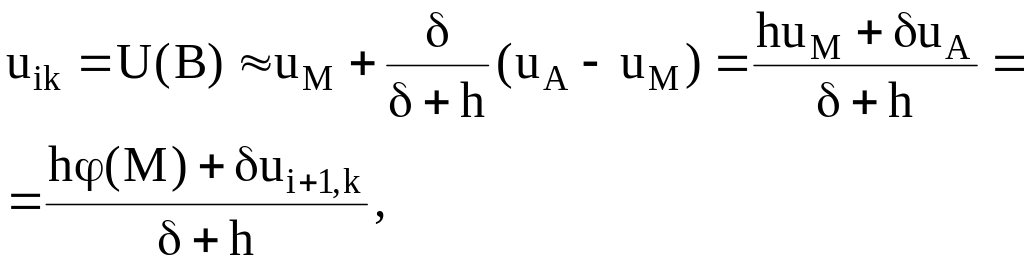(7.12)

где .

Погрешность замены (7.12) имеет порядок h².

7.5. Итерационный метод решения системы

конечно – разностных уравнений

Выше было сказано, что для получения приближенного решения краевой задачи требуется решить систему конечно – разностных уравнений. Если число узлов сетки велико, то непосредственное решение системы становится затруднительным. На практике для решения систем конечно – разностных уравнений удобно применять итерационные методы.

Рассмотрим краевую задачу для уравнения Лапласа (7.8). Конечноразностные уравнения строим для квадратной сетки (7.10). Выбираем начальные приближения для всех внутренних узлов сетки. Для граничных узлов сетки начальные приближения вычисляем по формуле (7.7):

,

где М – ближайшая к рассматриваемому граничному узлу точка границы Г в направлении оси 0х.

Следующие приближения для внутренних узлов сетки вычисляем по формуле

. (7.13)

Следующие приближения для граничных узлов сетки вычисляем по формуле

(7.14)

где А – внутренний узел сетки, ближайший к рассматриваемому граничному узлу по направлению оси 0х.

Для получения начальных приближений для внутренних узлов сетки можно указать два способа:

1. значения во внутренних узлах получают путем интерполяции, использующей известные граничные значения;

2. грубо решают краевую задачу с помощью крупной сетки, а затем, используя полученные значения и интерполирование, вы числяют для данной мелкой сетки.

Рассмотренный метод называется методом Либмана.

Доказано, что для любого шага сетки h метод Либмана сходится к точному решению независимо от выбора начальных значений, причем погрешность приближенного решения имеет порядок h². На практике для оценки погрешности полученных результатов часто поступают следующим образом. Находят решение с шагом сетки h и с шагом сетки 2h. Сравнивают полученные значения в одинаковых узлах. Если эти значения совпадают на заданном числе знаков, то решение с шагом h принимают за ответ. Если такого совпадения нет, то шаг h делят пополам, находят решение с шагом h/2 и проводят сравнение решений с шагом h и с шагом h/2 и т.д.