6.8. Приближенное решение систем дифференциальных

уравнений и дифференциальных уравнений высших порядков

Рассмотрим систему трех дифференциальных уравнений:

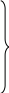
(6.39)

где х – независимая переменная;

y, z, u – искомые функции.

Требуется найти решение системы, удовлетворяющее начальным условиям

. (6.40)

Обозначим

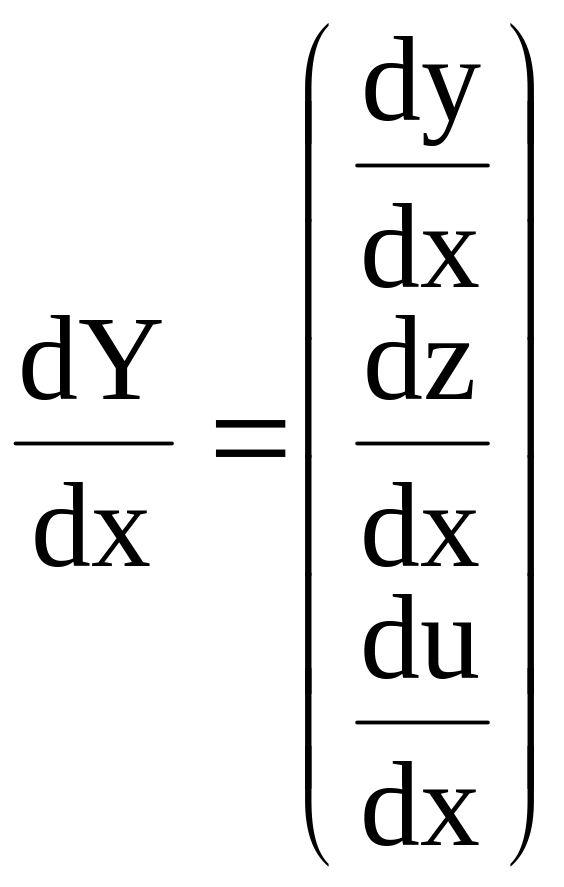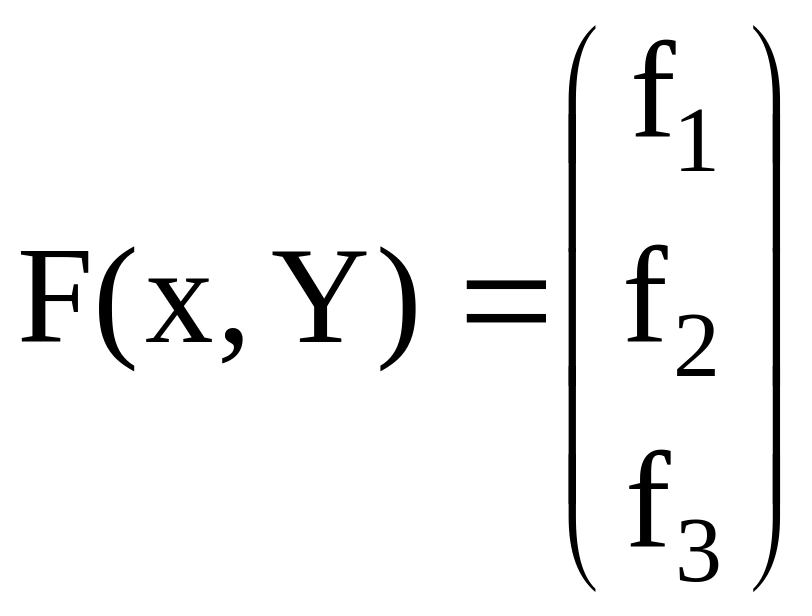; . (6.41)

После введения новых обозначений система (6.39) запишется в виде

, (6.42)

а начальные условия (6.40) – в виде

. (6.43)

Все рассмотренные выше численные методы решения задачи Коши для дифференциального уравнения первого порядка переносятся без изменений на случай системы уравнений. Формальное отличие состоит лишь в том, что в соответствующих соотношениях вместо скалярных величин у, у₀, f(x,y) участвуют векторные величины Y, Y₀, F(x,Y). Например, расчетная формула метода Эйлера для решения заданной системы (6.42) с начальным условием (6.43) запишется в виде

. (6.44)

где .

В развернутом виде формула (6.44) запишется следующим образом:

(6.45)

аналогично поступают и при решении системы другими методами. Например, расчетная формула метода Рунге – Кутта имеет следующий вид:

) ,

где

В развернутом виде каждое из этих соотношений запишется в виде трех соотношений для скалярных величин.

Таким образом между решением одного дифференциального уравнения первого порядка и решением системы дифференциальных уравнений имеется лишь часто количественное различие – число требуемых вычислений растет пропорционально числу неизвестных функций.

П ример. Применяя метод Эйлера, найти приближенное решение системы дифференциальных уравнений

с начальными условиями

у(0)=0; z(0)=-1

на отрезке [0, 0.3] с шагом y=0.1. Вычисления оформить в виде табл. 6.3.

Таблица 6.3

0	0	0 -1	1 0	0.1 0
1	0.1	0.1 -1	1.2 0.4	0.12 0.04
2	0.2	0.22 -0.96	1.4 0.8	0.14 0.08
3	0.3	0.36 -0.88

Приближенное решение системы в последовательных точках находим по формуле (6.44):

;

, т.е.

, т.е.

, т.е.

Отметим, что решением данной системы являются функции . Сравним полученные приближения Y₁, Y₂, Y₃ с точными:

; .

Рассмотрим дифференциальное уравнение n-го порядка

с начальными условиями

; ; .

Обозначим

; ; …; .

В этом случае вместо заданного дифференциального уравнения можно рассматривать эквивалентную систему дифференциальных уравнений:

……………….

с начальными условиями

; ; ; .

Таким образом, дифференциальные уравнения высших порядков могут быть сведены к системе дифференциальных уравнений первого порядка. Поэтому на них распространяются все вышерассмотренные методы. Кроме этого, существуют методы, разработанные специально для решения дифференциальных уравнений высших порядков.