3. . Интерполяционный многочлен Лагранжа

Пусть задана функция f(x) в (n+1) узле интерполяции:

x	x0	x1	…	xn
f(x)	f(x0)	f(x1)	…	f(xn)

Показано, что интерполяционный многочлен существует, притом единственный. Необходимо его построить.

П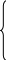 остроим вспомогательный многочлен , равный единице при и равный нулю в остальных узлах интерполяции, т.е.

1 при

(1.3)

0 при

Так как все узлы интерполяции, кроме , являются корнями многочлена , последний можно записать в виде

. (1.4)

Постоянную с определяем из условия подстановкой в (1.4):

.

Таким образом,

. (1.5)

Рассмотрим многочлен

(1.6)

Покажем, что это интерполяционный многочлен. Действительно, , как линейная комбинация с постоянными коэффициентами многочлена степени n, является многочленом степени, не выше n, причем

.

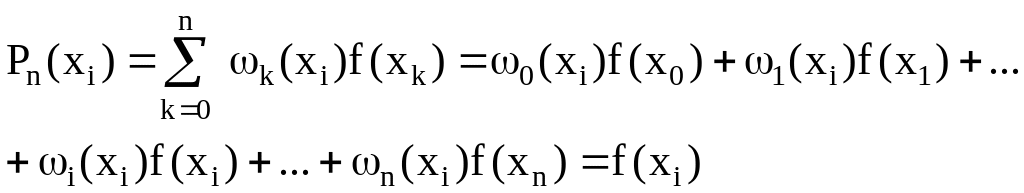Интерполяционный многочлен , получаемый по формуле (1.6), называется интерполяционным многочленом Лагранжа (Ж. Лагранж (1736 – 1813) – великий французский математик и механик), а само равенство (1.6) – формулой Лагранжа. Применяется и другая форма записи интерполяционного многочлена Лагранжа.

Введем - многочлен степени (n+1):

.

При помощи многочлен запишется в виде

.

Интерполяционный многочлен можно представить в следующем виде:

(1.7)

Пример. Построить интерполяционный многочлен Лагранжа для функции, заданной таблично:

X	-0.5	0	1
f(x)	-0.21	-1.50	0.53

.

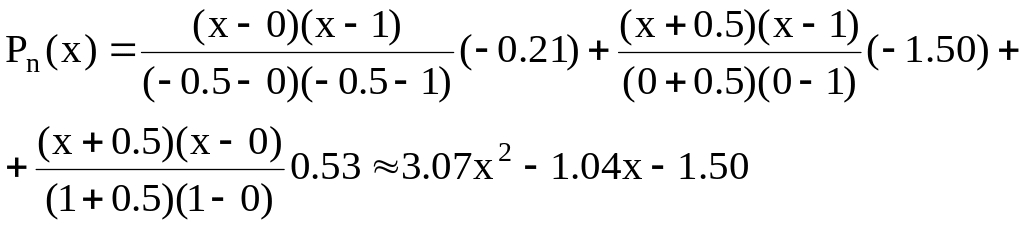Отметим, что в формулах (1.6) и (1.7) в слагаемых суммы множителя зависят только от выбора узлов x_i и от точки х и не зависят от функции f(x). Множители f(x_k) позволяют учитывать влияние на свойств функции и ее значений. Это особенно удобно в тех случаях, когда необходимо составлять интерполяционные многочлены для различных функций по одной системе узлов . Множители можно посчитать один раз и использовать их при составлении всех интерполяционных многочленов.

Неудобство интерполяционной формулы Лагранжа проявляется в следующей ситуации. Пусть составили интерполяционный многочлен по m узлам. После проверки результата оказалось, что точность недостаточна. В этом случае на практике часто строят интерполяционный многочлен, добавив один или несколько новых узлов. Вычисления, которые проводились с учетом m узлов, окажутся абсолютно непригодными в этом случае, все вычисления необходимо проводить с самого начала, так как в интерполяционном многочлене Лагранжа меняются все слагаемые.

1.4. Погрешность интерполяционной формулы Лагранжа

Пусть для функции f(x), заданной в (n+1) узле, построили интерполяционный многочлен Лагранжа . Значения заданной функции и интерполяционного многочлена в узлах интерполяции сов падают. Нас интересует, насколько близко построенный многочлен

приближается к функции f(x) в других точках отрезка [a,b], содержащего узлы интерполяции, т.е. насколько велика погрешность интерполирования

при .

Пусть заданная функция f(x) есть многочлен степени, не выше n. Тогда является также многочленом степени не выше n. Интерполяционный многочлен и заданная функции в (n+1) узле имеют одинаковые значения, следовательно, имеет по крайней мере (n+1) корень. Многочлен степени n не может иметь больше n корней. Следовательно, =0, и совпадает с f(x) во всех точках отрезка. Во всех остальных случаях .

Теорема. Пусть интерполируемая функция f(x) имеет на отрезке, [a b], содержащем узлы интерполяции , непрерывные производные до порядка (n+1). Тогда на [a,b] существует такая точка , что для погрешности интерполирования будет верно равенство

.

Доказательство. Рассмотрим вспомогательную функцию

, (1.8)

где к – некоторая константа.

Очевидно, что . Подберем k таким, чтобы , где х – та точка отрезка [a,b], для которой строим интерполяционный многочлен и производим оценку погрешности интерполирования. Подставляя в (1.8) z=x и , получаем

. (1.9)

Знаменатель этой дроби отличен от нуля, так как . Итак, функция на отрезке [a,b] имеет (n+2) корня:

х₀, х₁, …,х_n, х.

Применяя теорему Ролля к функции , получим, что имеет по крайней мере (n+1) корень на интервале [a,b]. Применяем теорему Ролля к функции . Получаем, что имеет по крайней мере n корней на интервале [a,b]. Продолжая эти рассуждения, придем к выводу, что имеет по крайней мере один корень на интервале [a,b], т.е. существует такая точка на интервале [a,b], что .

Вычисляем (n+1) производную от функции :

. (1.10)

Подставляя в (1.10) и , получаем

,

откуда

. (1.11)

Из формул (1.9) и (1.11) получаем

.

Отсюда

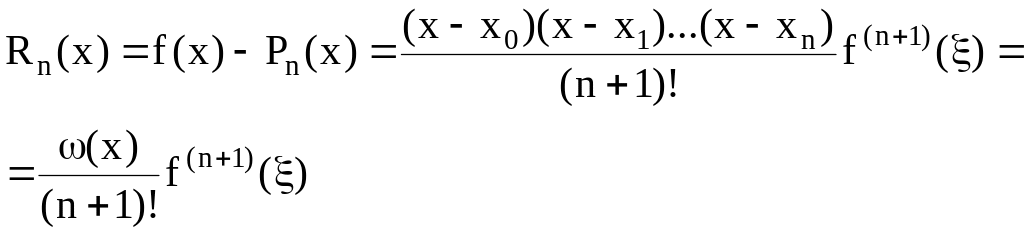(1.12)

Теорема доказана.

Обозначая

,

получаем

. (1.13)

Рассмотрим следующую задачу.

На отрезке [a,b] известны значения функции f(x) в m точках . Требуется построить интерполяционный многочлен для приближенного вычисления функции в некоторой точке х. Для построения необходимо взять (n+1) узел. Какие точки взять в качестве узлов интерполяции, чтобы погрешность была наименьшей? Рассмотрим неравенство (1.13). Множитель не зависит от выбора узлов интерполяции. Множитель принимает наименьшее значение, если узлы интерполяции выбираются следующим образом. В качестве х₀ возьмем ближайшую к х из заданных точек, в качестве х₁ – ближайшую к х из оставшихся заданных точек и т.п.

Очевидно, что при таком выборе узлов принимает наименьшее значение.

Пример. Оценить, с какой точностью можно вычислить по интерполяционной формуле Лагранжа , если восспользоваться известными величинами , , .

Рассмотрим функцию . Узлы интерполяции: х₀=25; х₁=36; х₂=49. По этим узлам можно построить . Погрешность

;

; ; ;

;

Итак, рассмотрены интерполяционная формула Лагранжа и ее погрешность. Отметим, что при составлении интерполяционного многочлена Лагранжа никаких условий на расстояния между узлами интерполяции не ставилось: они могут быть произвольными, не равными между собой. Естественно ожидать, что, если расстояния между последовательными узлами интерполяции равны, вид интерполяционного многочлена упростится. Для записи интерполяционных многочленов в этих случаях требуется понятие о конечных разностях.