6.2. Решение дифференциальных уравнений

с помощью рядов Тейлора

Предположим, что процесс решения задачи (6.1), (6.2) доведен до некоторой точки и известно (точно или приближенно) соответствующее значение искомого решения в очередной точке сетки:

.

Напишем разложение функции y(x) в ряд Тейлора в окрестности точки ;

Подставляя в полученное разложение x =x_n+1 и обозначая y^(j)(x_n)=y_n^(j), получим

. (6.6)

Отсюда

. (6.7)

Нахождение решения с помощью ряда Тейлора является одношаговым методом, так как для вычисления у_n+1 требуется информация только об одной предыдущей точке х_n, y_n.

Если решение уравнения (6.1) имеет на отрезке непрерывную производную порядка (m+1), погрешность приближенного равенства (6.7) будет величиной порядка . При достаточно малых h и больших m погрешность будет величиной достаточно малой. Для применения формулы (6.7) необходимо вычислить производные, входящие в правую часть формулы. Исходное уравнение записывается в виде

.

Отсюда

. (6.8)

Дифференцируя заданное уравнение по х, получим

. (6.9)

Отсюда

, (6.10)

где значения функции f(x,y) и ее производных вычисляются при x=x_n , y=y_n .

Дифференцируя (6.9) по х и подставляя сюда x=x_n , y=y_n , получим

(6.11)

где значения функции f(x,y) и ее производных вычисляются при x=x_n , y=y_n .

Очевидно, что с ростом порядка производных выражения для их вычисления становятся все более громоздкими, поэтому при m>1 формула (6.7) редко применяется на практике. При использовании ЭВМ применение этого метода требует написания большого числа блоков вычисления производных, что приводит к большим затратам машинного времени. На практике в основном применяются методы, не требующие нахождения значений производных от правых частей уравнений.

Таким образом, с точки зрения практических вычислений этот метод обычно неудобен. Однако при сравнении различных практически применяемых методов для их оценки есть некоторый критерий – насколько тот или иной метод согласуется с разложением в ряд Тейлора. Подставляя в (6.6) выражения для , , (формулы (6.8), (6.10), (6.11)), получим

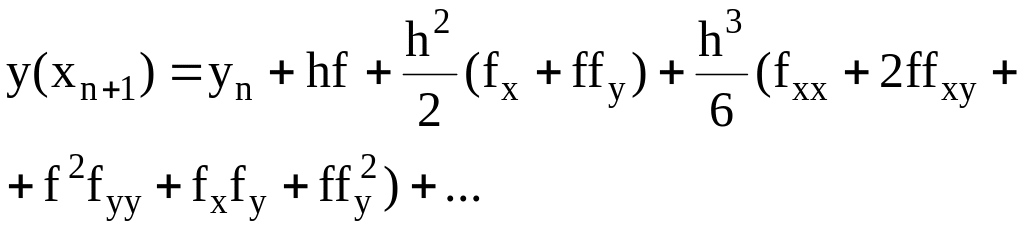, (6.12)

где значения функции f(x,y) и ее производных вычисляются при x=x_n , y=y_n .

6.3. Метод Эйлера Пусть дано дифференциальное уравнение

с начальным условием

.

Выбрав достаточно малый шаг h, строим последовательность равноотстоящих точек . Заменим интегральную кривую на отрезке [x₀, x₁] отрезком прямой, проходящей через точку и имеющей угловой коэффициент :

.

Подставляя в уравнение прямой х=х₁, получаем

.

Производим аналогичное вычисление на частном отрезке [x₁, x₂]. Получаем

.

Продолжая этот процесс, получаем формулу

. (6.13)

Это и есть расчетная формула метода Эйлера. Метод Эйлера, как видно из формулы (6.13), - одношаговый метод. В результате применения метода Эйлера интегральная кривая заменяется ломаной линией с вершинами в точках , , … . Первое звено линии касается истинной интегральной кривой в точке (рис. 6.1).

y

M₁ M₂ M₃

Y=f(x)

M₀

0 х₀ х₁ х₂ х₃ x

Рис. 6.1

Оценим погрешность метода Эйлера на одном шаге. Сравним (6.12) и (6.13).Найденное при помощи метода Эйлера приближенное решение совпадает с разложением в ряд Тейлора вплоть до членов порядка h. Следовательно, погрешность метода Эйлера на одном шаге есть величина порядка h².

Метод Эйлера – один из самых старых и широко известных методов численного решения дифференциальных уравнений. Его недостатки:

1. малая точность;

2. систематическое накопление ошибок.

Поэтому метод Эйлера применяется в основном для ориентировочных расчетов.