3.7. Метод итерации (метод последовательных приближений)

Пусть дано уравнение f(x)=0, (3.6)

где f(x) – непрерывная функция.

Требуется вычислить действительный корень уравнения (3.6), находящийся на отрезке . Сущность метода итерации заключается в следующем.

Заменим уравнение (3.6) равносильным ему уравнением

, (3.7)

где - некоторая непрерывная на отрезке функция.

выбираем произвольное и подставляем его в правую часть равенства (3.7). Получаем

.

Аналогично получаем

;

:

………………..

:

………………..

Рассмотрим последовательность х₀, х₁, …, х_n, … . Пусть эта последовательность сходится, т.е. существует .

Покажем, что с является корнем уравнения (3.7). По построению , причем - непрерывная функция. Переходя в этом равенстве к пределу при , получаем

,

что и требовалось доказать.

Так как уравнения (3.6) и (3.7) равносильны, то с является корнем также исходного уравнения (3.6). Выясним, при каких условиях итерационный процесс сходится.

a0=1; b0=2	bn	0,4286	0,1088
	an	-0,3333	-0,1154
	f ’(bn)	14	9,4082
f ’(x)=3x2+2>0 f ’’(x)=6x>0 при 1x2	f(bn)-f(an)	9	1,9863
	f(bn)	6	1,0233
	f(an)	-3	-0,9630
f(x)=x3+2x-6 f(1)= -3; f(2)=6	bn-an	1	0,2381	0,0139
	bn	2	1,5714	1,4626
	an	1	1,3333	1,4487
	n	0	1	2

Ответ:

Теорема. Пусть функция определена и дифференцируемана отрезке [a,b], причем все ее значения . Пусть кроме этого,

при .

Тогда итерационный процесс сходится и дает в пределе единственный корень уравнения .

Доказательство. Уравнение имеет на отрезке [a,b] действительный корень. Обозначим его .

Выбираем произвольное х₀ [a,b] и строим итерационную последовательность , ,…, …

Рассмотрим

.

Применяем теорему Лагранжа

,

где лежит между и х, т.е. на отрезке [a,b].

Согласно неравенству (3.8) будем иметь

.

Аналогично находим

.

Используя предыдущее неравенство, получаем

.

Повторяя указанный процесс, находим, что

. (3.9)

По условию теоремы М<1. С учетом этого из неравенства (3.9) вытекает, что

,

т.е. .

Таким образом, итерационная последовательность сходится и дает в пределе корень уравнения . Корень этот единственный. Действительно, предположим, что на этом отрезке есть еще корень уравнения ₁ . Тогда

.

Пришли к противоречию.

Теорема доказана.

Замечание 1. По условию теоремы итерационный процесс сходится при любом выборе х₀ [a,b]. Благодаря этому он является самоисправляющимся, так как неверно вычисленное х_к [a,b] можно рассматривать как новое нулевое приближение.

Замечание 2.

(n=0, 1, 2,…).

у

у=х

0 х₂ х₁ х₀ х

Рис. 3.6

Таким образом, каждое последующее приближение ближе к корню, чем предыдущее.

Рассмотрим геометрический смысл метода итерации. Корень уравнения - это абсцисса точки пересечения кривой и прямой . На рис. 3.6 изображен случай .

Стрелками отмечено, как по приближению х₀ строим приближенно х₁. Аналогично строим приближения х₂, х₃, … . В этом случае последовательные приближения монотонно убывают (или монотонно возрастают при ). Условие теоремы [a,b] автоматически выполняется если [a,b].

На рис.3.7 изображен случай .

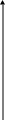
у

у=х

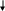
0 х₁ х₂ х₀ х

Рис.3.7

у

у=х

0 х₀ х₁ х₂ х

Рис. 3.8

Последовательные приближения х₀, х₁, … колеблются около точного значения корня, приближаясь к нему. В этом случае достаточно проверить принадлежность отрезку [a,b] приближений х₀ и х₁. Остальные приближения автоматически будут принадлежать отрезку [a,b].

На рис. 3.8 изображен случай . Итерационный процесс расходится.

Итак, для применения метода итерации уравнение f(x)=0 нужно привести к виду , так, чтобы при .

Это можно сделать различными способами. Например, уравнение f(x)=0 заменяется равносильным

.

В этом случае

.

Параметр подбираем так, чтобы

при .

Уравнение f(x)=0 можно заменить равносильным

,

где - произвольная, дифференцируемая на отрезке [a,b] функция, не имеющая на нем корней.

Функцию подбираем так, чтобы

при .

Можно показать, что при соответствующем выборе функции получаются расчетные формулы метода хорд и метода касательных, которые являются итерационными методами.

Оценка приближения

Из неравенства (3.9), учитывая, что , получаем

. (3.10)

Приведем без доказательства еще одну формулу для оценки погрешности

. (3.11)

Правые части неравенств (3.10) и (3.11) содержат множитель . Отсюда следует, что итерационный процесс сходится тем быстрее, чем меньше М. Если , погрешность удобно оценить следующим образом. Последовательные приближения х_n-1 и х_n в этом случае, как указывалось выше, лежат по разные стороны от корня , и поэтому

(3.12)

Если же за приближенное значение корня взять полусумму последних полученных приближений

,

то . (3.13)

Пример. Вычислить приближенно действительный корень уравнения . Для рассматриваемого примера:

; f(1)=-1; f(2)=7;

при всех х.

Действительный корень находится на отрезке [1, 2]. Сузим этот отрезок при помощи метода половинного деления. Вычислим f(1,5)=1,875>0. Поэтому

.

Заменяем исходное уравнение равносильным

,

получаем

; .

Находим , такое, чтобы при .

Пусть, напрмер, . Тогда

;

.

Так как при , получаем

.

Пусть =0,1.

При таком выполняется достаточное условие сходимости итерационного процесса, так как

=

Выбираем х₀=1.25.

Подставляя х₀ в правую часть уравнения

,

получаем х₁=1.229687.

Аналогично находим следующие приближения:

х₂=1.220773; х₃=1.216765; х₄=1.214944;

х₅=1.214113; х₆=1.213732; х₇=1.213558;

х₈=1.213478; х₉=1.213442;

По формуле (3.11) оценим погрешность

.

Итак, =1.2134.

Погрешность не превышает 0.0006.