
- •Глава 1. Интерполирование
- •Постановка задачи интерполирования
- •1.2. Единственность интерполяционного многочлена
- •. Интерполяционный многочлен Лагранжа
- •1.4. Погрешность интерполяционной формулы Лагранжа
- •. Конечные разности и их свойства
- •1.6. Первая интерполяционная формула Ньютона
- •1.7. Вторая интерполяционная формула Ньютона
- •1.8. Интерполяционная формула Гаусса
- •1.10. Численное дифференцирование
- •Глава 2. Численное интегрирование
- •2.1. Общие замечания
- •Глава 3. Численные методы решения алгебраических и трансцендентных уравнений
- •3.1. Вводные замечания
- •3.2. Отделение корней
- •3.3. Метод половинного деления
- •3.5. Метод Ньютона (метод касательных)
- •3.6. Комбинированный метод
- •3.7. Метод итерации (метод последовательных приближений)
- •Глава 4. Решение систем линейных уравнений
- •4.1. Метод Гаусса (схема единственного деления)
- •4.2. Вычисление определителей
- •4.3. Вычисление обратной матрицы
- •4.4. Некоторые сведения из линейной алгебры
- •Рассмотрим систему линейных алгебраических уравнений
- •Вычитая второе равенство из первого, получаем
- •4.6. Приведение линейной системы к виду,
- •4.7. Метод Зейделя Пусть система линейных алгебраических уравнений приведена к виду
- •Глава 5. Обработка результатов наблюдений
- •5.1. Постановка задачи
- •5.2. Приближение функции, заданной таблично,
- •Глава 6. Численные методы решения
- •6.1. Методы решения задачи Коши. Вводные замечания
- •6.2. Решение дифференциальных уравнений
- •6.3. Метод Эйлера Пусть дано дифференциальное уравнение
- •6.4. Уточненный метод Эйлера Рассмотрим дифференциальное уравнение
- •6.6. Методы Рунге – Кутта Пусть дано дифференциальное уравнение
- •6.7. Метод Милна
- •6.8. Приближенное решение систем дифференциальных
- •6.9.Краевые задачи для обыкновенных дифференциальных
- •6.10. Решение краевых задач
- •6.11. Метод прогонки Рассмотрим линейную систему уравнений (6.54). Преобразуя первые (n-1) уравнения:
- •Глава 7. Численное решение дифференциальных уравнений в частных производных
- •7.1. Классификация дифференциальных уравнений
- •7.2. Метод сеток решения краевых задач
- •7.3. Погрешность аппроксимации дифференциальных уравнений
- •7.4. Аппроксимация граничных условий
- •7.6. Метод сеток для уравнений
Министерство образования и науки Украины
Национальный аэрокосмический университет
им. Н.Е. Жуковского
«Харьковский авиационный институт»
Кафедра информатики
КОНСПЕКТ ЛЕКЦИЙ
«Численные методы»
Для специальностей:
7.080202 –Прикладная математика;
7.091302 – Метрология и измерительная техника;
8.080401 – Информационные управляющие системы и технологии;
8.091301 – Информационно-измерительные системы.
Харьков –2001 г.
ПРИЛОЖЕНИЯ
Примеры выполнения
лабораторных работ
В В Е Д Е Н И Е
Численные методы решения задач занимают большое место в практической деятельности инженеров. Необходимость применения численных методов возникает довольно часто. Рассмотрим простейшие примеры.
При решении прикладной задачи возникла необходимость получения решения алгебраического уравнения степени
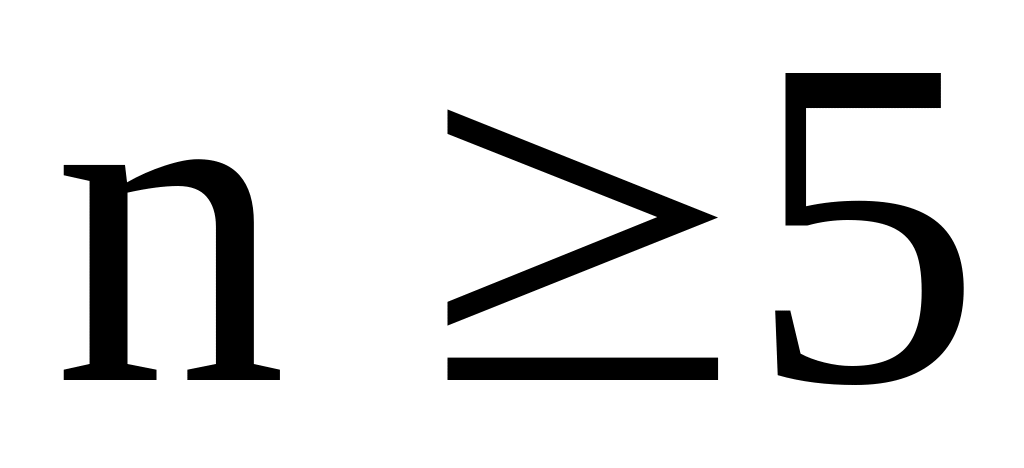 .
Норвежский математик Н. Абель доказал,
что алгебраическое уравнение n-й
степени с произвольными буквенными
коэффициентами при
неразрешимо в радикалах. Не может быть
получено точное решение и для огромного
большинства трансцендентных уравнений,
встречающихся на практике. Однако
задачу можно считать практически
решенной, если удается найти корни
уравнения с требуемой точностью при
помощи численных методов.
.
Норвежский математик Н. Абель доказал,
что алгебраическое уравнение n-й
степени с произвольными буквенными
коэффициентами при
неразрешимо в радикалах. Не может быть
получено точное решение и для огромного
большинства трансцендентных уравнений,
встречающихся на практике. Однако
задачу можно считать практически
решенной, если удается найти корни
уравнения с требуемой точностью при
помощи численных методов.При вычислении определенных интегралов часто приходится сталкиваться с функциями, для которых первообразная не выражается через элементарные функции. Кроме того, подынтегральная функция при практических расчетах может быть задана таблично, и тогда само понятие первообразной теряет смысл. В этих случаях интегрирование заменяется приближенным вычислением интеграла при помощи численных методов.
Таких примеров можно привести много. Решение задач численными методами связано с выполнением большого объема вычислительной работы. Поэтому особенно успешно и эффективно стали применяться численные методы с появлением ЭВМ. В свою очередь, развитие вычислительной техники способствовало появлению новых численных методов.
В настоящее время резко расширилась сфера приложения математики, и сейчас трудно указать область науки и техники, в которой бы не применялись ЭВМ и численные методы.
Глава 1. Интерполирование
Постановка задачи интерполирования
При решении
практических задач довольно часто
приходится иметь дело с функциями,
заданными таблично для некоторого
конечного множества значений аргумента
![]() *,
принадлежащих отрезку [a,b]
из области определения функции. В
процессе же решения задачи может
появиться необходимость использования
значений функций в точках, не совпадающих
с табличными. В этом случае строят
функцию
*,
принадлежащих отрезку [a,b]
из области определения функции. В
процессе же решения задачи может
появиться необходимость использования
значений функций в точках, не совпадающих
с табличными. В этом случае строят
функцию![]() ,
достаточно простую для вычислений,
которая в заданных точках
совпадает с табличными значениями
функции, т.е.
,
достаточно простую для вычислений,
которая в заданных точках
совпадает с табличными значениями
функции, т.е.
![]()
![]() .
.
В остальных точках
отрезка [a,b]
функция
приближенно представляет функцию f(x).
Вместо вычисления значения функции
f(x)
в произвольной точке отрезка [a,b]
вычисляют значение
в этой точке и полагают
![]() .
Задача по строения такой функции
называется задачей интерполирования.
Точки
называются узлами интерполяции (или
узлами интерполирования), а функция
- интерполирующей функцией.
.
Задача по строения такой функции
называется задачей интерполирования.
Точки
называются узлами интерполяции (или
узлами интерполирования), а функция
- интерполирующей функцией.
Интерполирование
можно использовать и в тех случаях,
когда аналитическое выражение функции
f(x)
известно, но является сложным, и вычисление
каждого значения требует большого
объема вычислительной работы. Если же
требуется вычислить значение функции
для большого количества значений
аргумента, имеет смысл вычислить
несколько значений f(xi)
![]() ,
по этим значениям построить интерполирующую
функцию и с ее помощью приближенно
вычислить значения f(x)
в остальных точках.
,
по этим значениям построить интерполирующую
функцию и с ее помощью приближенно
вычислить значения f(x)
в остальных точках.
Слово “интерполирование” означает изхождение внутренних значений. На практике могут встретиться два случая.
Требуется вычислить f(x) для
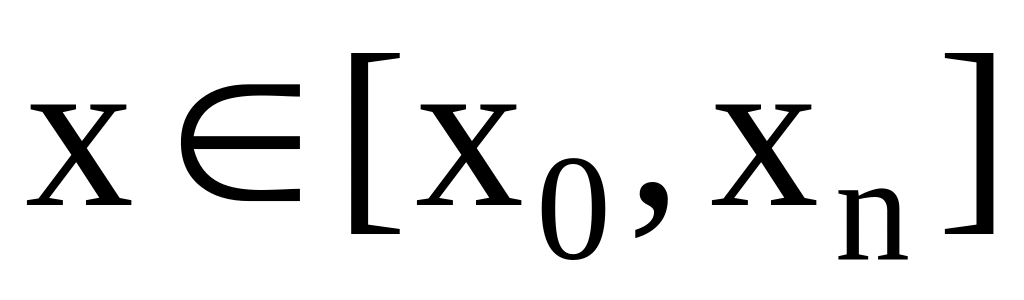 .
Задача в этом случае называется
интерполированием в узком смысле.
.
Задача в этом случае называется
интерполированием в узком смысле.Требуется вычислить f(x) для
 .
В этом случае задача называется
экстраполированием.
.
В этом случае задача называется
экстраполированием.
В дальнейшем под
интерполированием понимаем оба эти
случая. Геометрически задача
интерполирования означает построение
кривой
![]() ,
проходящей через заданные точки плоскости
с координатами
,
проходящей через заданные точки плоскости
с координатами
![]() .
Очевидно, что через данные точки можно
провести бесчисленное множество
различных кривых. Задача становится
однозначной, если интерполирующую
функцию искать в виде алгебраического
множества степени, не выше n
. Интерполирование в этом случае
называется алгебраическим. Если отрезок
[a,b],
содержащий узлы интерполяции, имеет
малую длину, а функция f(x)
имеет производные достаточно высоких
порядков, то из формулы Тейлора вытекает,
что она мало отличается от алгебраического
многочлена. Можно ожидать, что в этих
случаях алгебраическое интерполирование
даст достаточно высокую точность.
.
Очевидно, что через данные точки можно
провести бесчисленное множество
различных кривых. Задача становится
однозначной, если интерполирующую
функцию искать в виде алгебраического
множества степени, не выше n
. Интерполирование в этом случае
называется алгебраическим. Если отрезок
[a,b],
содержащий узлы интерполяции, имеет
малую длину, а функция f(x)
имеет производные достаточно высоких
порядков, то из формулы Тейлора вытекает,
что она мало отличается от алгебраического
многочлена. Можно ожидать, что в этих
случаях алгебраическое интерполирование
даст достаточно высокую точность.
На практике используют не только алгебраическое интерполирование. Если, например, на всей оси интерполируется периодическая функция, естственно искать интерполирующую функцию в виде тригонометрического многочлена с тем же периодом. Иногда в качестве интерполирующей функции удобно выбирать рациональную функцию и др.
Рассмотрим подробнее алгебраическое интерполирование.
1.2. Единственность интерполяционного многочлена
Пусть на отрезке
[a,b]
заданы узлы интерполяции
и значения функции f(x)
в этих узлах
![]() .
Все узлы предполагаются различными,
т.е.
.
Все узлы предполагаются различными,
т.е.
![]() при
при
![]() .
Требуется выяснить, существует ли
интерполяционный многочлен
.
Требуется выяснить, существует ли
интерполяционный многочлен
![]() степени, не выше n,
и является ли он единственным. Запишем
интерполяционный многочлен в виде
степени, не выше n,
и является ли он единственным. Запишем
интерполяционный многочлен в виде
![]() .
.
Так как - интерполяционный многочлен, он должен удовлетворять условиям
![]() (1.1)
(1.1)
Эти условия приводят
к системе линейных алгебраических
уравнений относительно неизвестных
![]() :
:
![]()

![]() (1.2)
(1.2)
………………………………….
![]()
Определителем этой системы является определитель Вандермонда


![]()

![]() =
=![]() .
.
В силу наших
предположений
![]() при
,
и поэтому определитель системы отличен
от нуля. Отсюда вытекает, что система
(1.2)
при
,
и поэтому определитель системы отличен
от нуля. Отсюда вытекает, что система
(1.2)
имеет единственное решение, и, следовательно, интерполяционный многочлен существует и он единственен.
