Лабораторная работа № 1 Приближенные вычисления.

Системы MathCAD 6.0⁺ и Maple VR4.

Литература: [1, введение; 2, ч.1, §1,2;3, гл.1, §1; 6, введение, гл. 1, §1; 18, ч.2, §8, п.3; 20, гл.1, §1–6].

Постановка задачи. Используя MathCAD 6.0⁺, требуется определить абсолютную или относительную погрешность искомой величины и число верных знаков.

Для этого необходимо предварительно по приложению к данному руководству (см. §6) изучить основы работы с системами MathCAD 6.0⁺ и Maple VR4 и разобрать приведенные примеры.

Приведем некоторые сведения о приближенных вычислениях.

При решении большинства практических задач можно найти лишь приближенное значение величины.

Пусть a – приближенное значение числа xR.

• Абсолютной погрешностью  приближенного числа a называется абсолютная величина разности между ним и соответствующим точным значением числа xx–a

• Предельной абсолютной погрешностью называется возможно меньшее число , удовлетворяющее неравенству x–a  

Отсюда следует, что точное число x заключено в границах a–  x  a или x  a  

Для характеристики точности замены х на а используется абсолютная погрешность, приходящаяся на единицу величины приближенного числа а.

• Относительной погрешностью числа а называется отношение абсолютной погрешности к абсолютной величине приближенного значения а числа x  

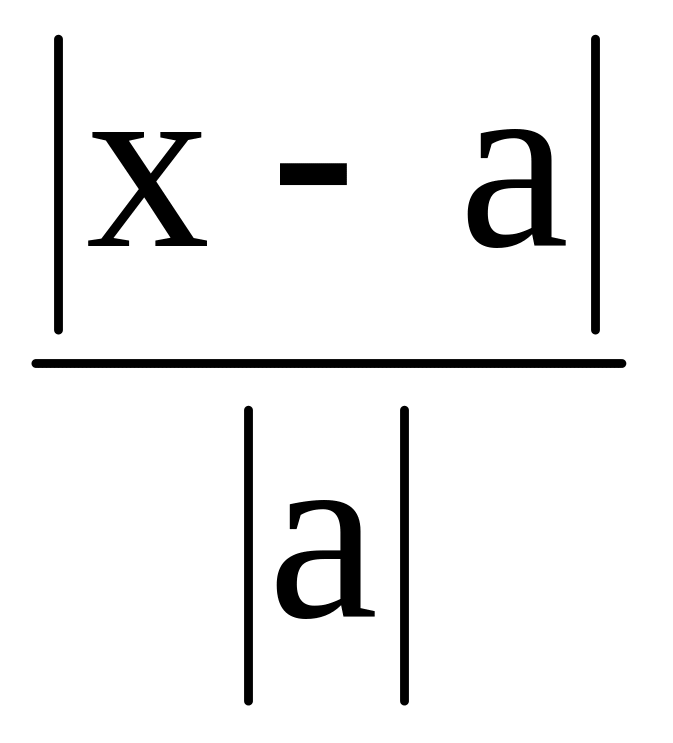
• Предельной относительной погрешностью называется возможно меньшее число  удовлетворяющее неравенству .

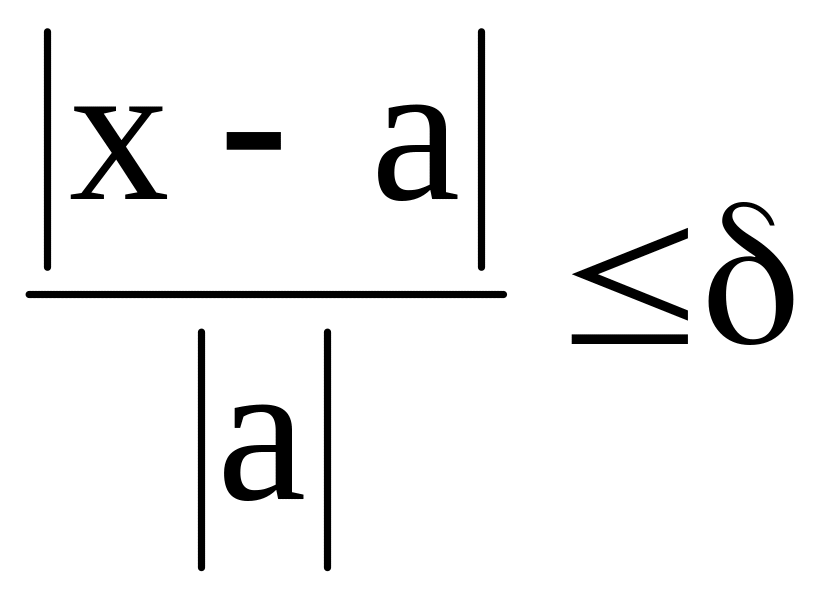Предельную относительную погрешность    принято выражать в процентах. Например, число 3,14 является приближенным значением числа . Абсолютная погрешность этого приближения равна 0,00159...; предельную абсолютную погрешность  можно считать равной 0,0016, а предельную относительную погрешность     0,000509 можно положить равной 0,00051 или в процентах   0,051

Легко видеть, что а и а   х  а 1+ или х  а 

Говорят, что n первых значащих цифр приближенного значения а числа х являются верными, если абсолютная погрешность приближенного значения числа а не превышает половины единицы n-й значащей цифры, считая разряды слева направо.

х-а  0,5  10^m-n+1,

где 10^m – вес старшего разряда числа х.

Например, для числа 121,57 число 122,00 является приближенным значением с тремя верными знаками, так как для

х121,57110² +210¹ + 110⁰ + 510^-1 + 710^-2 и m = 2, n = 3 получаем

121,57  122 0,43  0,510^2-3+1  0,5.

Если число верных знаков n1, за предельную относительную погрешность приближенного числа а с первой слева направо значащей цифрой k можно принять число

Если известно, что

, (1.1)

то приближенное значение а числа х имеет n верных знаков.

Погрешность результата арифметических действий над приближенными значениями чисел оценивается с помощью следующих правил:

1. Предельная абсолютная погрешность алгебраической суммы нескольких чисел равна сумме предельных абсолютных погрешностей слагаемых.

2. Относительная погрешность суммы положительных слагаемых не превышает наибольшей из относительных погрешностей этих слагаемых.

3. Предельная относительная погрешность произведения и частного приближенных чисел равна сумме предельных относительных погрешностей этих чисел.

4. Предельная относительная погрешность степени и корня приближенного числа равна произведению предельной относительной погрешности этого числа на показатель степени.

Пример 1.1. Вычислить , где n= 3,0567(0,0001), m = 5,72(0,02), и определить абсолютную и относительную погрешности результата.

Решение. По правилу I имеем

n-1=2,0567(0,0001);

m+n=5,72(0,02)+3,057(0,0004)=8,777(0,0204);

m-n=5,72(0,02)–3,057 (0,0004)=2,663 (0,0204).

Тогда

Используя предельные абсолютные погрешности суммы, разности и степени заданных чисел, находим соответствующие предельные относительные погрешности и по правилам III и IV получаем предельную относительную погрешность результата арифметических действий

=0,000049+0,00233+2∙0,00766=0,00238+0,01532=0,0177=1,77%.

По формуле а∙ определяем предельную абсолютную погрешность

 = 2,55∙0,0177 = 0,046.

 Ответ: А  2,55( 0,046), _A = 1,77%.

Пример 1.2. Площадь квадрата равна 25,16 см² (с точностью до 0,01см²). С какой относительной погрешностью и со сколькими верными знаками можно определить длину стороны квадрата.

Решение. Длина искомой стороны приближенно равна а =   5 (см²). Так как  = 0,01 - абсолютная погрешность площади, по формуле найдем относительную погрешность площади а₁ = 25,16 квадрата

.

Тогда в соответствии с правилом IV относительная погрешность корня приближенного числа будет равна

или  = 0,02 % .

При заданной относительной погрешности  число n верных знаков приближенного числа, равного длине стороны квадрата, определяем по формуле (1.1). Полагая первую значащую цифру k слева направо результата равной 5, решаем неравенство

. (1.2)

Откуда

, . (1.3)

Следовательно, n=3, так как 0,000240,001=10^-3 и 0,00024>0,0001=10^‑4.

Отметим, что по условию задачи длину стороны квадрата с тремя верными цифрами находить не требуется.

Решение на ПЭВМ. Загружаем MathCAD 6.0⁺(см. §6.1.1). Обозначим , . Выполняем следующие действия {a:\25.16}, {a=}.

Установим (§ 6.1.3) выводимое число знаков после запятой, равным четырем {Математика Формат числа Локальный Выводимая точность Del4OK}.

Определяем значения {d1: 0.01/25.16}, {d1=}, {d: 0.5*d1}, {d=}

Следовательно, δ=d 0.0002.

Для определения числа верных знаков длины стороны квадрата решаем неравенство из (1.2). Для этого используем команду Решить относительно переменной^*) (cм. пример 6.1.11) {0.002 Ctrl=1/2*(5+1)↑↑*0.1^n-1}. Щелкаем () на n и выбираем Решить относительно переменной из меню Символика. Окружаем результат выделяющей рамкой (↑) и используем команду округления до ближайшего меньшего целого числа floor.

И так, n=3.

Рис 1.1

Ответ: длину стороны квадрата можно определить с относительной погрешностью  = 0,02% и тремя верными знаками.

*)Убедитесь, что символьный процессор запущен.