Порядок выполнения работы

1. Получите допуск к работе.

2. Загрузите систему Maple VR4 (см. § 6.2.1).

3. Выполните примеры 6.2.1, 6.2.3, 6.2.4.

4. Запишите тексты этих примеров в тетрадь.

5. Загрузите систему MathCAD 6.0⁺ (см. § 6.1.1) и выполните те же действия, что и для системы Maple VR4.

6. Составьте алгоритм решения задачи согласно вашего варианта.

7. Решите задачу с помощью системы MathCAD 6.0⁺.

8. Текст решения с пояснениями запишите в тетрадь.

9. Составьте отчет о проделанной работе.

Содержание отчета

1. Тексты примеров применения систем Maple VR4 и MathCAD 6.0⁺ с рисунками.

2. Текст задачи на приближенные вычисления.

3. Данные для ввода в ПЭВМ.

4. Результаты расчета на ПЭВМ с подробными пояснениями к решению.

5. Интерпретация полученных данных.

Лабораторная работа № 2 Решение уравнений с одной неизвестной

Литература:[2, гл.5, §1-3; гл. 5, §2,3;6, гл. 4, §24-27; гл.IV, §1-8, гл. X, §3].

Постановка задачи. Пусть дано уравнение

f(x) = 0. (2.1)

Найти корни этого уравнения с точностью 0.

Приближенное решение уравнения (2.1) обычно разбивается на два этапа:

1. Отделение корней, т.е. установление промежутков, содержащих по одному корню.

2. Уточнение корней, т.е. сужение отрезка, содержащего корень, до такой степени, что длина отрезка становится меньше требуемой точности.

На первом этапе, как правило, применяется графический метод решения уравнений. Уточнение корней опирается на свойства непрерывных функций:

а) если функция f(x) непрерывна на отрезке [а,b] и f(x) имеет на концах этого отрезка разные знаки (f(a)f(b)<0), то на [а,b] существует хотя бы один корень уравнения (2.1);

б) если функция f(x) непрерывна и монотонна (f(x) не меняет знак на отрезке [а,b]) и f(a)f(b)<0, то на этом отрезке корень уравнения (2.1) единственный.

Рассмотрим ряд методов приближенного решения уравнения (2.1).

• Графический метод: Исходное уравнение (2.1) приводится к виду u(x)=v(x), где функции y=u(x) и y=v(x) являются простейшими элементарными и легко могут быть построены. Абсцисса x₀ точки пересечения М(x₀, y₀) графиков функций u(x) и v(x) есть искомое решение уравнения (2.1).

Точность решения невысока и определяется масштабом системы координат 0xy, в которой строятся графики функций u(x) и v(x).

Рис. 2.1

 Пример 2.1. Графическим методом решить уравнение

x³–x²–3=0 (2.2)

Решение. Уравнение (2.2) запишем в виде x³=x²+3. Обозначим u(x)=x³, v(x)=x²+3. Строим графики функций y=x³ и y=x²+3 (см. рис. 2.1). Находим абсциссу x₀ точки пересечения М этих графиков. Получаем x₀ 1.9, т.е. x₀а, b=1;2.

Сделаем проверку:

1.9³–1.9²–3=6.859–3.61–3=0.249;

1.8³–1.8²–3=5.832–3.24–3=–0.408.

Точность решения =0.1.

 Ответ: x₀ 1.9.

Пусть на этапе отделения корней установлено, что на отрезке [a,b] содержится единственный корень уравнения (2.1). Требуется найти этот корень с точностью >0.

• Метод половинного деления: Отрезок [a,b] делится пополам и выбирается та его половина, на которой функция f(x) меняет знак. Продолжая процесс половинного деления дальше, можно получить сколь угодно малый отрезок [,], содержащий корень уравнения.

Принимая за приближенное значение корня число, равное середине отрезка [,], допускаем погрешность, не превосходящую половины длины этого отрезка.

Таким образом, процесс половинного деления заканчивается при выполнении условия , где   заданная точность.

• Метод касательных (Метод Ньютона): Пусть f(x) имеет непрерывную производную f(x) на отрезке [a,b]. Возьмем произвольное значение x₀  [a,b]. В точке (x₀,f(x₀)) проведем к графику функции y=f(x) касательную y=f(x)=f(x₀)+f(x₀)(xx₀). Тогда пересечение касательной с осью Оx дает первое приближение . Аналогично для точки (x_1,f(x₁)) находим и т.д. Таким образом, получаем итерационную последовательность x_n по формуле

, n = 0,1,2, . . . . (2.3)

Обычно в качестве начального приближения x₀ выбирают тот конец отрезка [a, b], для которого выполняется условие f(x₀)f(x₀). Оценка погрешности приближенного значения корня, найденного методом Ньютона, производится с помощью неравенства

где x^* – точный корень уравнения (2.1).

• Метод итерации: Уравнение (2.1) приводим к виду

x=(x) (2.4)

Пусть известно приближенное, возможно весьма грубое, решение x₀ исходного уравнения. Последующие приближения вычисляем по формуле

x_n+1 =(x_n), n = 0,1,2, ... . (2.5)

Если итерационная последовательность x_n сходится к некоторому пределу, то этот предел есть корень исходного уравнения. Условия сходимости итерационного процесса дает следующая теорема.

Теорема 2.1. Пусть уравнение (2.4) имеет единственный корень на отрезке [a, b] и выполнены условия:

1) функция (x) определена и дифференцируема на отрезке [a,b] ;

2) все значения функции (x) при x  a,b принадлежат этому отрезку;

3) существует число (0,1) такое, что для всех xa,b имеет место неравенство (x) .

Тогда итерационная последовательность (2.5) сходится к корню уравнения (2.4) для любого x₀a,b.

За приближенное значение корня можно взять любой член итерационной последовательности x_n+1, n=0,1,2,... . При этом погрешность приближения определяется по формуле:

где x^* – точное решение уравнения (2.4), а число  определено в теореме 2.1.

Критерием остановки итерационного процесса является выполнение условия

(2.6)

где заданная точность решения уравнения.

Уравнение (2.1) можно преобразовать к виду (2.4) различными способами, например, полагая (x)=x+f(x), где некоторое число, выбираемое таким образом, чтобы выполнялись условия теоремы 2.1.

Пусть, например, на отрезке a,b, где уравнение (2.1) имеет единственный корень, функция f(x) монотонна. Предположим для определенности, что f(x) на a,b (если f(x) на a,b, то вместо уравнения (2.1) берем уравнение –f(x)=0), тогда 0mf(x)M, где M и m – наибольшее и наименьшее значение функции f(x) на a,b. В этом случае полагаем , а .

 Пример 2.2. Решить методом итерации с точностью 10^-2 уравнение (2.2) из примера 2.1.

 Решение. Из примера 2.1 следует, что единственный корень x^* уравнения (2.2) принадлежит отрезку ;. Обоснуем это аналитическими расчетами. Обозначим f(x)=x³–x²–3 . Функция f(x) непрерывна на ;. Т.к. f(1)=–3, f(2)=1, то на отрезке ;2 уравнение (2.2) имеет по крайней мере один корень. Поскольку f(x)=3x²–2x0 на ; то функция f(x) монотонна на этом отрезке и уравнение (2.2) имеет на ; единственный корень.

Заменим исходное уравнение равносильным

x=(x)=x–x³–x²–3. (2.7)

Определим  как указано выше. Поскольку на  f(x) монотонная функция, то 0<1=f(1)f(x)f(2)=8. Поэтому и  Покажем, что для уравнения

(2.8)

выполнены все условия теоремы 2.1

1) функция определена и дифференцируема на отрезке 

2) значения функции x удовлетворяют неравенству

x,

т.е. все значения функции x принадлежат отрезку 

3) производная функции x удовлетворяет неравенству

т.е. существует такое число 0,8751, что для всех x выполняется неравенство x.

Выбирая в качестве начального приближения правый конец отрезка  x₀=2, по формуле (2.5) находим приближения решения уравнения (2.8). Итерационный процесс останавливаем, если будет выполнено условие (2.6)

;

;

;

;

.

Т. к. x₄–x₃=1.8638–1.864=0.00020.0014, то итерационный процесс останавливаем. Решение уравнения (2.2) с точностью до 10^-2 равно x1.86.

 Ответ: x 1.86.

Для отделения корней в системе MathCAD 6.0⁺ удобно использовать графический метод. Определение промежутка, на котором заключены корни уравнения f(x)=0, выполняется, исходя из следующих соображений.

Пусть требуется найти приближенно вещественные корни алгебраического уравнения

а₀xⁿ+a₁x^n-1+a₂x^n-2+...+a_n=0. (2.9)

Обозначим

,

. (2.10)

Тогда все вещественные корни уравнения (2.9) расположены в отрезке

–с с, где

(2.11)

Cтроим на этом промежутке график функции

f(x)=a₀xⁿ+a₁x^n-1+...+a_n

и ось Оx : y=0. Отделяем корни уравнения (2.9). Если график не позволяет сразу отделить корни, сужаем промежуток –с с.

 Пример 2.3. Найти все корни уравнения

x⁴–2,3x³+4,1x²–2,7x–4,6=0 (2.12)

с тремя знаками после запятой.

Решение. Загружаем MathCAD 6.0⁺ (см. §6.1.1) . В нашем случае, согласно (2.9), (2.10), (2.11) при n=4 получаем для а=4,6, b=4,1

|а_n|=4,6, |a₀|=1 4.6/(4.6+4.1)=, 1+4.6/1=} (см. рис.2.2)

Отсюда с=5,6.

Следовательно, корни заданного уравнения находятся на промежутке [‑5,6;5,6].

Для отделения корней строим график функции (см. §6.1.3)

f(x):х^4Пробел–2.3*х^3Пробел +4.1*x^2Пробел –2.7*x–4.6}

Затем задаем изменение х на отрезке [‑5,6;5,6] с шагом h=0,1

x:–5.6,–5.5;5.6}.

Находим соответствующие пределы изменения f(x) 5.6^4=}.

Приближенно полагаем, что –6<х<6, -1000<f(x)<1000.

Запускаем графический процессор (см. пример 6.1.3) и размечаем пустой график как показано на рис.2.2. Чтобы сделать масштабную сетку по оси Х надо обратиться к меню Декартов график Формат X-Y оси. В пункте Число интервалов Х-оси установите 6 ОК. Здесь масштаб равен 2.

Видим, что график функции f(x) практически сливается с осью Ох, и корни расположены примерно на промежутке от 2 до 3. Поэтому для большей точности отделения корней сужаем промежуток изменения х до [‑3;3] и строим график f(x) при –10<f(x)<20. На этом графике масштаб равен единице.

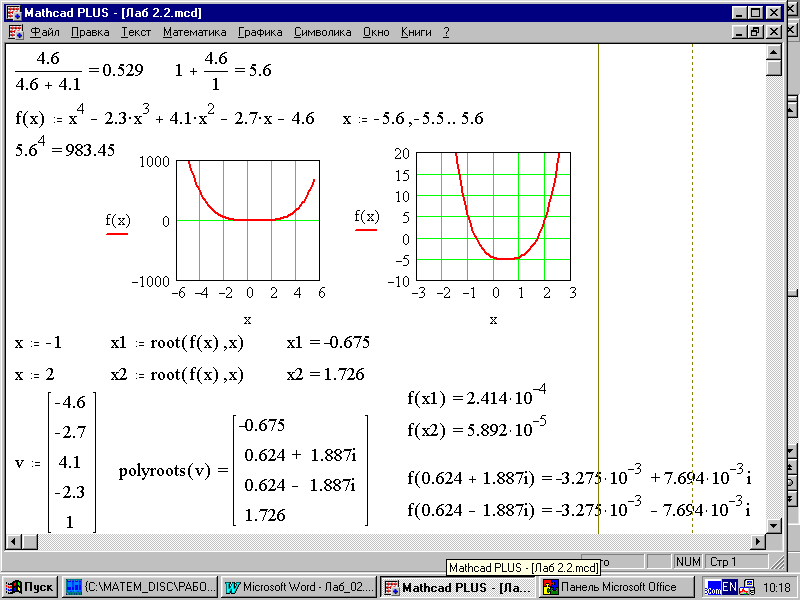
Рис. 2.2

На рис.2.2 видим, что один корень находится около точки х=‑1, второй около х=2.

Для отыскания корней используем функцию root (см. Пример 6.1.11)

{x:‑1}, {x1: root(f(x),x)}, {x1=}.

Получаем приближенное значение первого корня х1=‑0,675.

Аналогично находим второй корень х2=1,726.

{x:2}, {x2: root(f(x),x)}, {x2=}.

Делаем проверку {f(x1)=}, {f(x2)=}.

! Замечание. Если требуется получить значения корней с большим числом знаков после запятой, измените формат числа.

Графический метод помогает отделить действительные корни уравнения. Уравнение (2.12) имеет два таких корня. Чтобы найти все n-корней уравнения n-ной степени, нужно использовать функцию polyroots, которая не требует задания начальных приближенных корней, или воспользоваться командой Решить относительно переменной (см. Пример 6.1.13).

Для задания функции polyroots необходимо создать вектор v, содержащий все коэффициенты заданного уравнения, в том числе равные нулю. Определяем матрицу v размерности 51 (см. Пример 6.1.4).

{v:МатематикаМатрицыСтрок5Столбцов1Создать}.

Заполнение пустых полей начинаем сверху и вводим константу –4,6.

{–4.6TabTab–2.7TabTab 4.1Tab–2.3TabTab1}.

Затем вводим {polyroots(v)=}.

Проверяем комплексные корни.

{f(0.624+1.887i)=ПробелПробелПробел f(0.624–1.887i)=}.

Итак, все корни заданного уравнения найдены

 Ответ: х₁=–0,675, х₂=1.726, х₃=0.624+1.887i, х₄=0.624–1.887i.

Функции системы MathCAD 6.0⁺ могут быть использованы для решения задач на экстремум.

Пусть требуется решить задачу раскроя железного листа под ящик заданного или максимального объема. Ящик делается из тонкого листа с длиной l и шириной s отгибом под прямым углом полосок с шириной x (высота ящика) со всех четырех сторон.

 Пример 2.4. Дан железный лист длиной 4 м и шириной 2 м. Определить с точностью 10^-3:

а) размеры ящика объемом 1м³;

б) размеры ящика максимального объема.

 Решение. Обозначим: l=4м; s=2м; v₀=1м³; x – высота ящика; y=l–2x – длина ящика; z=s–2x - ширина ящика.

Тогда для отыскания размера отгиба такого, чтобы объем v(x) ящика был равен v₀=1м³, составляем уравнение v(x)=v₀ или v(x)–v₀=0.

Как известно, объем v параллелепипеда вычисляется по формуле , где х – высота, у – длина, z – ширина параллелепипеда.

По условию задачи: длина l=4м, ширина s=2м, заданный объем v₀=1м³. Если с каждой стороны листа отогнуть полоску (высота ящика) шириной х, то размеры ящика будут некоторыми функциями от х: х – высота, y=l–2x – длина, z=s–2x – ширина ящика. Объем в этом случае будет функцией одной переменной

v=v(x)= .

Таким образом математической моделью данной задачи является уравнение третьей степени относительно х. Высоту х надо подобрать так, чтобы v=v₀=1м³. Очевидно, что уравнение v(x)=v₀ или v(x)–v₀=0 имеет три корня, и из них надо выбрать тот, который удовлетворяет условию задачи.

Определим допустимые значения х. С одной стороны, из физических соображений, х должно быть положительным (x>0), т.к. при данная задача не имеет решения. С другой стороны, величина отгиба х ограничена заданными размерами листа. Так как меньшим размером железного листа является ширина s, то отогнуть под прямым углом с двух сторон можно полоски шириной, меньшей . Итак, допустимые значения х заключены в интервале .

! Замечание. Если х= , задача также не имеет решения. Студенту рекомендуется самостоятельно сделать из листа выкройку для ящика и теоретически определить приближенное значение х.

 Решение на ПЭВМ. Сделаем вычислительную модель поставленной задачи в MathCAD 6.0⁺ (см. §6.1.1).

Вводим следующие величины:

{♦l:4 }, {♦s:2 }, {♦v0:1 }, {♦y(x):l–2*x } – длина ящика,

{♦z(x): s–2*x } – ширина ящика,

{v(x):x*y(x)*z(x) } – объем ящика,

{♦f(x): v(x)–v0 } – заданный объем ящика. 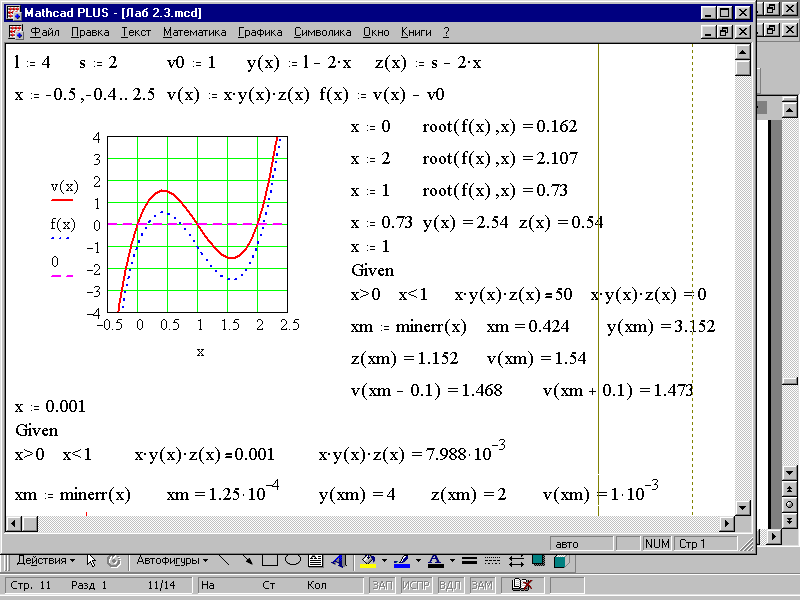Отделяем корни графическим методом (см. пример2.3). Пусть х меняется от –0.5 до 2.5 {♦x: -0.5, -0.4; 2.5 }. Строим графики функций y=v(x), y=f(x), y=0 (см. §6.1.4). Разметку пустого поля графика делаем как на рис. 2.3.

Рис.2.3

Очевидно, что уравнение f(x)=0, график которого ниже, имеет три корня: вблизи х=0, вблизи х=1 и вблизи х=2.

С помощью функции root находим соответствующие значения х (см. рис. 2.3):

{♦x:0 }, {♦root(f(x),x)=} – плоский ящик,

{♦x:1 }, {♦root(f(x),x)=} – глубокий ящик,

{♦x:2 }, {♦root(f(x),x)=} – корень не реален физически, т.к.

Таким образом x=0.73(м).

Определяем остальные размеры ящика

x:=0.73 y(x)=2.54(м) z(x)=0.54(м).

Для нахождения размеров ящика, имеющего максимально возможный для заданного листа с размерами ls объем, воспользуемся функцией Minerr(x) (см. §6.1.3), определяющей приближенное решение x заданного уравнения с минимальной среднеквадратической погрешностью.

Пусть xm – высота ящика максимального объема. Последовательно вводим: ключевое слово {♦Given }, ограничения на х {x>0 },{x<1 },решаемое уравнение {♦x*y(x)*z(x)Ctrl=50 }, задав величину объема, заведомо превышающую требуемую и вычисляем оптимальное значение х {♦xm: Minerr(x) }, {♦xm=}.

Отсюда xm=0.424(м). В самом деле, на графике функции y=v(x) (верхний график) видно, что в точке х=0.42 функция v(x) имеет локальный максимум на (0;1), равный {♦v(xm)=}. Соответственно, {♦y(xm)=}, {♦z(xm)=}.

Сделаем проверку.

{♦v(xm-0.1)=}, {♦v(xm+0.1)=}.

Очевидно, что найденные значения объема меньше v(xm).

Найдем размеры ящика минимального объема (v(x)>0) для заданного листа ls=42 (см. рис. 2.3).

{x:=0.001},

{Given}

{x>0} {x<1} – ограничение на х.

{x*y(x)*z(x)Ctrl=0.001}, {xm:=Minerr(x)}

xm=1.2510^-4 y(xm)=4 z(xm)=2 v(xm)=110^-3

Документ с решением примера 2.4 представлен на рис. 2.3.

 Ответ: a) x=0.73(м), y=2.54(м), z=0.54(м);

б) xm=0.424(м), ym=3.152(м), zm=1.152(м).

Контрольные вопросы

1. Перечислите различные методы решения уравнения с одной неизвестной. Дайте их краткую характеристику.

2. Какие свойства функции и как используются в приближенных методах решения уравнения f(x)=0?

3. Как строится итерационная последовательность?

4. Каковы достаточные условия сходимости итерационной последовательности?

5. Как аналитически определить промежуток, на котором находятся корни уравнения f(x)=0?

6. Оценка погрешности различных методов решения.