Контрольные вопросы

1. Квадратурные формулы. Принцип их получения.

2. Формулы прямоугольников, трапеций, Симпсона.

3. Оценка погрешностей квадратурных формул. Метод двойного пересчета.

4. Сравнение квадратурных формул.

5. Применение определенного интеграла в математике и физике.

6. Вычисление определенного интеграла в системах MathCAD 6.0⁺и Maple VR4.

Задание к лабораторной работе № 3

1. Сосуд имеет форму полусферы радиусом R=1м. Он заполнен жидкостью с плотностью r=0,9 кг/л. Вычислить работу, которую нужно произвести, чтобы выкачать жидкость из сосуда. Определить, насколько уменьшится уровень жидкости, если будет произведена 1/5 часть всей работы.

! Указание. Уравнение сферы: x² + y² + z²=R².

2. Бак имеет форму параболоида вращения. Радиус основания R=1м, глубина H=4м. Он заполнен жидкостью с плотностью r=0.7 кг/л. Вычислить работу, которую нужно произвести, чтобы выкачать жидкость из бака. Определить, на сколько уменьшится уровень жидкости, если будет произведена 1/3 часть работы.

! Указание. Уравнение параболоида вращения: x²+y² =2pz.

3. Кривая задана уравнением y=x² +e^-4x+sin²x+1, £ x£4. Найти длину этой кривой и координаты точек, делящих кривую на три равные части. Построить график .

! Указание. Длина дуги плоской кривой вычисляется по формуле

L= ∙dx

4. Скорость тела при торможении дается формулой u = 30( – 2)t м/мин. Определить скорость тела в тот момент, когда пройдена половина тормозного пути. Построить график.

5. Скорость самолета при разгоне дается формулой u=30( 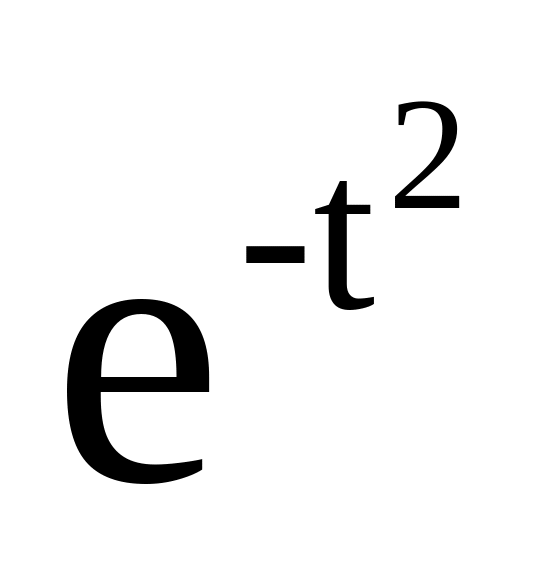+t‑1)км/час. Отрыв от Земли происходит при скорости 24 км/час. Определить, за какое время самолет преодолеет 2/3 дистанции разбега. Построить график.

6. Тело получено вращением кривой y=x²+sin²x+1, 0 £ x £ 3 вокруг оси абсцисс. Определить место вертикального распила, перпендикулярного оси абсцисс, делящего тело в отношении 1:3.

! Указание. Объем тела вращения вычисляется по формуле

V_x = p dx .

7. Кривая задана уравнением y=sin x + arctg x + x²,  £ x £ 4. Определить длину кривой и координаты точки на кривой, которая делит эту длину в отношении 1:4 (см. указание к задаче 3). Построить график.

8. Плоская фигура ограничена линиями y= , y=x² +1, x=4. Определить место разреза, делящего фигуру в отношении 2:1. Построить график.

! Указание. Площадь плоской фигуры, ограниченной сверху кривой y=f(x), вычисляется по формуле

S= dx .

9. Кривая задана уравнением y=x² + +3cos²x+3, 0£ x £ 4. Найти площадь поверхности, образованной при вращении этой кривой вокруг оси Ox и уравнения плоскостей, перпендикулярных оси Ox и делящих поверхность вращения на три части равной площади.

! Указание. Площадь поверхности вращения вычисляется по формуле

S_x =2p dx.

10. Кривая, заданная уравнением y= +3cos²x+1, 0 £ x £ 4, вращается относительно оси Ox. Найти объем тела вращения и уравнение плоскости, перпендикулярной оси Ox и делящей этот объем пополам (см. указание к задаче 6).

Порядок выполнения работы

1. Получить допуск к работе.

2. Построить математическую модель задачи.

3. Свести задачу к вычислению интегралов.

4. Подготовить данные для ввода в ПЭВМ.

5. Получить решение задачи посредством функции вычисления определенного интеграла и функции root.

6. Оценить погрешность расчетов .

7. Составить отчет.

Содержание отчета

1. Текст задачи.

2. Формулировка математической модели.

3. Данные ввода в ПЭВМ.

4. Результаты счета на ПЭВМ.

5. Графическая иллюстрация результатов.

6. Интерпретация полученных результатов.

Лабораторная работа № 4

Решение обыкновенных дифференциальных уравнений и систем операционным методом

Постановка и решение задачи

Решение обыкновенных дифференциальных уравнений и систем операционным методом основано на применении преобразования функции F(t) действительного переменного t  R в функцию F(p) комплексной переменной pC с помощью выражения:

F(p)= (4.1)

 Определение 4.1. Функция F(p) комплексной переменной p, получаемая с помощью (4.1), называется преобразованием Лапласа функции f(t), t  R. Функция F(p) называется изображением для f(t).

 Определение 4.2. Функция f(t), t  R называется оригиналом, если соответствует следующим требованиям:

1. f(t)  0 при t  0,

2. f(t)  Me^t при t  0 , где М и  - некоторые числа ,

3. f (t) на любом конечном отрезке О,Т имеет не более чем конечное число точек разрыва  рода, причем lim f(t)  f(0), t0+0

 Определение 4.3. Интеграл в правой части (4.1) называется интегралом Лапласа.

 Теорема 4.1: Если функция f(t) является оригиналом, то интеграл Лапласа сходится абсолютно и равномерно во всей полуплоскости Re p₀ ₀ , где ₀inf₀.

! Замечание 4.1: Интеграл Лапласа обозначают специальным символом “L”, поэтому изображение функции f(t) можно записать в виде F(p)=Lf(t); для обозначения соответствия между оригиналом f(t) и его изображением F(p) используют также символ “ “, тогда записывают F(p) f(t).

! Замечание 4.2: Для перехода от оригинала f(t) к его изображению F(p) и обратно используют свойства преобразования Лапласа и специальную таблицу оригиналов и изображений, вычисленных с помощью (4.1) (см. табл.4.1)

Рассмотрим применение преобразования Лапласа (4.1) к решению линейного дифференциального уравнения n-ого порядка с постоянными коэффициентами:

x⁽ⁿ⁾ + a₁ x^(n-1) + ... + a_n x=f(t) (4.2)

при начальных условиях

x(0)=x₀, x'(0)=x'₀, ... , x^(n-1)(0)=x₀^(n-1) . (4.3)

Искомое решение x(t) получим в следующем порядке:

1) к обеим частям уравнения (4.2) применим преобразование Лапласа (4.1) и перейдем от дифференциального уравнения (4.2) с начальными условиями (4.3) к линейному алгебраическому уравнению относительно неизвестного изображения Х(p) решения x(t):

(pⁿ + a₁ p^n-1 + ... + a_n-1 p + a_n ) X(p) + Q(p) = F(p) . (4.4)

Если x₀=x₀=...=x₀^(n-1) =0, то Q(p)=0.

Таблица 4.1

f(t)	F(p)	f(t)	F(p)
1. h(t)=		11.  at
2.		12. sh at
3. e at		13. ch at
4. tn e at		14. e bt sh at
5. sin at		15. e bt ch at
6. cos at		16.e±bt(ch at± sh at)
7. e bt sin at		17. f(t)	F(p)
8. e bt cos at		18. f(t)	pF(p)-f(0)
9.		19. f(t)	p2F(p)-pf(0)-f(0)
10.		20. f(k)(t)	pkF(p)-[pk-1f(0)+ +pk-2f'(0)+...+f(k-1)(0)]

^*) в таблице 4.1 а >0, b > 0

^**) в строках 2, 4, 5, 7, 12, 14 таблицы 4.1 n! и число а > 0 в изображении F(p) можно переносить в соответствующий оригинал f(t) следующим образом:

sin at или ; константа с > 0 выносится за

знак преобразования: c  sin at

 Определение 4.4: Уравнение (4.4) называется операторным уравнением.

2) из (4.4) получим изображение Х(p):

. (4.5)

3) по таблице 4.1 изображений найдем оригинал x(t), который соответствует изображению X(p) и является решением данного уравнения (4.2).

 Пример 4.1. Найти решение дифференциального уравнения x+2x+x=te^-t :

а) общeе; б) частное, при начальных условиях x₀=x(0)=1; x₀=x(0)=2.

Pешение.

1. Обозначим изображение искомой функции x(t) через Х(p): x(t) X(p).

2. Используя строки 4, 18, 19, таблицы 4.1 оригиналов и изображений, находим изображения всех величин, входящих в данное уравнение:

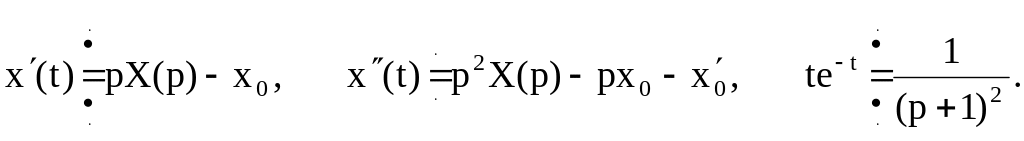
3. Подставляя найденные изображения в данное уравнение, получим операторное уравнение:

(p²+2p+1) X(p)–(p+2)x₀-x₀= .

4. Отсюда определяем:

.

5. По таблице 4.1 оригиналов и изображений, строка 3 соответственно при а=+1, n=1; а=+1, n=2; а=+1, n=4; находим оригинал x(t), соответствующий полученному изображению X(p). Предварительно X(p) преобразуем к виду^*):

Тогда получаем общее решение:

Положим x₀ = C₁ , x₀ + x₀ =C₂ . В результате:

6. При заданных начальных условиях находим частное решение:

x(t)=

 Ответ: a)

б)

При решении системы линейных дифференциальных уравнений с постоянными коэффициентами операционным методом вместо одного операторного уравнения получим систему операторных уравнений, представляющих собой линейные алгебраические уравнения относительно неизвестных изображений искомых функций.

^) Для разложения x(p) на простейшие дроби можно использовать систему Mathcad 6.0⁺ или Maple VR4.

 Пример 4.2. Найти решение системы дифференциальных уравнений

при начальных условиях x₀=x(0), y₀=y(0).

Решение.

1. Обозначим .

2. Найдем по таблице 4.1, п.3, 18 изображения

x'(t) pX(p)–x₀, y'(t) pY(p)–y₀,

3. Получим операторную систему

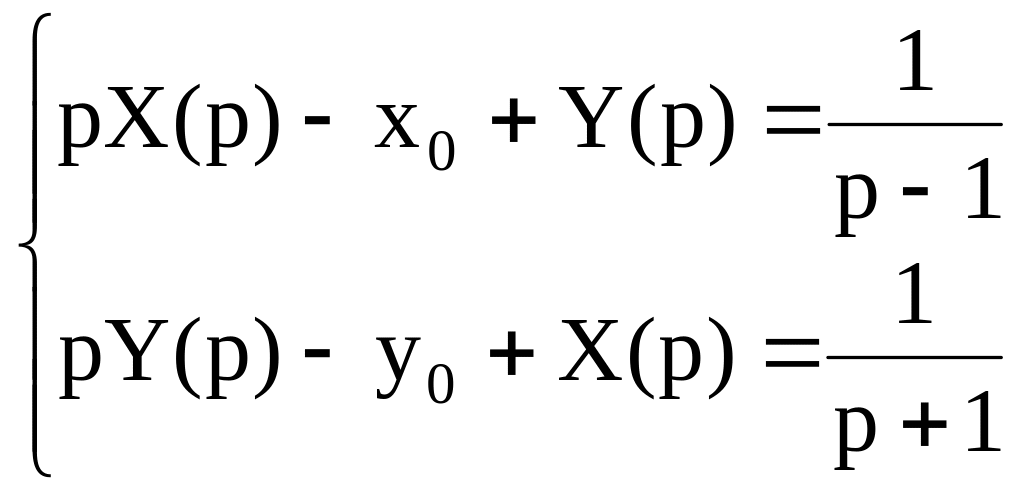
3. Отсюда определяем:

3. По таблице 4.1 оригиналов и изображений находим искомые функции x(t) и y(t):

• Ответ:

Пусть требуется найти решение (x(t), y(t)) системы ^) дифференциальных уравнений

(4.6)

удостоверяющее начальным условиям x(0)=x₀ , y(0)=y₀.

) уравнение (4.2) n-го порядка можно привести к системе n дифференциальных уравнений 1-го порядка. Так, в уравнении из примера 4.1 полагая x=y, a₁₁=f₁(t)=0, a₁₂=1, a₂₁=-1, a₂₂=-2, f₂ (t) = t e^-t, получим систему

Перейдем от оригиналов к изображениям (см. п. 17, 18 таблицы 4.1)

x(t) X(p), y(t) Y(p), f₁(t) F₁(p), f₂(t) F₂(p), (4.7)

x(t) pX(p)–x₀, y(t) pX(p)–y_0. (4.8)

Изображение системы (4.6) запишется следующим образом:

(4.9)

или (4.9)΄

Система операторных уравнений (4.9)΄ есть система линейных алгебраических уравнений относительно X(p) и Y(p). Её решение можно найти любым известным методом. Решим систему (4.9)΄ по формулам Крамера. Находим определитель d системы (4.9)΄ и определители d1 и d2 искомых величин X(p) и Y(p):

(4.10)

Откуда

X(p) = , Y(p) = . (4.11)

Затем производим разложение X(p) и Y(p) на элементарные дроби и находим оригиналы x(t) и y(t).

 Пример 4.3. Найти решение системы обыкновенных дифференциальных уравнений

(4.12)

удовлетворяющее начальным условиям x(0) = 1, y(0) =2 операционным методом.

Решение в системе MathCAD 6.0⁺ (см.§6.1.1). По условию задачи имеем (см.(4.6)): а₁₁=3, а₁₂=5, f₁(t)=e^4t·cos5t, a₂₁=7, a₂₂=2, f₂(t)=e^‑3t·cos2t, t₀ =0, x₀=1, y₀=2. Найдем решение (x(t),y(t)) заданной системы.

По таблице 4.1 (строки 17 и 18) находим изображения исходных функций x(t), y(t) и их производных x'(t), y'(t), учитывая, что Mathcad вместо переменной p использует использует переменную s. Имеем для заданных начальных условий

x(t) X(s), x'(t) s∙X(s)‑x(0)=s∙X(s)–1;

y(t) Y(s), y'(t) s∙Y(s)‑y(0)=s∙Y(s)-2;

Теперь с помощью команды Преобразование Лапласа (см. пример 6.1.10) находим изображения функций f₁(t) и f₂(t):

{e^–4*t*cos(5*t)}

В меню МатематикаАвтоматический режимИспользовать символику щелкаем мышью () на переменной преобразования t и выбираем из меню СимволикаПреобразованияПреобразование Лапласа.

Получаем (см. рис. 4.1), включив комментарии (§ 6.1.6), соответствующее изображение. Аналогично,

{e ^–3*t*cos(2*t)}

() на t и выбираем из меню Символика Преобразования Преобразование Лапласа.

Теперь, используя символьный знак равенства [Ctrl]=, записываем систему операторных уравнений вида (4.9) и решаем ее с помощью функции Find (см. § 6.1.6, пример 6.1.14), определив вектор-столбец искомых функции .

Вводим

{Given}

{s*X–1Ctrl=3*X+5*Y+копируем изображение F1(s)} (см. § 6.1.1, п. Ввод и редактирование выражений)

{s*Y–2Ctrl=7*X+2*Y+копируем изображение F2(s)}

{Find(X,Y)Ctrl.}

{X(s)=}, {Y(s)=}

Чтобы получить оригиналы для x(t) и y(t), щелкаем мышью на переменной преобразования s из меню Символика, выбираем последовательно ПреобразованияОбратное преобразование Лапласа. Тоже делаем для y(t).

Проверка. Найденные выражения обозначим через x(t) и y(t).

{x(t): копируем соответствующий оригинал x(t) }

{y(t): копируем оригинал y(t)}

Производные от x(t) и y(t) определяем как

{x(t): копируем (cм. § 6.1.1) оригинал x(t) t Shift F9}

{y(t): копируем оригинал y(t) t Shift F9}

Выражения x(t), y(t), x(t), y(t) подставляем в уравнения преобразованной системы (4.12) и упрощаем:

{x(t)–3*x(t)–5*y(t) окружаем рамкой Символика Упростить}

{y(t)–7*x(t)–2*y(t) окружаем рамкой Символика Упростить}.

Поскольку в результате упрощения полученны функции и , то решение x(t), y(t) системы (4.12) найдено верно.

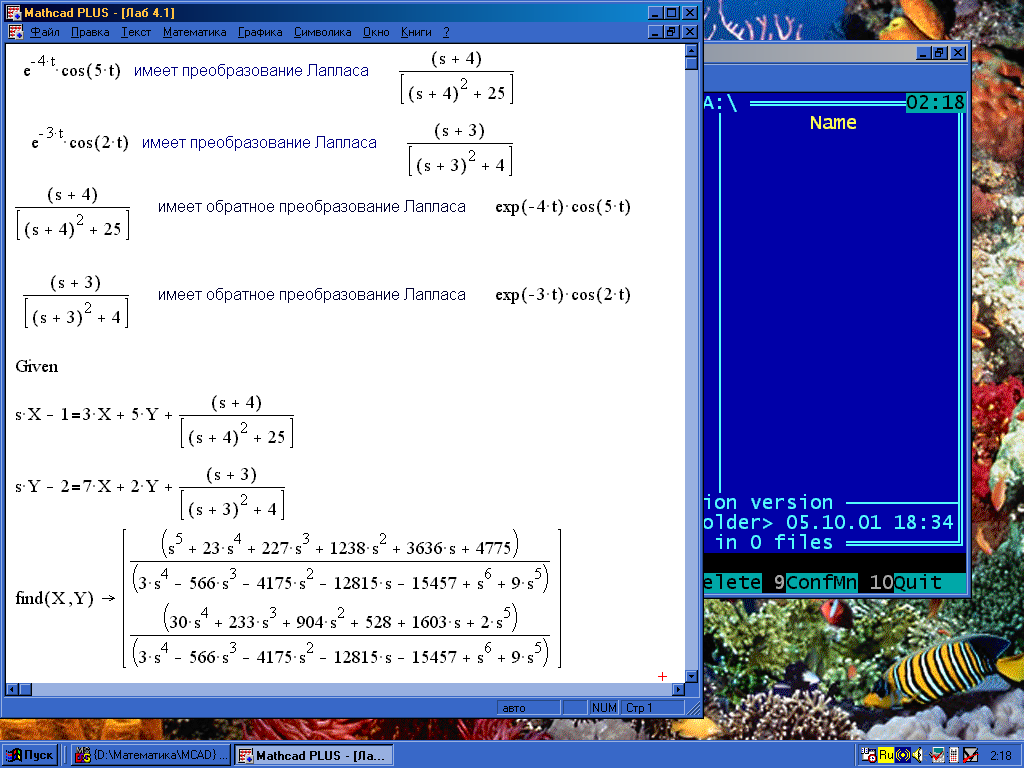
Рис. 4.1.

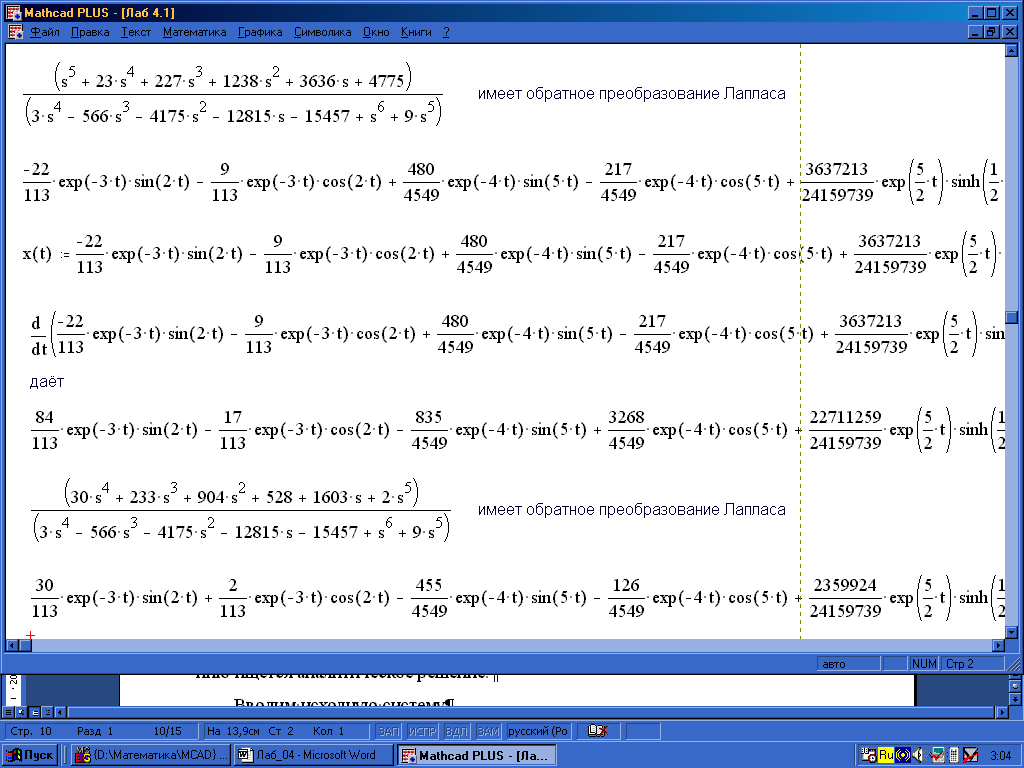
Рис. 4.2.

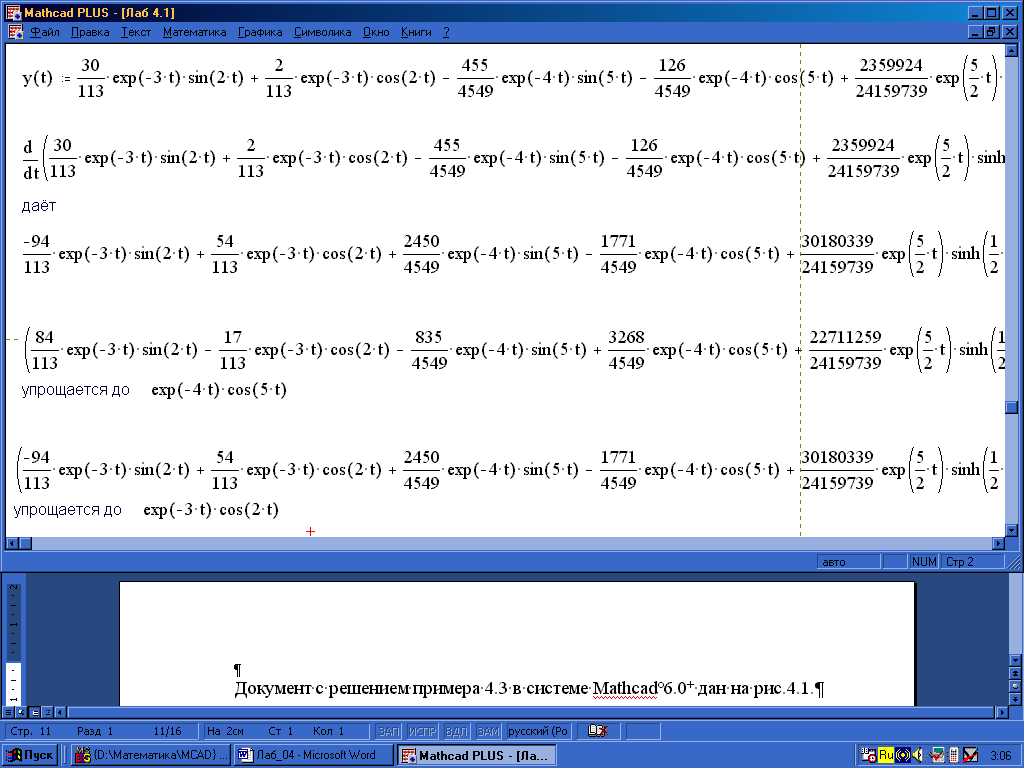
Рис. 4.3.

Документ с решением примера 4.3 в системе Mathcad 6.0⁺ дан на рис.4.1-4.3.

Решение в системе Maple VR4. Загружаем Maple VR4 (см.6.2.1) и используем команду dsolve с опцией method=laplace (см. пример 6.2.13). Вводим исходную систему sys. Искомое решение (x(t), y(t)) обозначаем как fcns. Для решения заданной системы операционным методом функции dsolve указываем: решаемую систему sys с начальными условиями x(0)=1,y(0)=2; искомые функции fcns и метод решения laplace. Результат решения представлен на рис. 4.2.–4.7.

Если метод решения не указывать, получим то же самое, так как по умолчанию ищется аналитическое решение.

Вводим исходную систему

>sys:= diff(x(t),t)=3*x(t)+5*y(t)+e^(-4*t)*cos(5*t),

diff(y(t),t)=7*x(t)+2*y(t)+e^(-3*t)*cos(2*t);

fcns:={x(t),y(t)}: dsolve({sys,x(0)=1,y(0)=2},fcns,laplace);

На экране видим:

>sys:= x(t)=3x(t)+5y(t)+ ,

y(t)=7x(t)+2y(t)+

x(t)=…

Далее задаем: >dsolve({sys,x(0)=1,y(0))=2,fcns};

Получаем: x(t)=…

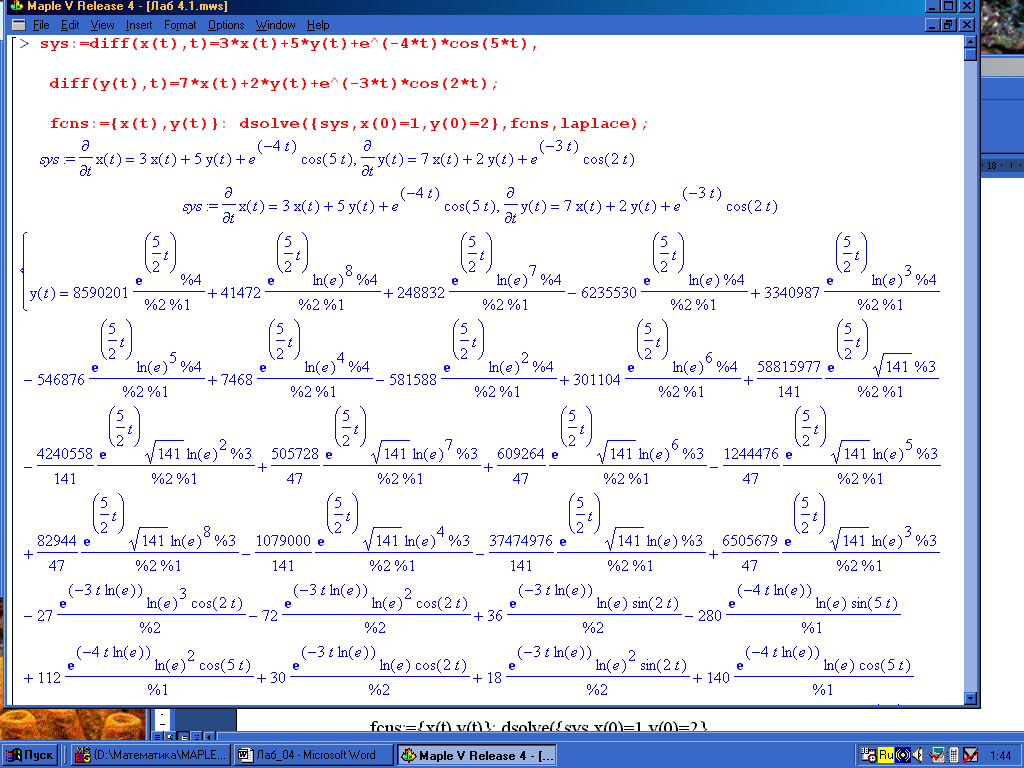
Рис. 4.4.

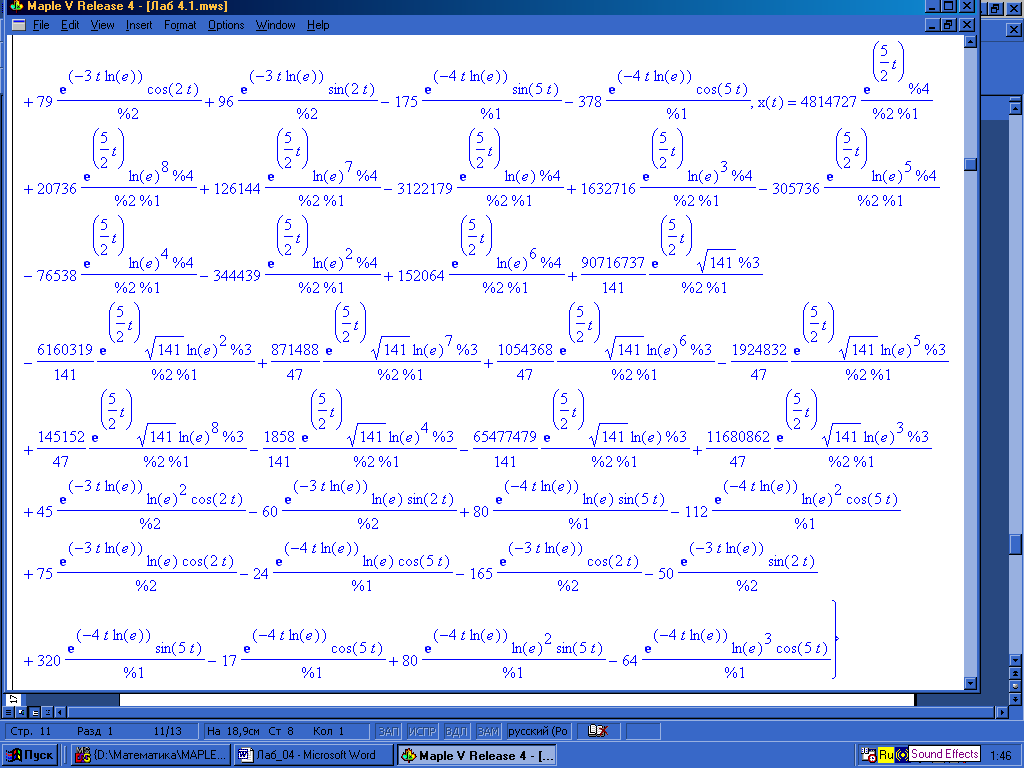
Рис. 4.5.

Рис. 4.6.

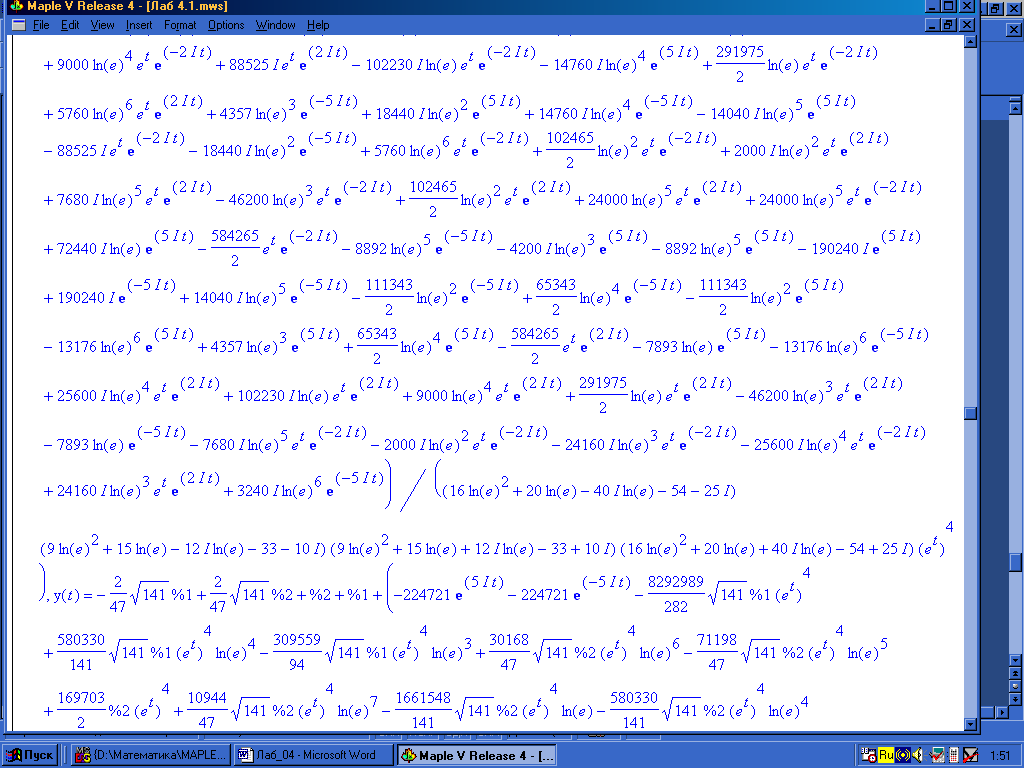
Рис. 4.7.

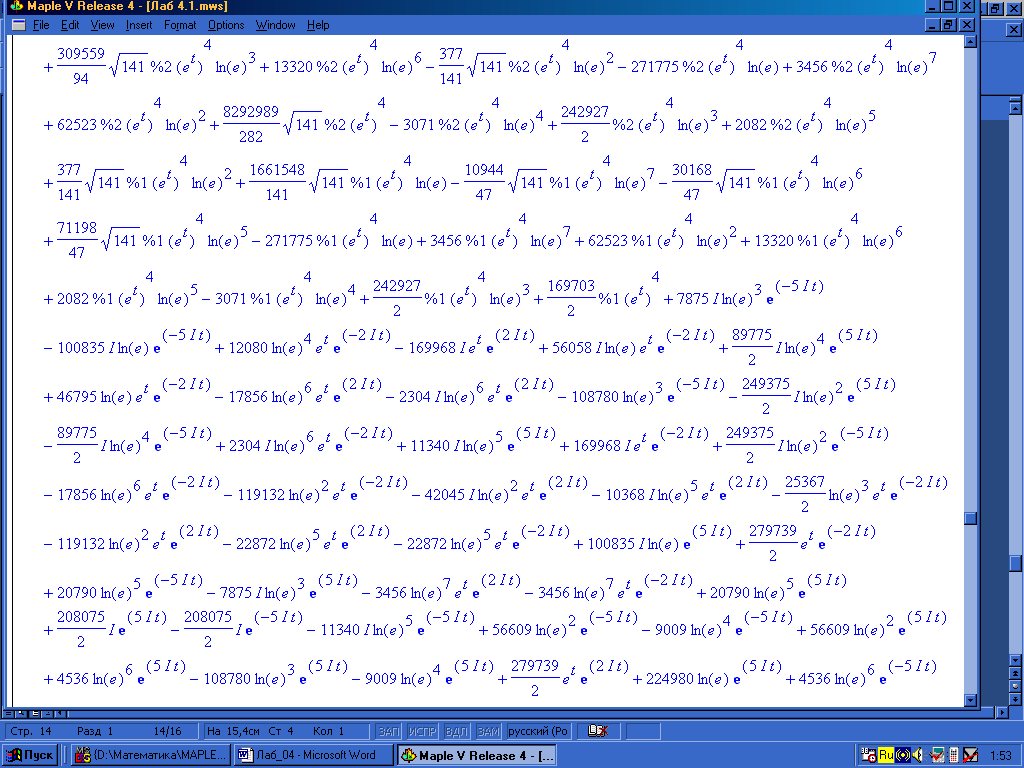
Рис. 4.8.

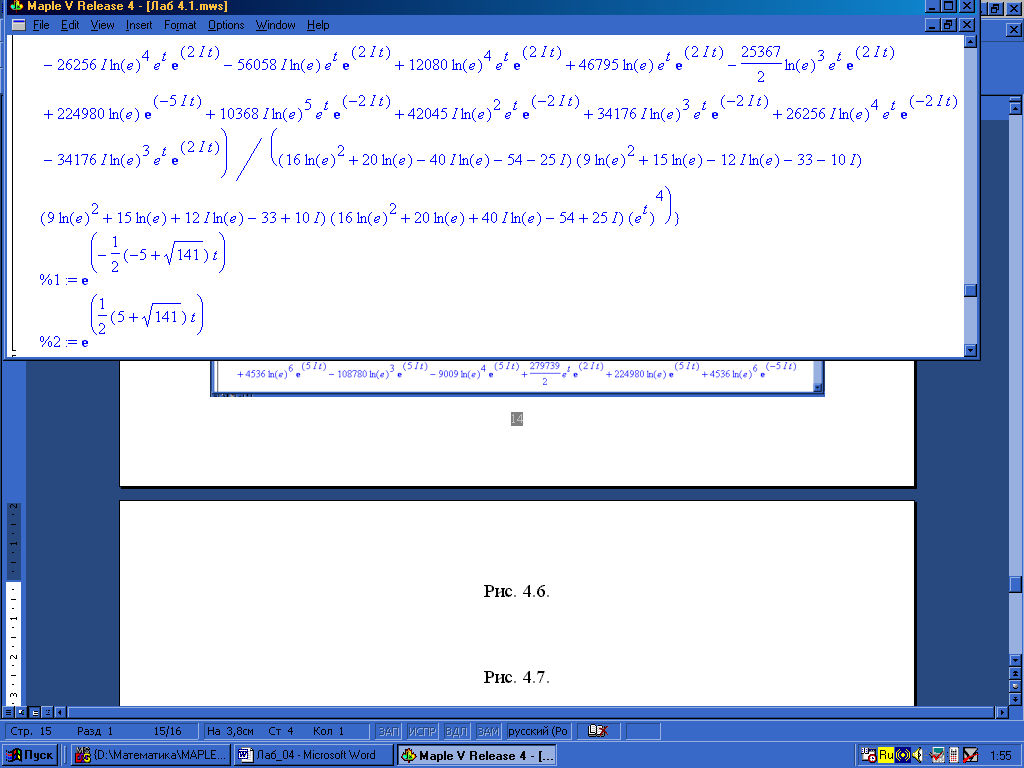
Рис. 4.9.

Контрольные вопросы

1. Преобразование Лапласа.

2. Требования к оригиналу.

3. Таблица оригиналов и изображений.

4. Операторное уравнение.

5. Решение линейного дифференциального уравнения n-го порядка с постоянными коэффициентами.

6. Решение системы дифференциальных уравнений операционным методом.

7. Решение дифференциальных уравнений и систем в интегрированных пакетах MathCad 6.0⁺ и Maple V.

Задания к лабораторной работе № 4

Найти решение системы дифференциальных уравнений, удовлетворяющее заданным начальным условиям. Сделать проверку.

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

Порядок выполнения работы

1. Получить допуск к работе.

2. Построить математическую модель задачи.

3. Подготовить данные для ввода в ПЭВМ.

4. Получить решение задачи.

5. Cделать проверку.

6. Составить отчет.

Содержание отчета

1. Текст задачи.

2. Формулировка математической модели.

3. Данные ввода в ПЭВМ.

4. Результаты расчетов на ПЭВМ.

5. Интерпретация полученного решения.

Лабораторная работа № 5

Построение статистической модели нормальной случайной величины. Подбор эмпирических формул

Литература: [3, гл.15, § 1-4; 5, гл. 17, § 1-4; 6, гл.2, § 17; 7, гл. 2, § 1-12; 11, пример 13]

I. Построение статистической модели нормальной случайной величины

Постановка и решение задачи

Формулировка задачи.

Построить статистическую модель нормальной случайной величины Х с математическим ожиданием М(X) и средним квадратическим отклонением (X) при выборке объемом n=100.

 Определение 5.1. Под статистической моделью нормальной случайной величины Х с параметрами М(X) и (X) понимаем эмпирический закон распределения плотности относительных частот нормальной случайной величины Х (гистограмму) с выборочным средним х_в и выборочным средним квадратическим отклонением _в.

Статистическая модель строится на основе функции Лапласа (рис. 5.1.а))

Ф(х)=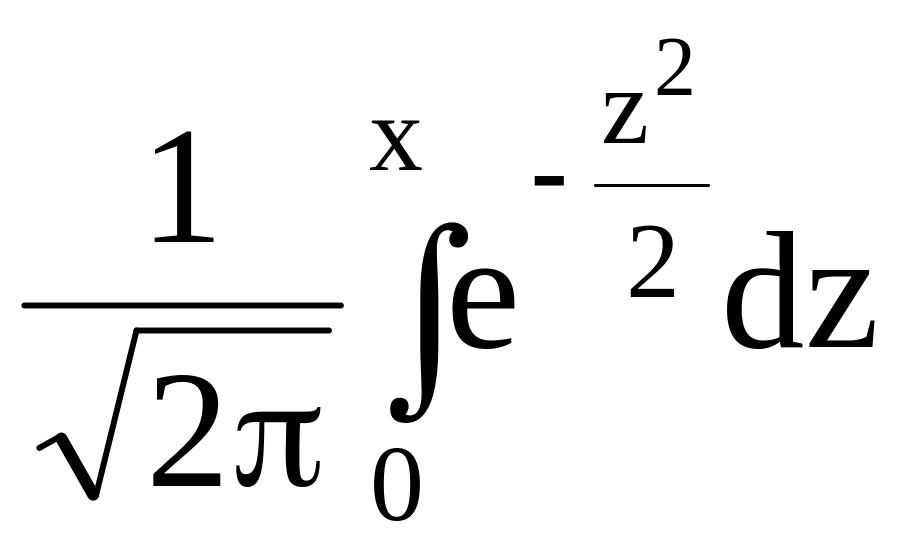

С помощью таблицы 5.1. значений Ф(х) представляется возможность определить вероятность попадания случайной нормированной нормальной величины Х₀, М(Х₀)=0, (Х₀)=1 в интервал (0;x):

P(0<X<x) = Ф(х).

Рис. 5.1.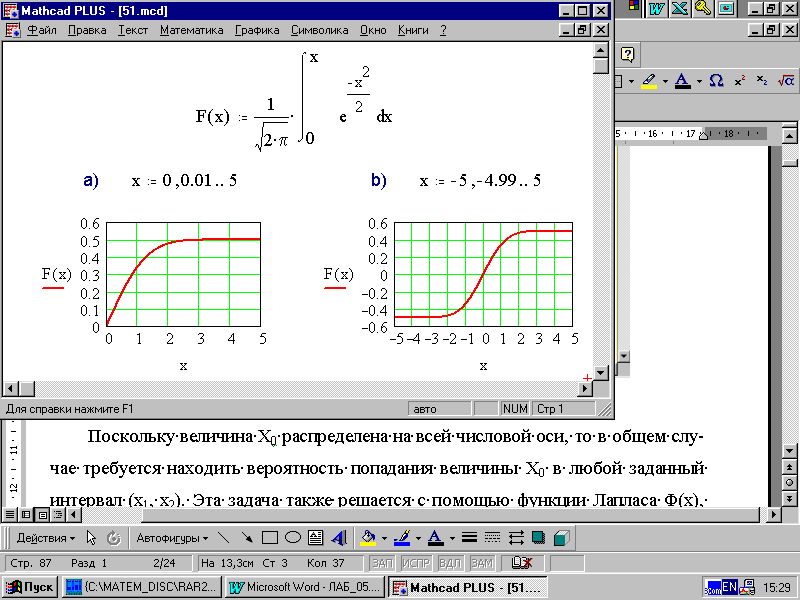

Поскольку величина Х₀ распределена на всей числовой оси, то в общем случае требуется находить вероятность попадания величины Х₀ в любой заданный интервал (х₁, х₂). Эта задача также решается с помощью функции Лапласа Ф(х), если учесть ее свойство нечетности Ф(–х) = –Ф(х).

График Ф(х) для х(–;+) представлен на рис. 5.1 b).

Ф(–х) = – Ф(х)

По определению функции распределения F(x) величины Х₀:

F(x)=P(X₀x)=P(–<X₀<x)= =0,5+Ф(х).

Тогда Р(х₁<X₀<x₂)=F(x₂)–F(x₁)=Ф(х₂)–Ф(х₁).

Графики Ф(х) и F(x) даны на рис. 5.2.

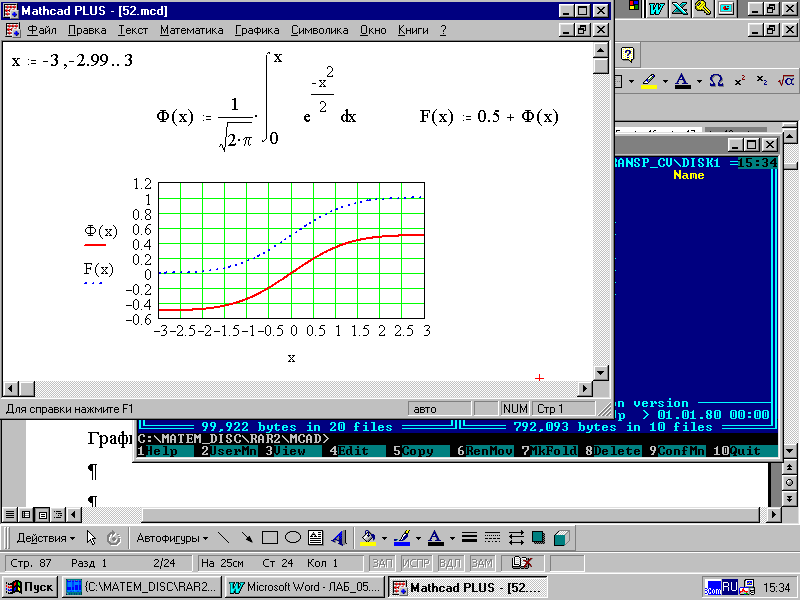
Рис. 5.2.

Для построения статистической модели нормальной случайной величины Х необходимо с равной вероятностью выбрать 100 значений x_i, i = из нормального распределения случайной величины Х при заданных М(Х) и (Х) и произвести статистическую обработку полученной выборки. Каждое значение х_i, i = при этом определим по формуле:

x_0i=  x_i=x_0i(X)+M(X),

где х_0i – нормированное значение выборочного значения х_i.

В свою очередь, х_0i, i = находим, используя табл. 5.2 равномерного распределенных в интервале (0,1) случайных чисел r_i и табл. 5.1 значений функции Лапласа Ф(х) по нижеприведенному правилу. Если расчеты проводятся на основе системы MathCAD, то обращение к этим таблицам заменяются соответствующими вычислениями на ПЭВМ.

 Определение 5.2. Под случайными числами r_i понимаем возможные отдельные значения непрерывной случайной величины R, равномерно распределенной в интервале (0,1).

Правило нахождения значений х_0i , i = проиллюстрировано на рис. 5.3.

1) если случайное число r>0,5, то r_i =Ф(х_0i)+0,5=F(x_0i)Ф(х_0i)=r_i –0,5x_0i,

2) если r<0,5, то r_i =–Ф(x_0i)+0,5=F(–x_0i)–Ф(x_0i)=r_i –0,5Ф(–x_0i)=r_i–0,5–x_0i.

Таким образом, число x_0i ищем по таблице значений Ф(х), как соответствующее значению Ф(х_0i)=r_i–0,5. При этом, чтобы получить отрицательное значение, т.е. –х_0i, при r_i<0,5, необходимо значение x_0i, соответствующее Ф(x_0i) = r_i‑0,5, взять со знаком минус.

 Пример 5.1. Построить статистическую модель нормальной случайной величины Х с математическим ожиданием М(Х)=2 и средним квадратичным отклонением (Х)=3 при выборке объемом n=100, начиная с числа .

Решение. 1. Из табл. 5.2 последовательно слева направо, начиная с числа , выписываем 100 случайных чисел r_i, i= , равномерно распределенных в интервале (0;1), и получим: 0,25; 0,33; 0,76; 0,52; 0,01;...; 0,77; 0,66; 0,06; 0,57.

2. По вышеприведенному правилу, используя табл. 5.1 значений функции Лапласа Ф(х), получим выборку объемом n=100 нормированной нормальной случайной величины Х₀ : x_0i, i= .

Например: r₁=0,25(<0,5)=–Ф(х₀₁)+0,5=F(–x₀₁)–Ф(х₀₁)=–0,25

[Ф(‑х₀₁)=–0,25; Ф(х₀₁)=–0,25, х₀₁ ищем по табл. 7.1 значений Ф(х), как соответствующее значению Ф(х₀₁)=0,25 и придаем ему знак минус x₀₁ =–0,67 (соответствует значению функции Ф(х)=0,24860,25);

r₂=0,33(<0,5)=–Ф(х₀₂)+0,5=F(–x₀₂)–Ф(х₀₂)=-0,17х₀₂=–0,44;

r₃=0,76(>0,5)=Ф(х₀₃)+0,5=F(x₀₃)Ф(х₀₃)=0,26х₀₃=0,71;

...................................................................................................

r₁₀₀=0,57(>0,5)=Ф(х₁₀₀)+0,5=F(x₁₀₀)Ф(х₁₀₀)=0,07х₁₀₀=0,18

(соответствует значению функции Ф(х)=0,07140,07).

3. По формуле x_i=x_0i(X)+M(X), i= получим выборку объемом n=100 заданной нормальной случайной величины Х.

4. Определим точечные оценки х_в и _в соответственно параметров М(Х) и (Х) закона распределения вероятностей заданной нормальной случайной величины Х:

x_в= , _в= .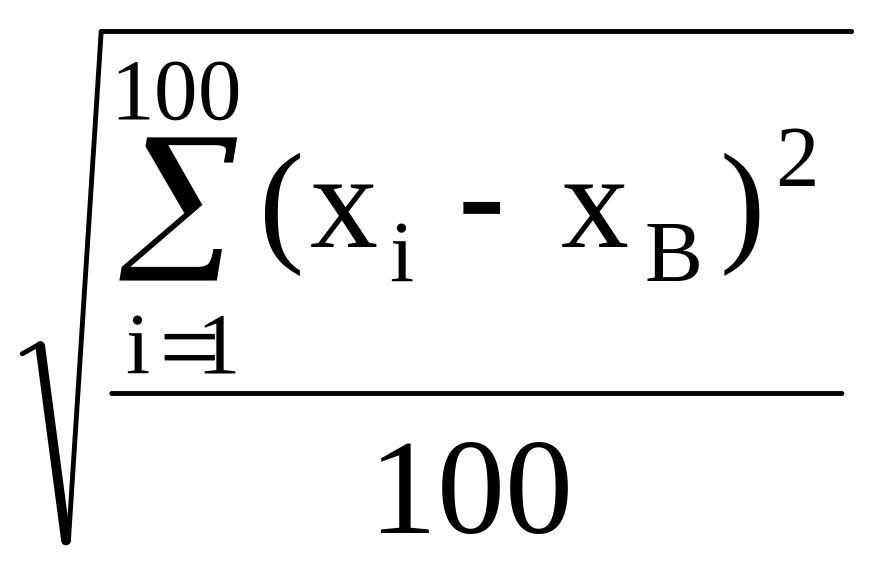

5. Строим график эмпирической плотности относительных частот случайной величины Х (гистограмму):

а) из всех значений x_i , i = выбираем наименьшее x_min, обозначаем его через х₁, и все остальные значения располагаем в порядке возрастания: x_min=x₁<x₂<x₃< ... <x₁₀₀

б) полученный ряд чисел для простоты разобьем на 10 равных интервалов. Длина каждого интервала, очевидно, равна: .

в) в каждом из интервалов подсчитаем частоту n_i наблюдения чисел x_i и определим относительную частоту и плотность относительной частоты .

г) построим график (гистограмму) эмпирической плотности относительных частот случайной величины Х. Примерный вид графика (ступенчатая линия) представлен на рис. 5.3.

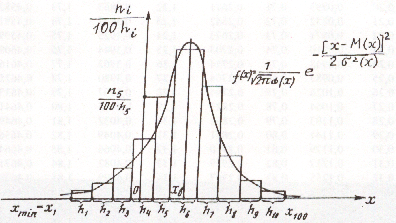
Рис. 5.3

Таблица 5.1

Таблица значений функции Лапласа Ф(х)=

х	Ф(х)	х	Ф(х)	х	Ф(х)	х	Ф(х)
1	2	3	4	5	6	7	8
0,00	0,0000	0,01	0,0040	0,02	0,0080	0,03	0,0120
0,04	0,0160	0,55	0,2088	1,06	0,3554	1,57	0,4418
0,05	0,0199	0,56	0,2123	1,07	0,3577	1,58	0,4429
0,06	0,0239	0,57	0,2157	1,08	0,3599	1,59	0,4441
0,07	0,0279	0,58	0,2190	1,09	0,3621	1,60	0,4452
0,08	0,0319	0,59	0,2224	1,10	0,3643	1,61	0,4463
0,09	0,0359	0,60	0,2257	1,11	0,3665	1,62	0,4474
0,10	0,0398	0,61	0,2291	1,12	0,3686	1,63	0,4484
0,11	0,0438	0,62	0,2324	1,13	0,3708	1,64	0,4495
0,12	0,0478	0,63	0,2357	1,14	0,3729	1,65	0,4505
0,13	0,0517	0,64	0,2389	1,15	0,3749	1,66	0,4515
0,14	0,0557	0,65	0,2422	1,16	0,3770	1,67	0,4525
0,15	0,0596	0,66	0,2454	1,17	0,3790	1,68	0,4535
0,16	0,0636	0,67	0,2484	1,18	0,3810	1,69	0,4545
0,17	0,0675	0,68	0,2517	1,19	0,3830	1,70	0,4554
0,18	0,0714	0,69	0,2549	1,20	0,3849	1,71	0,4564
0,19	0,0753	0,70	0,2580	1,21	0,3869	1,72	0,4573
0,20	0,0793	0,71	0,2611	1,22	0,3863	1,73	0,4582
0,21	0,0832	0,72	0,2642	1,23	0,3907	1,74	0,4591
0,22	0,0871	0,73	0,2673	1,24	0,3925	1,75	0,4599
0,23	0,0910	0,74	0,2703	1,25	0,3944	1,76	0,4608
0,24	0,0948	0,75	0,2734	1,26	0,3962	1,77	0,4616
0,25	0,0987	0,76	0,2764	1,27	0,3980	1,78	0,4625
0,26	0,1026	0,77	0,2794	1,28	0,3997	1,79	0,4633
0,27	0,1064	0,78	0,2823	1,29	0,4015	1,80	0,4641
0,28	0,1103	0,79	0,2852	1,30	0,4032	1,81	0,4649
0,29	0,1141	0,80	0,2881	1,31	0,4049	1,82	0,4656
0,30	0,1179	0,81	0,2910	1,32	0,4066	1,83	0,4664
0,31	0,1217	0,82	0,2939	1,33	0,4082	1,84	0,4671
0,32	0,1255	0,83	0,2967	1,34	0,4099	1,85	0,4678
0,33	0,1293	0,84	0,2995	1,35	0,4115	1,86	0,4686
0,34	0,1331	0,85	0,3023	1,36	0,4131	1,87	0,4693
0,35	0,1368	0,86	0,3051	1,37	0,4147	1,88	0,4699

Продолжение табл. 5.1

1	2	3	4	5	6	7	8
0,36	0,1406	0,87	0,3078	1,38	0,4262	1,89	0,4706
0,37	0,1443	0,88	0,3106	1,39	0,4177	1,90	0,4313
0,38	0,1480	0,89	0,3133	1,40	0,4192	1,91	0,4719
0,39	0,1517	0,90	0,3159	1,41	0,4207	1,92	0,4726
0,40	0,1554	0,91	0,3186	1,42	0,4222	1,93	0,4732
0,41	0,1591	0,92	0,3212	1,43	0,4236	1,94	0,4738
0,42	0,1628	0,93	0,3238	1,44	0,4251	1,95	0,4744
0,43	0,1664	0,94	0,3264	1,45	0,4265	1,96	0,4750
0,44	0,1700	0,95	0,3289	1,46	0,4279	1,97	0,4756
0,45	0,1736	0,96	0,3315	1,47	0,4292	1,98	0,4761
0,46	0,1772	0,97	0,3340	1,48	0,4306	1,99	0,4767
0,47	0,1808	0,98	0,3365	1,49	0,4319	2,00	0,4772
0,48	0,1844	0,99	0,3389	1,50	0,4332	2,02	0,4783
0,49	0,1879	1,00	0,3413	1,51	0,4345	2,04	0,4793
0,50	0,1915	1,01	0,3438	1,52	0,4357	2,06	0,4803
0,51	0,1950	1,02	0,3461	1,53	0,4370	2,08	0,4812
0,52	0,1985	1,03	0,3485	1,54	0,4382	2,10	0,4821
0,53	0,2019	1,04	0,3508	1,55	0,4394	2,12	0,4830
0,54	0,2054	1,05	0,3531	1,56	0,4406	2,14	0,4838
2,16	0,4846	2,44	0,4927	2,72	0,4967	3,00	0,49865
2,18	0,4854	2,46	0,4931	2,74	0,4969	3,20	0,49931
2,20	0,4861	2,48	0,4934	2,76	0,4971	3,40	0,49966
2,22	0,4868	2,50	0,4938	2,78	0,4973	3,60	0,499875
2,24	0,4875	2,52	0,4941	2,80	0,4974	3,80	0,499928
2,26	0,4881	2,54	0,4945	2,82	0,4976	4,00	0,499968
2,28	0,4887	2,56	0,4948	2,84	0,4977	4,50	0,499997
2,30	0,4893	2,58	0,4951	2,86	0,4979	5,00	0,499997
2,32	0,4898	2,60	0,4953	2,88	0,4980
2,34	0,4904	2,62	0,4956	2,90	0,4981
2,36	0,4909	2,64	0,4959	2,92	0,4982
2,38	0,4913	2,66	0,4961	2,94	0,4984
2,40	0,4918	2,68	0,4963	2,96	0,4985
2,42	0,4922	2,70	0,4965	2,98	0,4986

Таблица 5.2

Таблица равномерно распределенных в интервале (0;1) случайных чисел.