Организация вычислений на пэвм с помощью

пакета программ MathCAD 6.0⁺

Покажем, как получить реализации Х_i равномерно распределенных в интервале (0;1) случайных чисел и построить статистическую модель нормальной случайной величины Z с помощью системы MathCAD 6.0⁺.

 Пример 5.2. Пусть Z-случайная величина, распределенная по нормальному закону с параметрами: M(Z)=2, (Z)=3, где М – математическое ожидание,  – среднее квадратичное отклонение.

Требуется промоделировать n=200 значений этой случайной величины. Найти оценки для математического ожидания, дисперсии и среднего квадратического отклонения, построить гистограммы частот и относительных частот.

Решение. Будем исходить из следующих соображений:

Пусть Х – случайная величина, равномерно распределенная в промежутке (0,1). На основании центральной предельной теоремы А.М. Ляпунова случайная величина Y со значениями

y_j= (5.1)

приближенно является нормированной нормальной с параметрами M(Y)=0, (Y)=1 (M(X)=0.5 – математическое ожидание равномерно распределенной случайной величины Х).

Поэтому для получения одного значения y_j нормальной случайной величины Y необходимо взять не менее 12^*) значений (m12) x_i равномерно распределенной в промежутке (0;1) случайной величины Х, т.е. взять не менее 12 различных реализаций Х₁, Х₂, ... , Х_m, m12 случайной величины Х. Тогда случайная величина Z=M(Z) + (Z)Y будет практически нормальной с заданными параметрами М(Z) и (Z).

^*)В примере 5.1 для простоты взята одна реализация случайной величины R={r_i}, i= , равномерно распределенной в интервале (0;1). При увеличении m случайная величина Y достаточно быстро сходится к нормальному распределению.

Загружаем систему MathCAD 6.0⁺ (см. 6.1.1.) и выполняем следующие операции:

1. Строим матрицу А, содержащую 12 строк, i=0,1,…,11, и 200 столбцов, j=0,1,…, 199, элементами А_ij которой являются случайные числа х_i из промежутка (0;1). Генерирование равномерно распределенных случайных чисел из (0;1) осуществляется с помощью функции rnd(1).

Печатаем {i:0;11}, {j: 0;199}, {A[i,j:rnd(1)} (см. рис. 5.4.). Если ввести {А=}, MathCAD изобразит фрагмент матрицы А размерности 12200, в которой каждому элементу А_i,j будет присвоено произвольное число^**) из промежутка (0;1) с тремя знаками после запятой.

Таким образом, каждая строка матрицы А есть одна из реализаций X_i, содержащая 200 значений, равномерно распределенной на (0;1) случайной величины Х.

2. Вводим исходные данные для математического ожидания М(Z)=2, среднего квадратичного отклонения s=(Z)=3 и вводим формулу для определения значений Z_j искомой случайной величины Z.

Печатаем (см. §6.1.5) {M:2}, {s:3}, {Z[j:M+s*Ctrl4 (ACtrl6j –0.5)}.

Каждое значение Z_j случайной величины получается следующим образом. Из каждого элемента A^<j> (Ctrl6 – выделение j-того столбца матрицы А), j-того столбца, j=0,1,…,199, матрицы А вычитается число 0,5. Таким образом, все числа A_i,j, принадлежащие промежутку (0;1) попадают в промежуток . Затем новые элементы j-того столбца матрицы суммируются (Ctrl4). В результате получаются значения практически нормальной нормированной случайной величины с параметрами M=0 и =1, т.е. значения кривой Гаусса. Эти значения умножаются на =3 и складываются с M=2. Тогда Z_j , j=0,1,…,199, есть значения практически нормальной случайной величины Z, которую необходимо построить.

^**) Поскольку функция rnd есть генератор случайных чисел, то при каждом ее запуске значения A_ij будут меняться.

Для иллюстрации выведем на экран фрагмент матрицы А; 0, 50, 150-ый столбцы матрицы А, фрагмент случайной величины Z {А=}, {ACtrl60=}, {ACtrl650=}, {ACtrl6150=},{Z=} (см. рис. 5.4–5.5).

Чтобы увидеть невидимые элементы матрицы А, выделите ее, щелкнув по ней () и, используя горизонтальную и вертикальную линии прокрутки, просмотрите интересующие области.

Сделаем также графическую интерпретацию значений элементов A_ij матрицы А. На нижеследующем рисунке на оси абсцисс располагаются столбцы 0,1,…,199 матрицы А. По оси ординат точками из промежутка (0;1) изображаются числа, являющиеся элементами A_i,j матрицы (см. §6.1.4). Очевидно, что вся плоскость графика заполнена точками равномерно, т.е. нет такого, чтобы точки, соответствующие числу 0,5, наблюдались чаще, а числу 0,1 или 1,0 – реже.

Рис. 5.4.

3. Находим оценки для математического ожидания, дисперсии и среднего квадратического отклонения полученных n=200 значений рассматриваемой случайной величины Z двумя способами. Вначале согласно определению каждой из указанных характеристик, а затем посредством функций вычисления статистических оценок случайных совокупностей, реализованных в MathCAD 6.0⁺: mean(Z), var(Z), stdev(Z).

{M1Ctrl4Z/200}, {M1=}, {mean(Z)=},

{Z1[j:(Z[j–M1)^2},

{D1Ctrl4(Z1/200}, {D1=}, {var(Z)=},

{s1\D1}, {s1=}, {stdev(Z)=}.

Очевидно, что M1 и s1 практически совпадают с заданными M=2 и =3.

4. Подготовим данные для построения требуемых гистограмм.

Определим число k интервалов, на которые нужно разделить полученную серию значений рассматриваемой случайной величины {k:1+3.22*log(200) }, {k=}.

Округляем до ближайшего целого {k:9}.

Находим величину шага h для построения гистограммы {h:max(Z)–min(Z)/k},{min(Z)=}, {max(Z)=}, {h=}

Находим границы r_n девяти интервалов, на которые разбит промежуток, которому принадлежат Z_j от min(Z) до max(Z). Печатаем {n:0;k}, {r[n:min(Z)+h*n}.

Посредством функции hist определяем число N_m значений Z_j величины Z, попавших в каждый из найденных интервалов r_n. Вводим {m:0; k–1}, {N:hist(r,Z)}, {r[1–r[0=}, {r[6–r[5=}, {r[9–r[8=}, {N[0=}, {N[4=}, {N[8=}, {r[n=}, {N=}.

В результате получаем 9 интервалов одинаковой длины h=1,75, в каждый из которых в порядке возрастания индексов граничных точек попало соответственно N₀=5, N₁=13 , …, N₈=7 значений Z_j случайной величины Z. Иными словами функция hist возвращает вектор N, в котором N_i есть число значений из Z, удовлетворяющих условию:

, n=0,1,…,9; m=0, 1,…,8.

Таким образом, получено статистическое распределение случайной величины Z – соответствие между интервалами r_n, в которые заключены наблюдаемые значения Z_j величины Z, и частотами N_i.

В гистограмме частот прямоугольники должны иметь одинаковую ширину h, а высоты должны быть равны отношению (плотность частоты). Тогда площадь i-го прямоугольника равна – сумме частот i-го интервала, а площадь гистограммы частот равна сумме всех частот N_i, т.е. объему выборки n=200.

Печатаем {N1[m:N[m/h}, {h*N1=}, {N1=} и строим гистограмму частот, где по оси абсцисс указываем r_m, а по оси ординат N1_m.

Рис. 5.5

Гистограмма относительных частот отличается от гистограммы частот тем, что по оси ординат откладывают плотности относительных частот W_i/h=N_i/( )=N1_i/n=N1_i/200. Соответственно площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.

Вводим {W1[m:N1[m/200}, {h*W1 Ctrl6m=}, {W1=}. Для построения гистограммы относительных частот разметка координатных осей следующая: ось абсцисс – r_m, ось ординат – W1_m.

Для проверки построим график (см. §6.1.4) функции плотности распределения вероятностей нормальной случайной величины с заданными параметрами M=2, =s=3:

f(x)= .

Печатаем {x:–10,-9.9;15}, {f(x):1/s*\2*CtrlP*exp(–(x–M)^2/2*s^2}

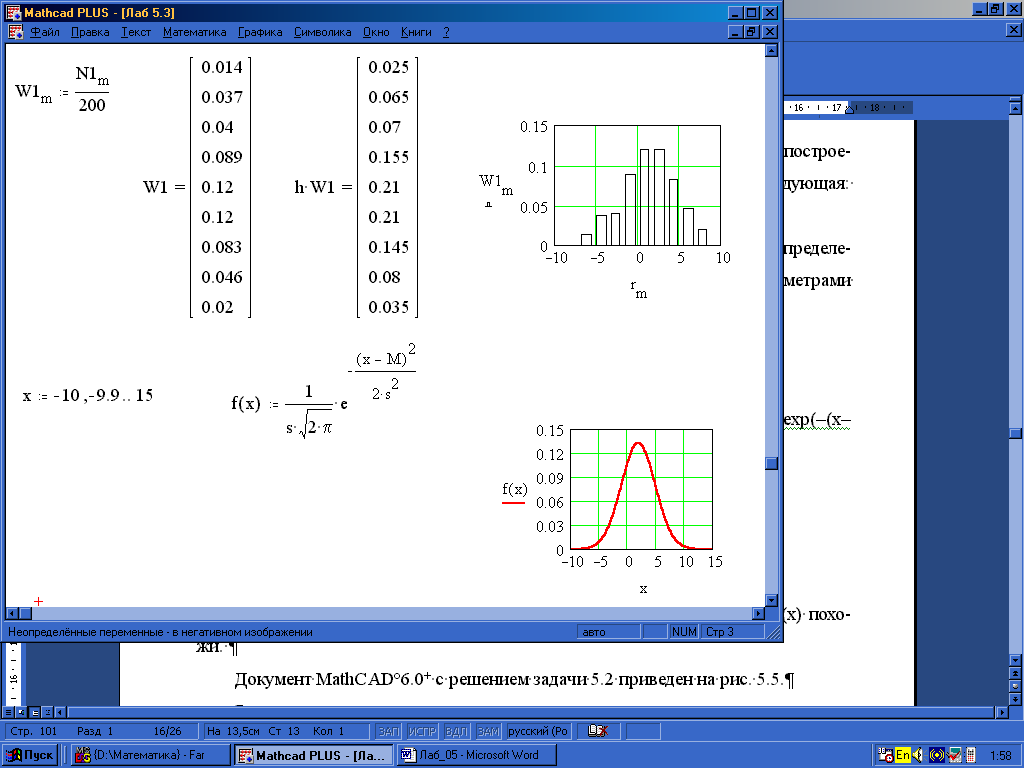
Рис. 5.6

Как видим гистограмма относительных частот и график функции f(x) похожи.

Документ MathCAD 6.0⁺ с решением задачи 5.2 приведен на рис. 5.4–5.6.