Задания к лабораторной работе № 2

1. Определить с точностью ^-6 все корни уравнения f(x)=0

2. Из железного листа с длиной l м и шириной s м отгибом полосок со всех четырех сторон сделать: а) ящик с объемом v₀ м³; б) ящик максимального объема. Найти соответствующие размеры ящиков.

1. I. x⁴+2.3x³-3.23x²–6.951x+1.4994=0; II. l =4.1, s =2.1, v₀=1.0.

2. I. x⁴+3.8x³-4.41x²–1.372x+2.8812=0; II. l =4.2, s =2.2, v₀=1.1.

3. I. x⁴+2.5x³-1.38x²–0.544x+0.448=0; II. l =4.3, s =2.3, v₀=1.2.

4. I. x⁴+2.4x³–0.38x²–0.984x+0.1881=0; II. l =4.4, s =2.4, v₀=1.3.

5. I. x⁴+2.3x³–0.77x²–3.087x+1.2348=0; II. l =4.5, s =2.5, v₀=1.4.

6. I. x⁴+2.3x³–0.4x²–0.404x+0.048=0 II. l =4.6, s =2.6, v₀=1.5.

7. I. x⁴+2.5x³–2.51x²–4.473x+3.5802=0; II. l =4.7, s =2.7, v₀=1.4.

8. I. x⁴+4.1x³–4.14x²–0.864x+1.9872=0; II. l =4.8, s =2.8, v₀=1.3.

9. I. x⁴+2x³–2.61x²–7.328x+3.4048=0; II. l =4.9, s =2.9, v₀=1.2.

10. I. x⁴+3.9x³–4.23x²–0.222x+1.0404=0; II. l =5.0, s =3.0, v₀=1.1.

Порядок выполнения работы

1. Получить допуск к работе.

2. Подготовить данные для ввода в ПЭВМ.

3. Отделить вещественные корни уравнения.

4. Найти вещественные корни уравнения, используя функцию root.

5. Найти комплексные корни, используя команду polyroots.

6. Найти размеры ящика объема v₀, максимального объема.

7. Составить отчет о проделанной работе.

Содержание отчета

1. Тексты задач.

2. Графическое решение уравнения.

3. Обоснование отсутствия вещественных корней, кроме отделенных.

4. Данные ввода в ПЭВМ.

5. Результаты счета на ПЭВМ.

6. Интерпретация полученных результатов.

Лабораторная работа № 3

Численное интегрирование

Литература: [1, гл.2, §2; 2, ч.2, гл. §1,4; 6, гл.2, §15; 8, гл.XVI, §1; 11, разд.2, п.4, примеры 10, 11; 19, гл.I, §1.5^*, гл.II, §2.3, п.4].

Постановка задачи. Вычислить приближенно с точностью e>0 определенный интеграл

, (3.1)

где f(x) – непрерывная и дифференцируемая достаточное число раз на отрезке [a,b] функция.

Как известно [19, гл.1, §1.5^*], существуют непрерывные функции, интегралы от которых не выражаются через элементарные функции и, следовательно, использование формулы Ньютона-Лейбница невозможно. В этом случае используются так называемые квадратурные формулы (см.[19, гл.II, §2.3, п.4°]) приближенного вычисления интеграла (3.1). В основании этих формул лежит геометрический смысл определенного интеграла: если подынтегральная функция f(x) непрерывна и неотрицательна на отрезке [a, b], то интеграл (3.1) равен площади S криволинейной трапеции, ограниченной линиями y=f(x)³0, y=0, x=a, x=b(a<b), (рис.3.1).

Рис. 3.1

Вычисление S осуществляется приближенно: на отрезке [a,b] подынтегральная функция f(x) заменяется функцией j(x) и

Функция j может быть либо ступенчатой ломаной, либо вписанной ломаной, либо кусками парабол. Соответствующие формулы поэтому называются формулами прямоугольников, трапеций и Симпсона.

• Формула прямоугольников. Отрезок [a,b] разбиваем на n частей точками x_i=x_o+i∙h, где x_o=a, x_n=b, i=0,1,2,...,n (рис.3.1). Обозначим

(3.2)

Величина h называется шагом интегрирования. В точках x_i, i=1,2,...,n вычисляем значения функции f(x) y_i=f(x_i), i=1,2,...,n. Функцию f(x) считаем непрерывно дифференцируемой на отрезке [a,b].

Таким образом, криволинейная трапеция разбивается на n прямоугольных полос шириной h и высотой y_i, i =1,2,...,n. Площадь i–й полосы будет равна y_i×h, а площадь S криволинейной трапеции составит:

, (3.3)

где (3.4)

- абсолютная погрешность, возникающая из-за замены функции f(x) на ступенчатую функцию j(x).

Формула (3.3) называется формулой прямоугольников с избытком. Если в качестве высоты каждого прямоугольника выбрать левую ординату, по аналогии с (3.3) можно получить формулу прямоугольников с недостатком. Точное значение S будет тогда заключено между значениями, полученными по формулам прямоугольников с недостатком и избытком соответственно.

• Формула трапеций. Пусть функция f(x) дважды непрерывно дифференцируема на отрезке [a,b]. Точки (x_i‑1;y_i-1), (x_i;y_i), i=1,2,...,n (рис. 3.1) соединим отрезками прямой линии (рис. 3.1).

Тогда площадь i-й полосы будет равна площади трапеции (y_i-1+y_i), y_i=f(x_i), i=1,2,...,n и интеграл (3.1) вычисляется по формуле:

(3.5)

где . (3.6)

• Формула Симпсона (формула парабол). Разобьем отрезок [a,b] на четное число частей n=2k, k=1,2, ... . Предположим, что функция f(x) четыре раза непрерывно дифференцируема на отрезке [a,b].

На каждом отрезке двойной длины [x_i-1, x_i+1], i=1,3,5, ... ,2k-1 подынтегральную функцию f(x) заменяем квадратичной функцией j(x) – параболой, проходящей через три точки:

(x_i-1,y_i-1), (x_i,y_i), (x_i+1,y_i+1), y_i=f(x_i), i=1,3,...,2k-1.

Оказывается, что площадь S₁ полосы [x_o,x₂] шириной 2h, ограниченная сверху параболой y=Ax²+Bx+C, снизу - прямой y=0, с боков - прямыми x=x_o, x=x₂, приближенно равна:

Точно также для следующей полосы шириной 2h находим

Продолжая аналогично, найдем площадь последней полосы:

Складывая последние соотношения почленно, получим формулу Симпсона:

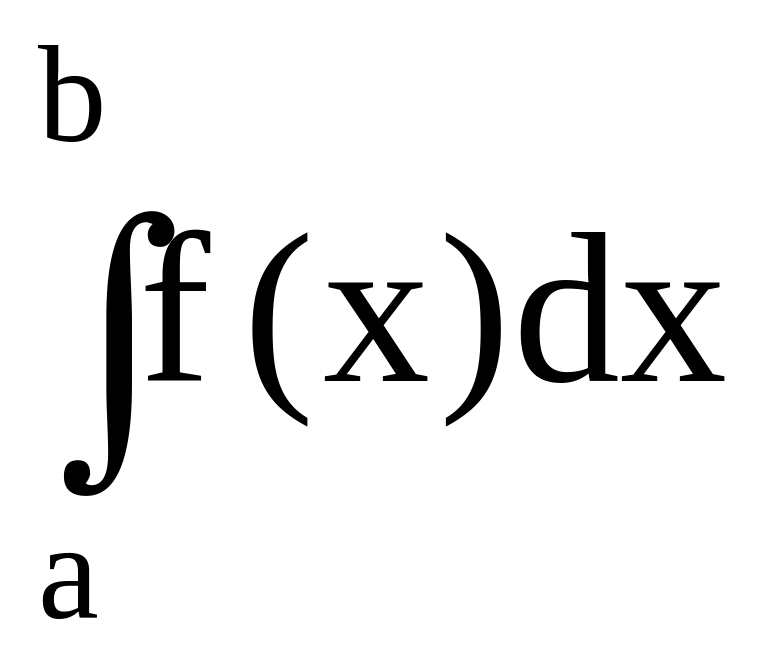= [y_o+2(y₂+y₄+...+y_2k-2)+4(y₁+y₃+...+y_2k-1)+y_2k]+R_n (3.7)

с абсолютной погрешностью

, n=2k (3.8)

При одном и том же значении n формула Симпсона дает наименьшую погрешность. В самом деле, учитывая (3.2), из (3.4), (3.6), (3.8) получаем последовательно

, ,

Иными словами, с увеличением n погрешность формул прямоугольников, трапеций и Симпсона уменьшается пропорционально 1/n, 1/n², 1/n⁴ соответственно.

Чтобы не находить максимум модуля производной соответствующего порядка функции f(x) на отрезке [a,b], на практике используется прием двойного пересчета. Искомый интеграл вычисляется дважды: при делении отрезка [a,b] на n частей (обозначим его через I_n) и при делении отрезка [a,b] на 2-n частей (интеграл I_2n).

Пусть требуется вычислить интеграл (3.1) с точностью e>0. Будем считать, что достигнута требуемая точность, если выполняется неравенство |I_2n - I_n| < e. Тогда I_2n принимаем за приближенное значение интеграла. Для приближенного вычисления определенного интеграла в системе MathCAD 6.0⁺надо (см. 6.1.2): определить функцию и вычислить значение интеграла .

Пусть, вдобавок, требуется найти точку x, для которой =kF(b),

где k и b – заданные числа, xÎ(a;b). Тогда дополнительно определяем функцию

G(x)= , (3.9)

присваиваем k:=k₀; находим (см. §2) корень уравнения G(x)=0: root (G(x), x)=0.

Пример 3.1. Какую работу нужно произвести, чтобы насыпать кучу песка? Куча имеет форму тела, полученного вращением кривой y³=–x⁵32+1, xÎ[;2] вокруг оси ординат. Плотность песка r=2 кг/л. Песок поднимают с поверхности земли, на которой покоится основание кучи. Определить промежуточную высоту h кучи песка такую, чтобы затраченная работа находилась в соотношении 2:1.

Решение. Определим высоту H всей кучи песка. Поскольку основание кучи покоится на поверхности земли, то из уравнения y³=-x⁵32+1 при x= находим y=H=1(рис. 3.2).

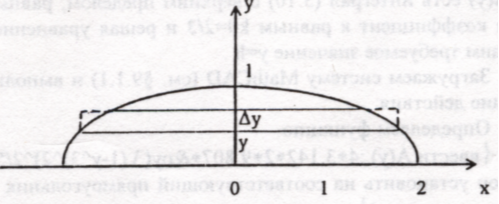
Рис. 3.2

Величина работы A, затраченная на поднятие тела массы m, зависит от высоты y подъема A=m×g×y. Работа, необходимая, чтобы насыпать кучу песка высотой y, есть функция A(y).

При увеличении высоты y на Dy объем песка увеличивается на величину

DV=p∙4∙ ∙Dy

(объем цилиндра высотой Dy с основанием 2∙ ), а затраченная при этом работа увеличивается на величину

DA=DV∙r∙g∙y=4p∙ ∙Dy∙r∙g∙y.

Заменяя приращения дифференциалами, получаем, что искомая суммарная работа выразится интегралом в пределах от y=0 до y=H.

A(H) = 4prg ∙ydy (3.10)

Во второй части задачи нужно найти значение y=hÎ(0;H) такое, чтобы соответствующее значение работы составляло 2/3 суммарной работы. Учитывая (3.9), определим функцию

G(y) = A(y)–kA(H), (3.11)

где A(y) – есть интеграл (3.1) с верхним пределом, равным y. Полагая коэффициент k равным k=2/3 и решая уравнение G(y)=0, находим требуемое значение y=h.

Решение на ПЭВМ. Загружаем систему MathCAD (см. §6.1.1) и выполняем следующие действия:

Определяем функцию вычисления работы A(y) (2кг/л=2000кг/м³)

A(y)=4π∙2000∙9,807

{¨A(y):4CtrlP*2000*9,807*&(1-y^3)^2/5­­­*yTab0TabyTaby¿}.

Вычисляем полную работу А(1), необходимую для насыпания кучи песка {¨А(1)=}.

Cледовательно, А(1)= 95790 (Дж).

Для определения промежуточной высоты hÎ(0;H) вводим функцию (3.11), где k=2/3, H=1:{¨G(y):A(y)–2/3­*A(1) ¿}.

Т.к. 0<y<1, начальное значение корня y уравнения G(y)=0 полагаем равным y=0,5 {¨y:0.5¿}. С помощью функции root находим требуемое значение y=h {¨h:root(G(y),y)¿} {¨h=}.

Итак, h=0.748 (м).

Выполним проверку {¨A(0.748)/A(1)=}.

Документ с решением примера 3.1 приведен на рис. 3.3.

Рис. 3.3

• Ответ. А=95790 (Дж), h=0.667 (м).