
- •Рабочая учебная программа дисциплины «Численные методы в инженерных расчетах»
- •1. Цель и задачи дисциплины
- •1.2. Задачи изучения дисциплины.
- •2. Содержание дисциплины.
- •2.1. Введение.
- •Раздел 1. Теория погрешностей. Вычислительные алгоритмы.
- •Раздел 2. Численное решение нелинейных уравнений.
- •Раздел 3. Численное решение систем уравнений.
- •Раздел 4. Интерполирование и приближение функций.
- •Раздел 5. Решение разностных уравнений.
- •Раздел 6. Численное дифференцирование интегрирование функций.
- •Раздел 7. Численные методы решения обыкновенных дифференциальных уравнений.
- •Раздел 8. Численные методы решения уравнений с частными производными.
- •Раздел 9. Статистическое моделирование и обработка экспериментальных данных.
- •Раздел 10. Пакеты прикладных программ по вычислительной математике.
- •3. Виды работ с распределением времени.
- •4. Перечень тем лекционных и практических занятий.
- •5. Перечень тем, которые студенты должны проработать самостоятельно.
- •6. Перечень лабораторных работ.
- •7. Перечень контрольных работ
- •8. Информационно-методическое обеспечеие дисциплины
- •8.1. Основная литература
- •8.2. Дополнительная литература
- •8.3. Перечень компьютерных программ.
- •9. Краткие методические рекомендации самостоятельной работы по дисциплине.
- •Задание на контрольную работу.
- •Методические указания для студентов
- •Виды работ с распределением времени
- •Перечень тем лекционных и практических занятий
- •Перечень тем, которые студенты должны проработать самостоятельно
- •Перечень лабораторных работ
- •Задания и методические указания по выполнению лабораторных работ для студентов-заочников 3 курса всех инженерно-технических специальностей (кроме 330200 эк, 330100 бжт). Введение
- •Лабораторная работа № 1 Приближенные вычисления.
- •Контрольные вопросы
- •Задание к лабораторной работе №1
- •Порядок выполнения работы
- •Содержание отчета
- •Лабораторная работа № 2 Решение уравнений с одной неизвестной
- •Задания к лабораторной работе № 2
- •Контрольные вопросы
- •Задание к лабораторной работе № 3
- •(Перед каждым двузначным числом таблицы подразумевается ноль с запятой, например: 0,10; 0,09; 0,73...)
- •Организация вычислений на пэвм с помощью
- •Контрольные вопросы
- •II. Подбор эмпирических формул Постановка и решение задачи
- •Контрольные вопросы
- •Задания к лабораторной работе № 5
- •Порядок выполнения работы
- •Содержание отчета
- •Методические указания по работе с системами
- •6.1.1. Управление системой.
- •Функциональные и специальные клавиши:
- •Ввод и редактирование выражений.
- •Редактирование формул.
- •Вставка текста.
- •6.1.2. Операторы и встроенные функции.
- •6.1.3. Простейшие вычисления.
- •6.1.4. Построение графиков.
- •6.1.5. Векторные и матричные операции.
- •6.1.6. Символьные операции.
- •6.1.7. Решение уравнений и систем.
- •6.1.8. Функции линейной и сплайн интерполяции.
- •Методические указания для преподавателей
- •Вопросы к дифференцированному зачету по дисциплине
- •Тесты промежуточного контроля по дисциплине «Численные методы в инженерных расчетах»
- •Тема 3: Интерполирование и приближение функций
- •Тема 4: Численное решение обыкновенных дифференциальтных уравнений.
- •Билеты и задачи для дифференцированного зачета по дисциплине «Численные методы в инженерных расчетах»
- •Задачи к билетам
Тема 3: Интерполирование и приближение функций
Задача интерполяции состоит в следующем:
1) вычислить приближенно с точностью ε > 0 определенный интеграл
![]() ,
где f(x) –
непрерывная и дифференцируемая
достаточное число раз на отрезке [a,b]
функция
,
где f(x) –
непрерывная и дифференцируемая
достаточное число раз на отрезке [a,b]
функция
2). надо построить функцию у = φ(х) которая была бы достаточно близкой на отрезке [x0,xn] к функции y1 = f(x) и просто вычислялась, т.е. φ(х) ≈ f(x) , х ≠ хi
3)Найти решение дифференциального уравнения первого порядка y’=f(x,y) удовлетворяющее начальному условию у(х0)=у0
Ответ 2
2. Формула линейной интерполяции имеет вид:
1)
![]() ,
для любого х
[хi,xi+1]
,
для любого х
[хi,xi+1]
2)![]()
3)![]()
4)![]() ,
i = 0,1,2…
,
i = 0,1,2…
Ответ 1
3.Сплайном называется:
функция, которая вместе с несколькими производными непрерывна на всем заданном отрезке [х0,xn] , а на каждом частичном отрезке [хi,xi+1] в отдельности является некоторым алгебраическим многочленом;
Функция φ(х) в виде алгебраического интерполяционного многочлена

Интерполяционная последовательность , которая находится по формуле
, n = 0,1,2,…
Ответ 1
Существование и единственность интерполяционного многочлена обосновывается:
отличием от нуля определителя Вандермонда для системы n+1 уравнений с n+1 неизвестными
![]() , полученной для многочлена
, полученной для многочлена![]()
равенством нулю определителя Вандермонда для системы n+1 уравнений с n+1 неизвестными
, полученной для многочлена
3) условием
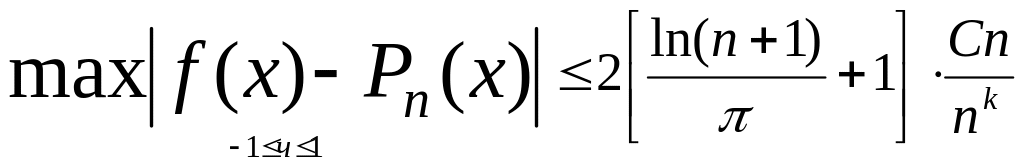 ,
где C = const,
зависящая от m
,
где C = const,
зависящая от m
Ответ 1
Определитель Вандермонда для системы несовпадающих точек
![]()
имеет вид:
1)
![]()
2)
![]()
3)
![]()
Ответ 1
Тема 4: Численное решение обыкновенных дифференциальтных уравнений.
Приближенно решение дифференциального уравнения y’=x2-y2, удовлетворяющее начальному условию у(0)=1, найденному в виде разложения в ряд Маклорена с первыми четырьмя членами , имеет вид:
1)
![]()
2)
![]()
3)
![]()
Ответ 2
По методу степенных рядов точное решение у(х) дифференциального уравнения y’=f(x,y) приближенно представляется в виде:
сходящегося в интервале [a-h, a+h] степенного ряда Тейлора с конечным числом членов:
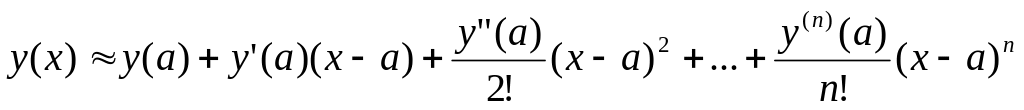
функционального ряда

знакочередующегося ряда

Ответ 1
Постановка задачи при приближенном решении уравнения y’=f(x,y) по методу Эйлера заключается:
1) в каждой из (n+1)
предварительно выбранных точек x0,x1,..xn
точного решения уравнения y’=f(x,y)
находим его приближенное значение yi
(xi)
по формуле:
![]() ,
где
,
где
![]()
2) в каждой из (n+1)
предварительно выбранных точек x0,x1,..xn
точного решения уравнения y’=f(x,y)
находим его приближенное значение yi
(xi)
по формуле:
![]() ,
где
,
где
![]()
в каждой из (n+1) предварительно выбранных точек x0,x1,..xn точного решения уравнения y’=f(x,y) находим его приближенное значение yi (xi) по формуле: , где
Ответ 3
Метод Эйлера основан :
1) на приближенном вычислении призводной
f(xi,yi)
с помощью разностного отношения:![]() , где
, где![]() ,
,
![]() ,
i=0,1,2….n
,
i=0,1,2….n
2) на представлении точного решения по формуле:
3) на повышении точности расчетов по
формуле:
![]()
ответ 1
В практике метода Рунге – Кутта приращения функции
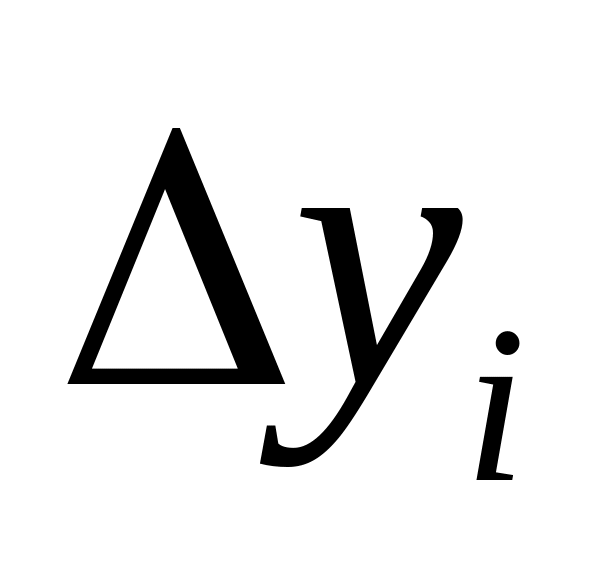 вычисляют
по формуле:
вычисляют
по формуле: ,
где величины чисел k1,k2,k3,k4
находим по формулам:
,
где величины чисел k1,k2,k3,k4
находим по формулам:
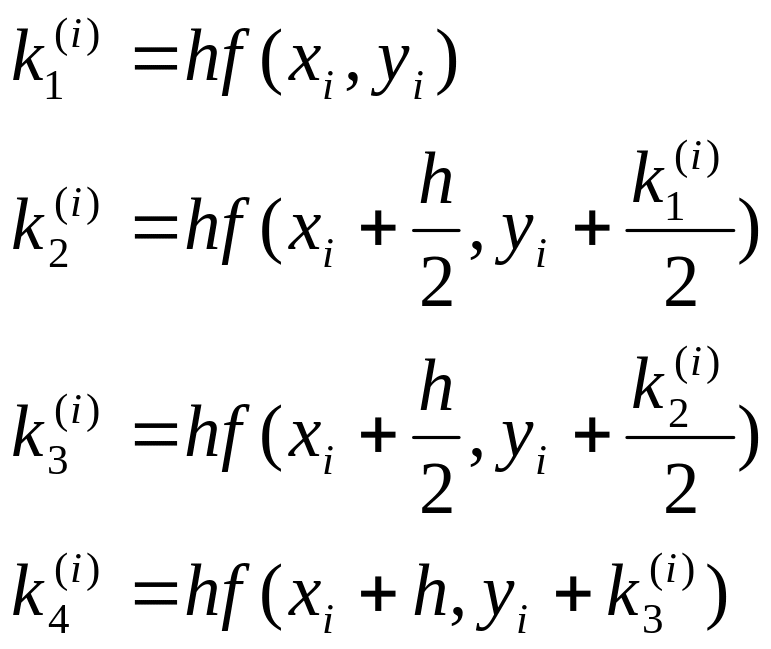
, где величины чисел k1,k2,k3,k4 находим по формулам:

 ,
где величины чисел k1,k2,k3,k4
находим по формулам:
,
где величины чисел k1,k2,k3,k4
находим по формулам:
Ответ 1
6. Для получения приближенного решения дифференциального уравнения y’=f(x,y), у(х0)=у0 по методу Рунге – Кутта целесообразно применять следующую последовательность вычислений:
1) - выбрать шаг вычислений h;
- вычислить числа
![]() при
заданных значениях х0 и у0 и
выбранном значении h;
при
заданных значениях х0 и у0 и
выбранном значении h;
- определить приращение функции
![]() ;
;
- получить значение функции в первой
точке
![]() ,
,
![]() ;
;
- аналогично вычислить числа
![]() в
первой точке при полученных значениях
х1 и у1, приращение функции
в
первой точке при полученных значениях
х1 и у1, приращение функции
![]() и значение функции во второй точке
и значение функции во второй точке![]() ,
,
![]() и т.д.
и т.д.
2) - выбрать шаг вычислений h;
- вычислить числа при заданных значениях х0 и у0 и выбранном значении h;
- определить приращение функции
![]() ;
;
- получить значение функции в первой
точке
![]() ,
,
![]() ;
;
- аналогично вычислить числа в первой точке при полученных значениях х1 и у1, приращение функции и значение функции во второй точке , и т.д.
3) - выбрать шаг вычислений h;
- вычислить числа при заданных значениях х0 и у0 и выбранном значении h;
- определить приращение функции ;
- получить значение функции в первой точке , ;
- аналогично вычислить числа в первой точке при полученных значениях х1 и у1, приращение функции и значение функции во второй точке , и т.д.
Ответ 3
7. Основная идея решения задачи Коши для системы дифференциальных уравнений первого порядка методом Рунге – Кутта заключается в следующей последовательности вычислений:ъ
1)- выбрать шаг вычислений h;
- определить точки вычислений
и в каждой точке вычислить приращение
искомых функций
и
![]() по формулам:
,
по формулам:
,
![]() ,
где
,
где
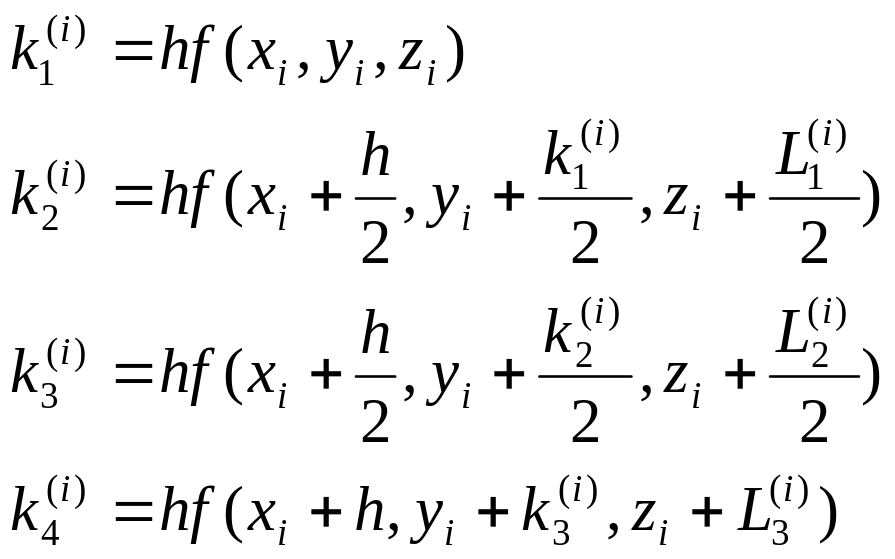
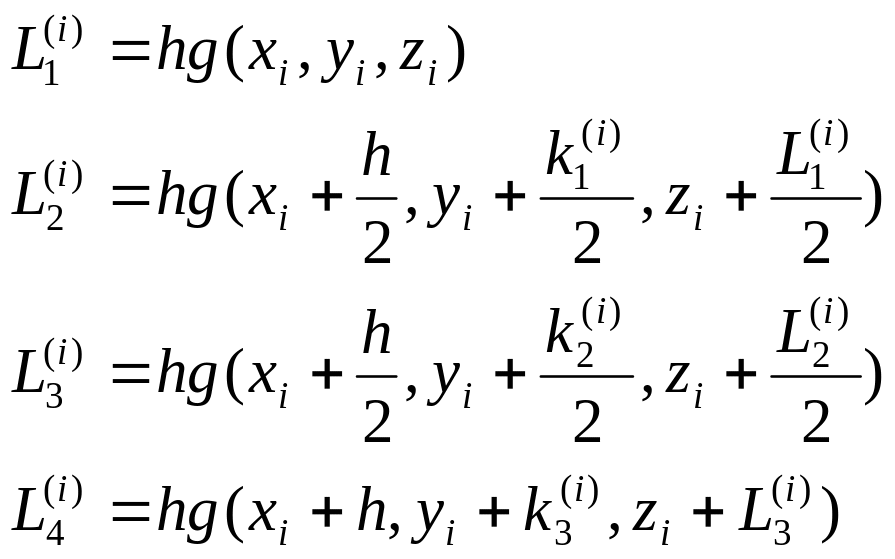
- вычислить значения функций по формулам:
,
![]()
2)- выбрать шаг вычислений h;
- определить точки вычислений
![]() и в каждой точке вычислить приращение
искомых функций
и
по формулам:
,
,
где
и в каждой точке вычислить приращение
искомых функций
и
по формулам:
,
,
где
- вычислить значения функций по формулам:
![]() ,
,
![]()
3) - выбрать шаг вычислений h;
- определить точки вычислений и в каждой точке вычислить приращение искомых функций и по формулам: , , где
- вычислить значения функций по формулам:
![]() ,
,
![]()
Ответ 1
Тема: Решение обыкновенных дифференциальных уравнений и систем операционным методом.
1. Решение обыкновенных дифференциальных уравнений и систем операционным методом основано на применении преобразования функции F(t)f( действительного переменного t R в функцию F(p) комплексной переменной р С с помощью выражения:
1)![]() ;
;
2)
![]() ;
;
3)
![]()
Ответ 1
2. Функция F(p) комплексной переменной р, получаемая с помощью формулы называется:
оригинальным изображением для f(t)
изображением для f(t)
оригиналом для f(t)
Ответ 2
3. Функция f(t) называется оригиналом, если соответствует следующим требованиям:
- f(t)=0 при t<0
-
![]() при
t≥0 , М,
σ – некоторые числа
при
t≥0 , М,
σ – некоторые числа
- f(t) на любом
конечном отрезке [0,![]() ]
имеет не более чем конечное число точек
разрыва первого рода, причем
]
имеет не более чем конечное число точек
разрыва первого рода, причем
 f(t) = f(0)
f(t) = f(0)
- f(t)=0 при t=0
- при 0<t<1 , М, σ – некоторые числа
- f(t) на любом конечном отрезке [0, ] имеет не более чем конечное число точек разрыва первого рода, причем f(t) = f(0)
- f(t)=0 при t>0
- при t≤0 , М, σ – некоторые числа
- f(t) на любом конечном отрезке [0, ] имеет не более чем конечное число точек разрыва первого рода, причем f(t) = f(0)
Ответ 1
4. Интегралом Лапласа называется интеграл вида:
1)
![]()
2)
![]()
3)
![]()
Ответ 3
5. Оригинал функции f(t)=1. Тогда его изображение F(p) имеет вид:
F(p)=
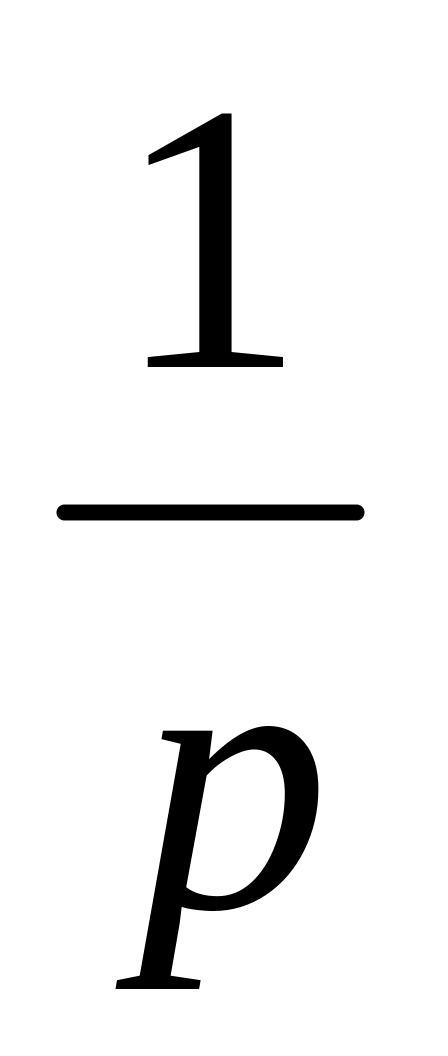
F(p)=1
F(p)=
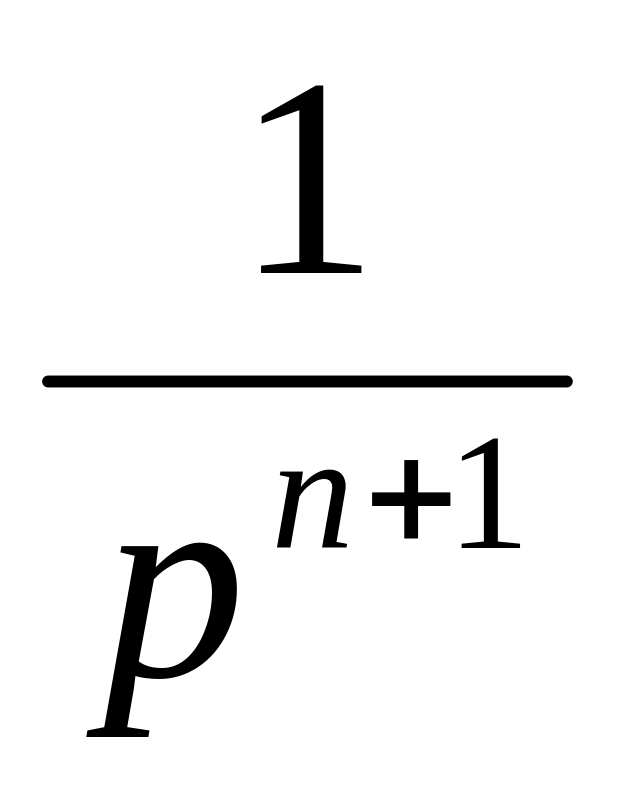
Ответ 1
6. Оригинал функции f(t)=![]() .
Тогда его изображение F(p)
имеет вид:
.
Тогда его изображение F(p)
имеет вид:
1) F(p)=![]()
2) F(p)=
3)F(p)=![]()
Ответ 2
7. Оригинал функции f(t)=
![]() Тогда его изображение F(p)
имеет вид:
Тогда его изображение F(p)
имеет вид:
1) F(p)=![]()
2) F(p)=![]()
3) F(p)=
Ответ 3
8. Оригинал функции f(t)=cosβt . Тогда его изображение F(p) имеет вид:
1) F(p)=![]()
2) F(p)=![]()
3)F(p)=![]()
Ответ 1
9. Оригинал функции f(t)=![]() Тогда его изображение F(p)
имеет вид:
Тогда его изображение F(p)
имеет вид:
1) F(p)=
2) F(p)=![]()
3)F(p)=![]()
Ответ 1
10. Оригинал функции f(t)=![]() Тогда его изображение F(p)
имеет вид:
Тогда его изображение F(p)
имеет вид:
1) F(p)=
2) F(p)=![]()
3) F(p)=![]()
Ответ 2
11. Оригинал функции f(t)=![]() Тогда его изображение F(p)
имеет вид:
Тогда его изображение F(p)
имеет вид:
1) F(p)=
2) F(p)=![]()
3) F(p)=
Ответ 1
12. Оригинал функции f(t)=![]() .
Тогда его изображение F(p)
имеет вид:
.
Тогда его изображение F(p)
имеет вид:
1) F(p)=
![]()
2) F(p)=![]()
3) F(p)=
Ответ 3
13. Изображение f’(t) будет равно:
1) f’(p)
2) p2F(p) - pf(0) – f’(0)
3) pF(p) - f(0)
Ответ 3
14. Изображение f”(t) будет равно:
1) p2F(p) - pf(0) – f’(0)
2) pF(p) - f(0)
3) f”(p)
Ответ 1
15. Изображение y”(t)
– y’(t) –
y(t), если
y(0)=y’(0)=0 и
![]() будет иметь вид:
будет иметь вид:
1)
![]()
2)
![]()
3)
![]()
Ответ 2
16. При решении дифференциального уравнения y” – 2y’- 3y = операционным методом получим
1)![]()
2)
![]()
3)
![]()
Ответ 1
17. Решение системы дифференциальных
уравнений
![]() , найденное операционным методом имеет
вид:
, найденное операционным методом имеет
вид:
1)
![]()
2)
![]()
3)
![]()
Ответ 1
Тема: Статистическое моделирование и обработка экспериментальных данных.
1. Под статистической моделью нормальной случайной величины Х с параметрами М(х) и σ(х) понимают:
1) эмпирический закон распределения выборочных средних квадратических отклонений σb;
2) эмпирический закон распределения выборочных средних хb;
3) эмпирический закон распределения плотности относительных частот нормальной случайной величины Х с выборочным средним хb и выборочным средним квадратическим отклонением σb;
Ответ 3
2.Статистическая модель строится на основе функции Лапласа, которая имеет вид:
1)
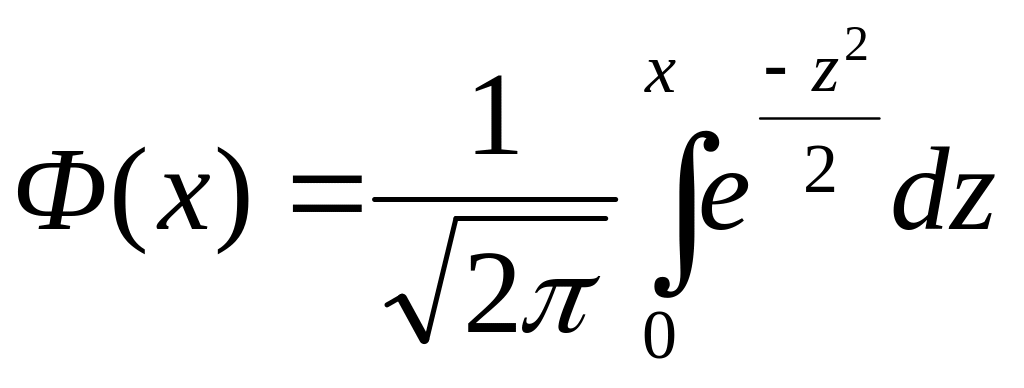
2)
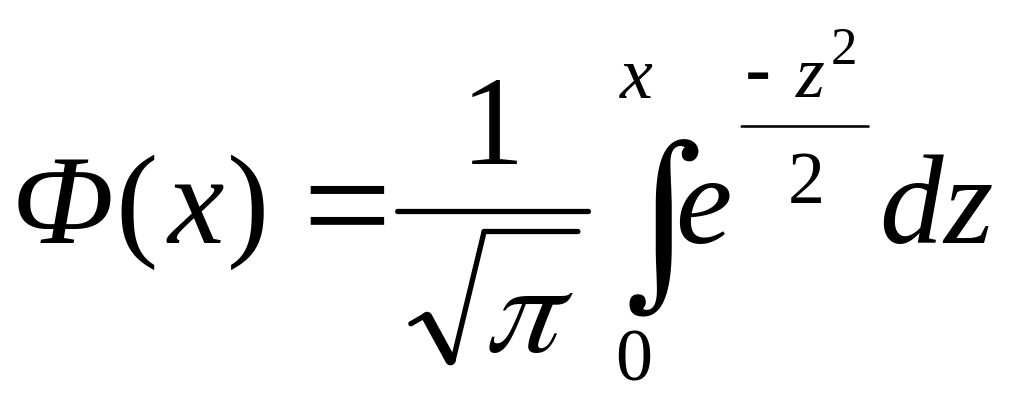
3)
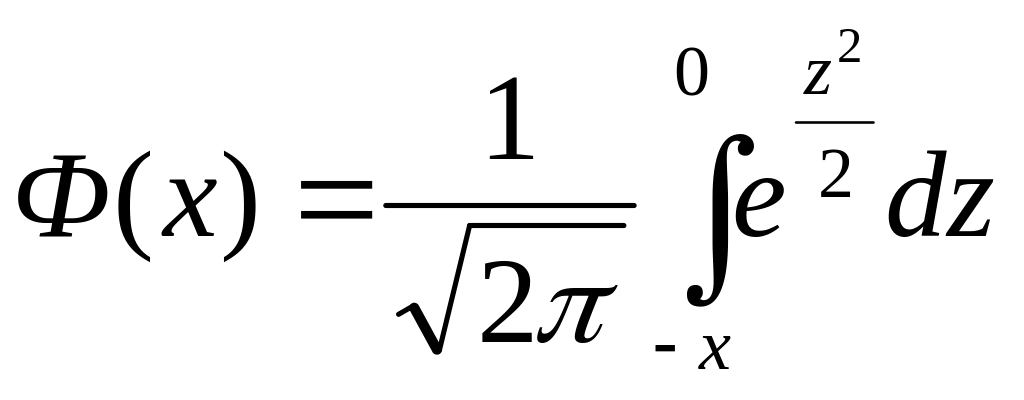
Ответ 1
3.Вероятность попадания нормальной случайной величины в заданный интервал находится по формуле:
1)
![]()
2)
![]()
3)
![]()
Ответ 2
4.Для построения статистической модели нормальной случайной величины Х необходимо с равной вероятностью выбрать 100 значений xi из нормального распределения случайной величины Х при заданных М9х) и σ(х) и произвести статистическую обработку полученной выборки. Каждое значение xi определяется по формуле:
1)![]()
2)
![]()
3)
![]()
Ответ 1
5.Под случайными числами ri понимают:
1) возможные отдельные значения непрерывной случайной величины R, равномерно распределенной в интервале (-∞, 0);
2) возможные отдельные значения непрерывной случайной величины R, равномерно распределенной в интервале (1,+∞);
3) возможные отдельные значения непрерывной случайной величины R, равномерно распределенной в интервале (0,1);
Ответ 3
Тема: Численное интегрирование.
Формула прямоугольников для приближенного вычисления интеграла имеет вид:
1)
![]() ,
где
,
где
![]()
2)
![]() ,
где
,
где
![]()
3)
![]() ,
где
,
где
![]()
Ответ 1
Формула трапеций для приближенного вычисления интеграла имеет вид:
1) , где
2) , где
3) , где
Ответ 2
3. Формула Симпсона для приближенного вычисления интеграла имеет вид:
1) , где
2) , где
3) , где
Ответ 3
Тема : Решение задач линейного программирования.
1. Ограничение задачи линейного программирования имеет предпочтительный вид, если:
1) левая часть ограничения содержит переменную, входящую с коэффициентом, равным нулю, а в остальные ограничения – с коэффициентом, равным единице;
2) левая часть ограничения содержит переменную, входящую с коэффициентом, равным двум, а в остальные ограничения – с коэффициентом, равным единице;
3) левая часть ограничения содержит переменную, входящую с коэффициентом, равным единице, а в остальные ограничения – с коэффициентом, равным нулю;
Ответ 3
2. Переменные являются базисными, если они входят в предпочтительное ограничение с коэффициентом, равным:
1) 1, а в остальные – с коэффициентом, равным 0;
2) -1, а в остальные – с коэффициентом, равным 0;
3) 2, а в остальные – с коэффициентом, равным 1;
Ответ 1
Условие задачи линейного программирования записывается в таблицу, которая называется:
квадратной;
симплексной ;
прямоугольной.
Ответ 2
Из перечисленных правил выберите правила преобразования симплексной таблицы:
1) Чтобы получить элемент
![]() новой
таблицы нужно из соответствующего
элемента прежней таблицы вычесть
величину
новой
таблицы нужно из соответствующего
элемента прежней таблицы вычесть
величину ;
элементы разрешающей строки разделить
на
;
элементы разрешающей строки разделить
на
![]() ;
;
2) Если задача имеет решение, то после некоторого конечного числа шагов придем к тому, что все числа в нулевой строке будут неотрицательными;
3) Выделяя при помощи полученной таблицы предпочтительные переменные (в соответствующем столбце – один элемент равен 1, а остальные 0), находим оптимальное решение;
4) Чтобы получить элемент
новой
таблицы нужно из соответствующего
элемента прежней таблицы вычесть
величину ;
элементы разрешающей строки разделить
на
;
;
элементы разрешающей строки разделить
на
;
5) Если задача имеет решение, то после некоторого конечного числа шагов придем к тому, что все числа в нулевой строке будут равны нулю;
Ответ 1,2,3
