При этом функция давления

Подставляя это выражение в формулу (5.53) и учитывая малое влияние массовых сил, получаем уравнение Бернулли для адиабатного движения идеального совершенного газа

(5.57)

Уравнения (5.56) и (5.57) можно применять при тех же ограничительных условиях, что и интеграл Бернулли, из которого они получены. С практической точки зрения имеет смысл исполь­зовать их лишь в случаях, когда существенно проявляется сжимаемость газа, что имеет место при скоростях, соизмеримых со скоростью звука. Для описания движения газа с малыми скоростями можно пользоваться уравнением Бернулли для несжимаемой жидкости.

3. Неустановившееся безвихревое течение. Для этого случая ди/дt  0 и  = 0. Последнее условие, как известно из кинематики, эквивалентно существованию потенциала скорости , для которого grad  = и.

Поскольку речь идет о неустановившемся движении, то  зависит не только от координат, но и от времени t, которое будем рассматривать как параметр. Тогда уравнение (5.43) можно записать в форме

или, меняя порядок операций д/дt и grad, grad (Е + ) = 0.

Из этого выражения следует, что функция, стоящая под знаком grad, не зависит от координат х, у, z, но это не значит, что она не зависит от времени. Поэтому запишем

где f(t) — произвольная функция времени.

Соотношение (5.58) называется интегралом Лагранжа. Для несжимаемой жидкости (P = р/) в поле силы тяжести (Ф = gz) из выражения (5.58) получаем уравнение

(5.59)

которому можно придать форму, вытекающую из уравнения (5.23) как частный случай. Для этого выберем в некоторый момент времени произвольную трубку тока. Поскольку правая часть уравнения (5.59) зависит только от времени, значения левой части

в данный момент времени должны быть одинаковы в сечениях 1 и 2 трубки (см. рис. 5.2). Поэтому

(5.60)

Если s — криволинейная координата, отсчитываемая вдоль оси трубки тока, то, как известно, и = д/дs, откуда.

где f₂(t)— произвольная функция времени.

Очевидно, f₂(t ) |₁ = f₂(t ) |₂.

Отсюда следует, что

Теперь выражение (5.60) можно записать в виде

(5.61)

Это уравнение, очевидно, есть частный случай уравнения (5.23) при  = 0.

4. Относительное движение идеальной жидкости. Рассмотрим движение жидкости в канале, который перемещается с ускорением относительно Земли. В этом случае движение жидкости относительно стенок канала будем называть относительным. Такое течение имеет место, например, в турбомашинах: оно создается в проточных каналах между лопастями, образующими гидродинамическую решетку (рис. 5.6).

Если это движение рассматривать в системе координат, жестко связанной со стенками канала, то при постоянной во времени относительной скорости движение будет установившимся. Полагая жидкость идеальной, его можно описать уравнениями Эйлера, однако в отличие от абсолютного движения, в соответствии с изве­стным принципом механики, необходимо в число массовых сил ввести силы инерции.

Пусть движение происходит вдоль трубки тока, вращающейся как целое с постоянной угловой скоростью  (рис. 5.7). В число массовых сил должны быть включены: сила тяжести F_g == g центробежная сила F_ц = (v²/r) r⁰ == ²rr⁰, кориолисова сила F_к = – 2 х и, где v =  r – окружная переносная скорость на окружности радиусом r; r⁰ — единичный вектор радиального направления; и — относительная скорость движения вдоль струйки.

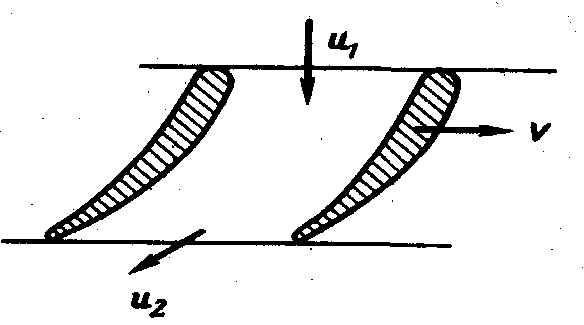
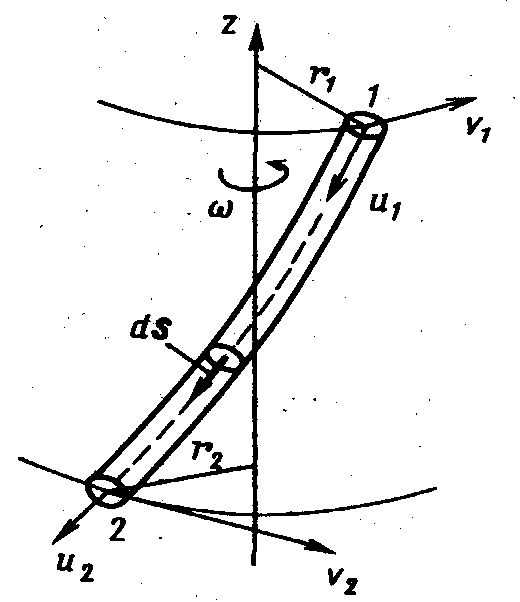
Рис. 5.6. Схема, иллюстрирующая относительное течение жидкости

Рис. 5.7. Схема к выводу уравнения Бернулли для относительного движения в элементарной струйке

Уравнение движения в подвижной (неинерциальной) системе координат согласно выражению (5.40) запишем в виде

(5.62)

Полагая движение установившимся (ди/дt = 0) и безвихревым ( = 0), а также учитывая, что F_g = —grad (gz), F_ц = grad (²r²/2) и (1/) grad p = grad P, получаем

(5.63)

Умножим обе части этого уравнения скалярно на элементарный вектор ds перемещения вдоль оси струйки и учтем, что вектор кориолисовой силы нормален к вектору относительной скорости и т. е. нормален к вектору ds, а значит, F_н ds = 0. Тогда получим

(5.64)

Применяя этот интеграл к двум сечениям 1 и 2 элементарной струйки, учитывая, что (r = v есть переносная скорость, получим уравнение относительного движения тяжелой идеальной жидкости

(5.65)

Для несжимаемой жидкости P = p/ и уравнение (5.65) принимает вид

(5.66)