5.2. Уравнения движения вязкой жидкости (уравнения навье—ctokca*)

Подставив в уравнения движения (3.10) выражения (5.6), получим

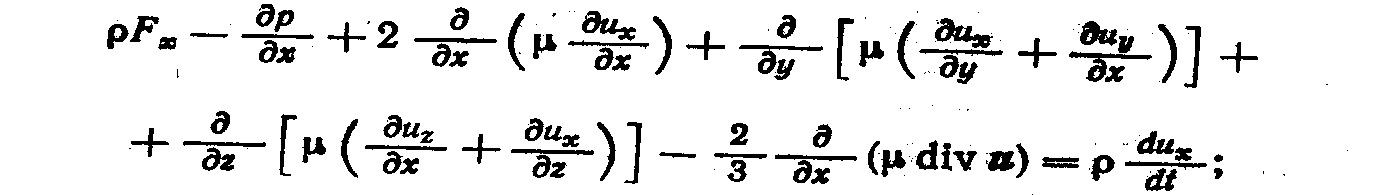
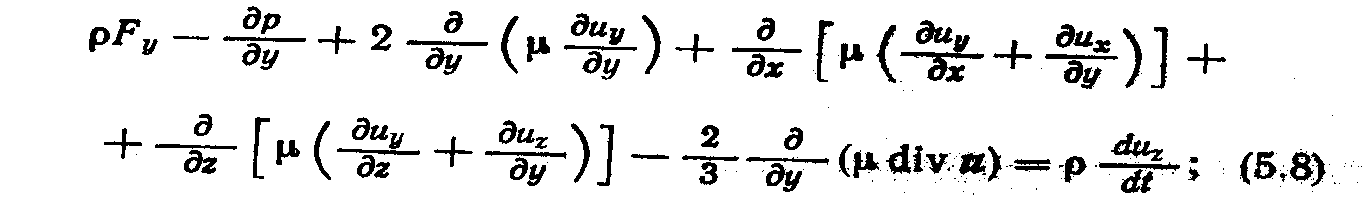
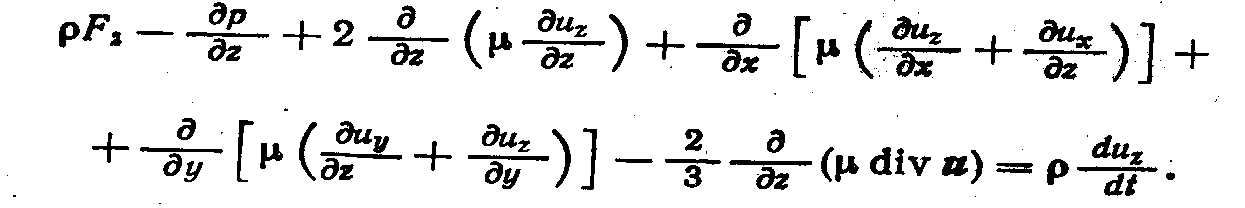
Эти уравнения называются уравнениями Навье — Стокса; их используют для описания движений вязких сжимаемых жидкостей и газов.

Уравнения движения невязких жидкостей и газов легко получить из уравнений Навье — Стокса как частный случай при  = 0; для несжимаемых жидкостей следует принять  = const.

Система уравнений Навье — Стокса незамкнута, так как содержит шесть неизвестных: и_x, и_y, и_z, р,  и . Еще одним уравнением, связывающим эти неизвестные, является уравнение неразрывности

В качестве уравнений, замыкающих систему, используют уравнения состояния среды и зависимости вязкости от параметров состояния. Во многих случаях приходится применять также дру­гие термодинамические соотношения.

Для несжимаемой жидкости (ρ = const) в большинстве случаев вязкость можно считать постоянной, что позволяет значительно

____________________

•Луи Мари Анри Навье (1785—1836) — видный французский инженер и механик, профессор Школы мостов и дорог, а затем Политехнической школы в Париже, член французской академии наук. Первым вывел (в 1824 г.) уравне­ния движения вязкой жидкости.

упростить уравнения (5.8). После простых преобразований, учитывая, что div u = 0, получаем

Если раскрыть полные ускорения dи_x/dt, dи_y /dt, dи_z/dt, выделив в них локальную и конвективную части, то получим развернутую форму уравнений Навье — Стокса для несжимаемой жидкости:

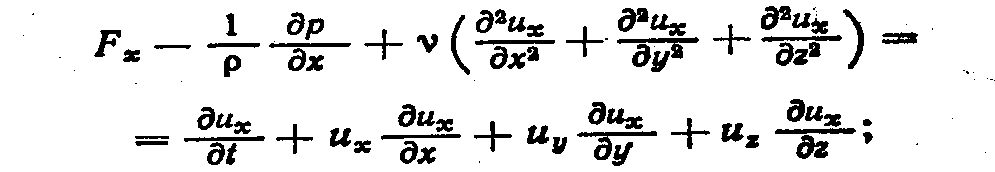
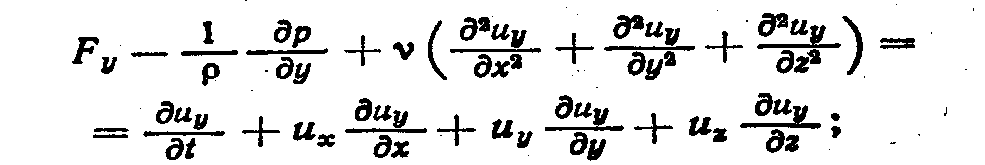(5.9)

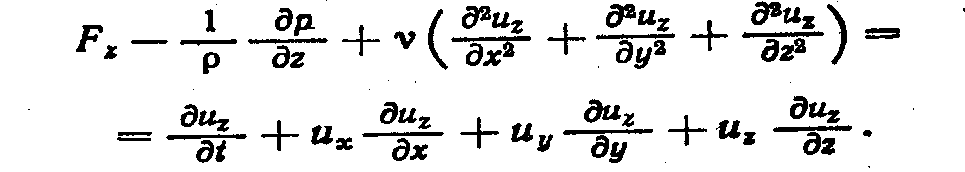
Вместе с уравнением неразрывности div и = 0 уравнения (5.9) образуют замкнутую систему для определения функций и_x, и_y, и_z и р.

Представим уравнения Навье — Стокса в векторной форме. Для этого умножим первое из них на i, второе — на j, третье — на k и сложим. Получим

F - (1/) grad р + ²u = du/dt, (5.10)

где ²u = ²u_x i + ²u_y j + ²u_z k.

Формулы (5.9) или (5.10) могут быть истолкованы как уравнения второго закона Ньютона в форме, специфической для вязкой несжимаемой жидкости. Действительно, их правые части представляют собой отнесенные к единице массы произведения массы на ускорения (единичную силу инерции), а левые — сумму отнесенных к единице массы сил, в числе которых массовая сила

F (F_x, F_y, F_z,), силы давления grad р ( , , )

и вязкости ²u = (²u_x, ²u_y, ²u_z).

Выделяя конвективную часть уравнения (см. п. 1.2), уравнение (5.10) представим в виде

Для получения еще одной употребительной формы уравнения (5.10) используем формулу векторного анализа

где а и b — произвольные векторы.

Правильность этой формулы можно проверить непосредствен­ным вычислением.

Пусть а = b = и. Тогда

где  — rot и.

Разрешая это уравнение относительно конвективного ускорения (u) u и исключая его из формулы (5.11), получаем уравнение Громеки — Ламба ^* движения вязкой жидкости ,

Считая, что массовые силы обладают потенциалом, т. е. F = —grad Ф, и учитывая, что при  = const (1/) grad р = grad (p/), уравнение (5.12) приведем к виду

Уравнения Навье — Стокса в форме (5.13) удобны для решения ряда задач динамики вязкой жидкости.

Во многих задачах течение вязкой жидкости обладает осевой симметрией и его лучше описывать, пользуясь цилиндрической системой координат. Уравнения Навье — Стокса в этой системе имеют вид

_________________________

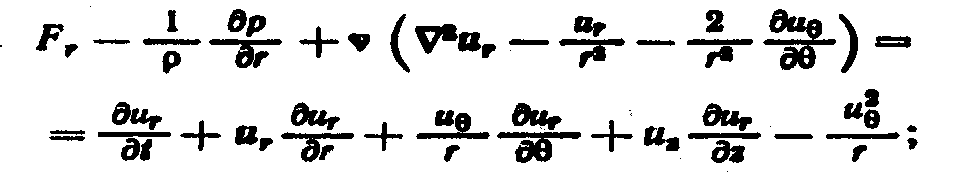
• Громека Ипполит Степанович (1851—1889) — русский физик, профессор Казанского университета, автор многих исследований по гидромеханике (теория винтовых потоков; неустановившееся движение вязкой жидкости в трубах, распространение ударных волн в жидкостях др.).

Вместе с уравнением неразрывности (2.25) уравнения (5.14) образуют замкнутую систему уравнений движения несжимаемой жидкости в цилиндрических координатах.

Общая задача гидромеханики состоит в определении функций: и_x, и_y, и_z, р,  и , с помощью системы уравнений Навье —- Стокса (5.8) или (5.9). уравнения неразрывности (2.14) или (2.16) и до­полнительных соотношений, замыкающих систему. Таким образом, гидродинамическая задача сводится к математической задаче получения решений системы нелинейных дифференциальных урав­нений в частных производных второго порядка. Математическая теория таких систем разработана пока недостаточно и для них нет общей формулировки и доказательства теорем существования и единственности. Однако для частных видов системы (5.9), описывающих определенные классы течений, такие теоремы сформулированы и доказаны.

Поскольку общие решения дифференциальных уравнений в частных производных содержат произвольные функции, для получения конкретных решений нужно их определить. Для этого должны быть заданы начальные и граничные условия, которым удовлетворяют найденные решения.

Под начальными условиями понимают заданные значения искомых функций в начальный момент времени во всей области течения, а под граничными — заданные значения, которые должны принимать искомые функции в точках граничных поверхностей во все моменты времени.

Рассмотрим начальные и граничные условия для неустановившегося движения несжимаемой жидкости ( = const,  = const). В качестве начальных условий задается распределение скоростей, и_x, и_y, и_z в области течения в начальный момент времени t₀:

и_x = f₁ (x, y, z, t₀); и_y = f₂ (x, y, z, t₀); и_z = f₃ (x, y, z, t₀). (5.15)

Задавать давление нет необходимости, так как для момента t₀ его можно определить из исходных уравнений по известным f₁, f₂ ,f₃ . Граничные условия зависят от характера границ. На не­подвижной непроницаемой стенке они заключаются в равенстве нулю на ней скоростей жидкости (и = 0), так как частицы вязкой жидкости прилипают к стенке. Это условие имеет вид

и_x (x, y, z, t₀) = 0; и_y (x, y, z, t₀) = 0; и_z (x, y, z, t₀) = 0,

где x_С, y_С, z_С — координаты точек твердой стенки.

На подвижной непроницаемой границе скорость жидкости совпадает со скоростью движения самой границы. Границей области течения может служить свободная поверхность. Ее форма, а также значения скоростей на ней неизвестны в сформулированные выше кинематические условия

Для установившегося движения локальное ускорение всюду равно нулю. Так как при этом h_c = 0, уравнение (5.23) принимает вид

(5.24)

Это уравнение, называемое уравнением Д. Бернулли, является одним из фундаментальных уравнений гидромеханики. Определим его физический смысл.

Сначала рассмотрим установившееся движение (ди/дt = 0) и перепишем выражение (5.19) в виде

(5.19)

В левой части стоит дифференциал по направлению s величины u²/2, которую называют плотностью кинетической энергии. По существу, u²/2 является кинетической энергией жидкой частицы, отнесенной к единице ее массы. Величина —d_sФ есть дифференциал потенциала массовой силы, который, как известно из общей механики, является элементарной работой этой силы. Чтобы истолковать величину d_sp/(g), рассмотрим живое сечение dS элементарной трубки тока, для которого скорость жидкости равна и, а давление равно р (рис. 5.3).

Если за время dt частицы, расположенные в этом сечении, переместились на расстояние udt, то работа силы давления pdS на этом пути будет равна pdSudt. Отнеся эту работу к массе жидкости в объеме dSudt, найдем, что величина р/ представляет собой работу сил давления, отнесенную к единице массы. Последний член уравнения (5.19') представляет собой работу удельной (т. е. отнесенной к единице массы) силы вязкости v²u на элементарном пути ds. Заметим, что этим членом учитывается работа как внутренних, так и внешних вязкостных напряжений.

Таким образом, уравнение (5.19') выражает теорему живых сил для бесконечного малого объема жидкости: дифференциал удельной кинетической энергии равен сумме элементарных удельных работ всех внутренних и внешних массовых и поверхностных сил, действующих на жидкость данного объема.

Теорема живых сил, вытекающая из уравнений движения, выражает баланс механической энергии, а для идеальной жидкости ( = 0) — частный случай закона сохранения энергии.

Переходя к конечной форме уравнения [см. (5.24)], представим его в виде

(5.24)

где все члены отнесены к единице веса и имеют линейную размерность. Из уравнения (5.24') следует, что изменение удельной кинетической энергии равно сумме удельных работ силы тяжести

(z₁ — z₂), давления (p₁—p₂)/( g) и вязкости (–h`_c), т. е. это уравнение выражает в конечной форме теорему живых сил.

Для общего случая неустановившегося движения получено уравнение (5.23), в которое входит член h_i, называемый инерционным напором. Как видно из выражения (5.22), он зависит от локального ускорения ди/дt и, как можно показать, выражает специфические для неустановившегося движения обратимые преобразования энергии. Подробнее об этом изложено в гл. 6.