5.12. Метод размерностей

Уравнения, связывающие параметры гидродинами­ческих процессов, выражают те или иные физические законы и потому их структура не должна зависеть от системы единиц измерения. Учитывая это обстоятельство и принимая во внимание возможность применять для описания гидродинамических (так же как и для других физических) процессов разнообразные, в том числе специально выбранные системы единиц, можно установить некоторые общие свойства указанных уравнений. Знание этих свойств позволяет во многих случаях прогнозировать структуру искомых связей между физическими размерными и безразмер­ными параметрами. Используя формулу размерности (предпо­лагается, что она известна читателю из курса физики), можно указать также рациональные комбинации физических параметров, определение связей между которыми, дает результаты, относя­щиеся, сразу к целому классу явлений. Совокупность этих, а также некоторых других, с ними связанных, вопросов составляет теорию размерностей, которая особенно полезна на первых стадиях изучения явления, когда еще отсутствует достоверное математи­ческое описание.

Рассмотрим зависимость

(5.90)

которая выражает функциональную связь между размерной величиной q и размерными, не зависящими одна от другой величинами l, t, т…

Установим общую структуру функции f (l, t, ...), предполагая, что она описывает некоторый физический (в частности, гидродинамический) закон. Допустим, что из числа величин l, t, т, ..., w первые три, т. е. l, t и m, имеют независимые размерности, т. е. формула размерности любой из этих величин не может быть представлена как комбинация формул размерности двух других*.

__________________

• В качестве величия l, t и т с независимыми размерностями могут быть взяты не обязательно величины с простыми размерностями, как, например, длина, время и масса. Вместо времени может быть взята скорость или ускоре­ние, вместо массы — плотность, вместо длины — произведение скорости на время и т.п.

Заметим, что все нижеследующие рассуждения остаются справедливыми и в том случае, если величин с независимыми размерностями будет не три, а сколько угодно.

Если величинами l, t, т, которые условимся называть основ­ными, исчерпывается число величин с независимыми размерно­стями, то размерности остальных величин v, а, ... можно выразить через размерности l, t, т. Так, если L, Т и М соответственно единицы измерения для l, t и т, то формулами размерности будут

Изменим теперь единицы измерения основных величин соот­ветственно в  _l, _t и _т раз, т. е. перейдем к единицам

Тогда величины q, l, t, т, v ... в уравнении (5.90) будут выра­жаться в этих новых единицах, но вид уравнения не должен изме­ниться, так как оно описывает, по предположению, некоторый физический закон, который не может зависеть от выбора системы единиц. Поэтому в новых единицах вместо уравнения (5.90) можем записать

(5.91)

Величины q₁, l₁, t₁, .... выраженные в новых единицах L₁, T₁, и M₁, связаны с их значениями в старых единицах соотношениями

Выражение (5.91) можно переписать в виде

Поскольку масштабы  _l, _t, и _т единиц измерения основных величин произвольны, то, в частности, их можно выбрать так, чтобы

При этом фактически за единицы измерения принимаются основные величины l, t и т, входящие в уравнение (5.90). Тогда формула (5.91) перейдет в следующую:

Входящие в это уравнение комплексы

являются, очевидно, безразмерными. Вводя для них соответству­ющие обозначения _q,_v,_a..., приходим к уравнению

(5.92)

или в более компактной записи

(5.93)

Обобщая полученный результат для произвольного числа величин, входящих в исходное уравнение (5.90), можно сформу­лировать следующую теорему.

Выражающую некоторый физический закон, функциональную зависимость между n = k + s размерными величинами, из которых k величин, имеют независимые размерности, можно представить в виде зависимости между п — k безразмерными комплексами _i;(i = q, t, v , ...), каждый из которых является комбинацией из k + 1 размерных величин.

Эта теорема, получившая название  -теоремы, является основ­ной в теории размерностей и в то же время входит в число трех основных теорем теории подобия. Ее роль в теории подобия определяется тем, что безразмерные комплексы _i, представляют собой критерии подобия и, следовательно, уравнение (5.93) дает связь между ними.

 -теорема имеет общефизический характер. Для приложения этой теоремы к задачам прикладной гидромеханики следует конкретизировать встречающиеся в них механические величины; и их безразмерные комбинации. Так, при описании движения вязкой упругой жидкости встречаются три группы величин:

1) геометрические параметры, характеризующие размеры и формы граничных - поверхностей —l₁,l₂,l₃, ...;

2) кинематические и динамические характеристики течения — скорость и (или расход Q), давление р (или его градиент dp/dx), касательное напряжение , сила сопротивления F_с;

3) характеристики физических свойств жидкости — плот­ность , динамический коэффициент вязкости , модуль упругости Е, коэффициент поверхностного натяжения .

Приведенный перечень параметров не является обязательным, его можно расширить, а некоторые из параметров заменить дру­гими. Например, вместо динамического коэффициента вязкости можно ввести кинематический коэффициент  = /. Геометри­ческими параметрами могут быть углы, определяющие конфигура­цию границ или поля течения. Как правило, искомой исследу­емой величиной является параметр второй группы, т. е. кинема­тическая или динамическая характеристика потока, которую нужно определить как функцию всех или части остальных пара­метров. Следует подчеркнуть, что составление полного перечня параметров, определяющих исследуемый процесс, является важ­ной частью решения задачи методом размерностей. Оно упро­щается, если процесс описан математически, в частности диффе­ренциальными уравнениями; в противном случае необходимо иметь четкое представление о физической сущности процесса, основанное на предварительном экспериментальном изучении. Для применения метода размерностей, как правило, необходима

схематизация явления, подобная той, какая применяется для математического описания.

В качестве параметров с независимыми размерностями в гидро­механике обычно выбирают характерные длину l, скорость v и плотность , которые входят в каждую из безразмерных комби­наций _i.

Составим безразмерные комбинации _i для линейных размет ров l , а, b, характерной скорости v , плотности  жидкости, перепада р давления, касательного напряжения , ускорения g свободного падения, динамического коэффициента вязкости  поверхностного натяжения , модуля упругости жидкости E.

Поскольку параметров с независимыми размерностями всего три (l, v и ), k = 8, п = 11. Следовательно, необходимо получить восемь безразмерных комплексов_i. Согласно общей формуле

Так как _а безразмерная величина, очевидно, х_а = 1, y_a = 0, z_a = 0. Следовательно, _а = a/l. Аналогично _в = b/l. Тогда

Необходимые показатели степени х_p , y_p , z_p проще всего по­добрать, записав размерность _p в виде [_p] = L⁰T⁰M⁰ (где L⁰, Т⁰ и М⁰—единицы длины, времени и массы) и сравнив с ней размерности правой части последнего равенства. Так как

получим

Приравняем показатели степеней при одноименных величинах в левой и правой частях:

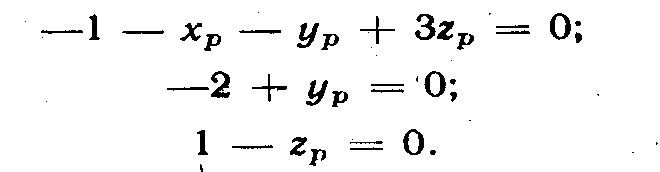
Решая эту систему, находим х_p == 0; y_р = 2; z_p = 1. Следова­тельно,

Аналогично определяем остальные безразмерные комбинации _i:

Безразмерные параметры _а и _b очевидно, характеризуют геометрию потока, _р—число Эйлера Еu; 1/_gи 1/_ —соот­ветственно числа Фруда и Рейнольдса. Параметр _ выражает в безразмерном виде напряжение, обусловленное силами трения;

величину С_f = 2_ называют обычно коэффициентом трения. Величины

называют соответственно числами Вебера и Коши; они характе­ризуют действие в жидкости сил поверхностного натяжения и упругости. Полученный результат можно представить в форме

или

Любой из безразмерных параметров этих функций можно рассматривать как зависимый, а остальные как аргументы, но чаще всего искомыми величинами являются Еu или С_f.

Метод размерностей не дает возможности установить в кон­кретных случаях вид функции , однако знание даже общей зависимости, выражаемой уравнением (5.94), полезно как для теоретического анализа, так и для рациональной постановки эксперимента.

Рассмотрим несколько примеров использования метода раз­мерности в конкретных задачах.

Пример I. Определение сопротивления движению несжимаемой жидкости в цилиндрических трубах. Рассмотрим течение вязкой несжимаемой жидкости в круглой цилиндрической гладкой трубе. Пусть задача состоит в нахождении структуры зависимости падения давления р на участке длиной l от параме­тров системы.

Из предыдущего известно, что из-за отсутствия свободной поверхности числа Фруда и Вебера не влияют на характер движения, а значит, и на искомую за­висимость. Так как жидкость несжимаема, на нее не влияет также и число Коши. Из геометрических параметров для труб с гладкими стенками можем указать только два: длину l участка и диаметр d трубы. Считаем известным, что при дви­жении заданной жидкости (параметры  и ) по трубе фиксированного диаметра устанавливается однозначное соответствие между характерной скоростью v и падением давления р на участке длиной l. При этом, разумеется, устанавли­вается и определенное значение касательного напряжения , но оно вполне опре­деляется перепадом р и потому не может служить независимым параметром, С учетом этих соображений к параметрам, определяющим явление, отнесем l, d, v , р, . Из этих шести размерных параметров можно составить всего три π-параметра:

поэтому искомая связь должна иметь вид

или, если принять р /(р²) за функцию, то она будет зависеть от двух безразмерных аргументов:

Так как граничные условия вдоль трубы не изменяются (постоянный диа­метр, гладкая поверхность), естественно предположить линейную зависимость р от l. Опыт подтверждает это предположение. Поэтому последнюю связь можно представить в виде

Введя обозначение = 2_, получим

(5.95)

Формула (5.95) впервые была получена эмпирическим путем и является основной расчетной формулой для гладких труб. Эксперимент и теоретические решения хорошо подтверждают наличие функциональной зависимости  (Re).

Для шероховатых труб в число параметров надо включить линейную ха­рактеристику неровностей стенки  (например, среднюю высоту выступа). Тогда к рассмотренным -параметрам добавляется еще один /d. Проводя аналогичные рассуждения, находим

= (Re, /d ).

Экспериментальные данные четко подтверждают наличие такой связи. Обратим внимание на то, что связь между р /(²) и его аргументами можно записать в критериальной форме

или для шероховатых труб

Параметры l/d и /d обеспечивают геометрическое подобие потоков в трубах разных диаметров, длин и шероховатостей и имеют одинаковое значение для всех геометрически подобных труб. Из соотношения (5.96) следует, что число Эйлера является функцией числа Рейнольдса и для напорного (закрытого) по­тока не может служить определяющим критерием подобия. Иными словами, механическое подобие таких потоков обеспечивается геометрическим подобием и критерием Рейнольдса.

Пример 2. Определение сопротивления трению продольно обтекаемой пластины. Пластину длиной l обтекает безграничный поток вязкой несжимаемой жидкости, вектор скорости которого и₀ параллелен плоскости пластины. Вдоль направления u₀ направим ось х. Считая течение плоским, попытаемся найти зависимость для касательного напряжения τ в некоторой точке пластины, харак­теризуемой координатой х. Величина τ должна зависеть от этой координаты и не зависеть от полной длины l пластины. Давление вдоль пластины не изменяется, и, следовательно, к параметрам явления относятся х, и₀, , τ, . Из этих пяти величин можно образовать только два -параметра:

связь между которыми

определит искомую зависимость

Рис. 5.11. Истечение жидкости под давлением через отверстие в стенке резервуара

Структура этой зависимости полностью согла­суется с результатом приближенной теории погра­ничного слоя, согласно которой

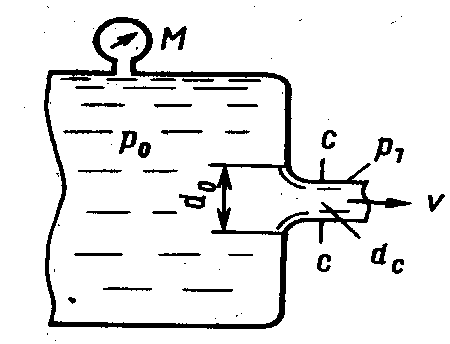
Пример. 3 Истечение жидкости под давлением через отверстие в стенке резервуара. Пусть несжимаемая жидкость вытекает из резервуара, в котором она находится под давлением р₀, в среду с давлением p₁ через круг­лое отверстие диаметром d₀ (рис. 5.11). Перепад давления р = р₀—p₁ при­мем достаточно большим, чтобы можно было не учитывать силу тяжести. На­блюдения показывают, что из-за инерционности частиц жидкости, подходящих к отверстию изнутри резервуара, площадь сечения струи после выхода из отверстия меньше площади отверстия. Иными словами, происходит сжатие струи. Учтем далее, что размер отверстия d₀ может влиять на скорость истечения, поскольку через него определяется число Рейнольдса, характеризующее влия­ние сил вязкости. При этом определяющими параметрами являются d₀, v, . р и μ. Два возможных -параметра

дают зависимость

2р(v ²) = f(Re)

где множитель 2 введен для получения формулы общепринятого вида.

Отсюда скорость истечения

Если под скоростью v понимать среднюю скорость струи, то ее надо отнести к сжатому сечению С — С, где струйки почти параллельны. Тогда расход

Обозначая через  коэффициент сжатия, т. е. отношение площади сжатого сечения к площади отверстия, и через  функцию f (Re), получим широко известную формулу гидравлики

Обычно величины  = 1/ называют коэффициентом скорости,  = ₀— коэффициентом расхода. Тогда окончательно