5.11. Подобие гидромеханических процессов

Несмотря на высокий уровень развития современной гидродинамической теории, далеко не все задачи могут быть решены теоретически с достаточной для практических целей точностью. Многие задачи приходится решать экспериментально. При создании современных гидравлических и газодинамических машин, приборов, летательных аппаратов, сооружений и t. п. гидродинамический расчет является важнейшим и обязательным этапом проектирования, но все же результирующая оценка качеств и характеристик создаваемой машины или сооружения производится на основе экспериментальных испытаний модели или натурного объекта. Роль гидродинамического эксперимента

Рис. 5.10. Схема для объяснения геометрического и кинематического подобия потоков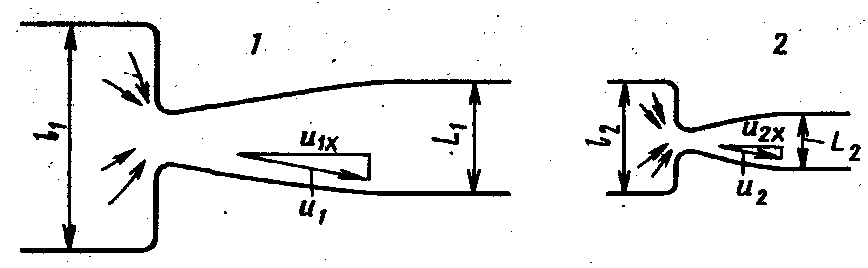

велика, и существует обширный раздел гидромеханики, составляющий в значительной степени самостоятельную дисциплину — экспериментальную гидродинамику (или экспериментальную аэродинамику, если речь идет об опытах с воздушной средой).

При постановке гидродинамического эксперимента одним из основных является вопрос о том, по каким правилам должна быть изготовлена модель испытуемого объекта и по каким зависимостям следует пересчитать данные опытов, чтобы получить достоверное описание натурного гидродинамического явления. На этот вопрос дает ответ раздел гидромеханики, называемый теорией подобия, которая по существу является теоретической основой эксперимента. Кроме того, теория подобия дает методы построения рациональной структуры теоретических зависимостей и комбинаций входящих в них параметров, чем облегчается анализ и получение обобщенных выводов из теоретических решений.

В теории подобия различают геометрическое подобие являющееся подобием границ областей течений, кинематическое подобие, под которым подразумевают подобие полей местной скорости, и динамическое подобие, являющееся подобием сил. Дадим более полное их определение.

Пусть имеется натурный объект (поток) (рис. 5.10), подлежащий гидродинамическому исследованию, и его модель. Все параметры натурного потока будем отмечать индексом 1, а модельного — индексом 2. Чтобы получить область течения, геометрически подобную натурному потоку, разделим все линейные размеры последнего на некоторое число m_l — линейный масштаб и полученные результаты примем за соответствующие линейные размеры модельного потока. Число m_l выбирают из практических соображений, которые диктуются, например, производственными возможностями лаборатории.

Таким образом, получаем связь между геометрическими параметрами l₁, и 1₂ потоков 1 и 2:

(5.84)

Линейные размеры, связанные соотношением (5.84), называют соответственными или сходственными. Точки, координаты которых удовлетворяют этому соотношению, называют сходственными.

Модельный поток 2, геометрические параметры которого удо­влетворяют условию (5.84), назовем геометрически подобным потоку 1. Иначе можно сказать, что два потока будут геометри-

чески подобными, если любой линейный размер одного из них можно получить из линейного размера другого путем умножения на постоянный множитель.

Если в потоке 1 выбрать характерный линейный размер L₁, то в потоке 2, геометрически подобном, ему будет соответствовать сходственный размер L₂, Приняв L₁ и L₂, за единицы измерения всех линейных величин в соответствующих потоках, найдем безразмерные отношения

которые, в частности, могут быть безразмерными координатами некоторых точек. Поскольку

ясно, что = Следовательно, безразмерные координаты сходственных точек одинаковы.

Допустим теперь, что потоки 1 и 2 геометрически подобны. Обозначим через u₁ и u₂ скорости в их сходственных точках, а через u_1i и u_2i, ( их одноименные проекции на i-ю ось координат. Если отношение

(5.85)

одинаково для любой пары сходственных точек, то потоки 1 и 2 будем считать кинематически подобными.

Для неустановившегося течения условие (5.85) должно выполняться в моменты времени, которые называются сходственными и определяются соотношением

где t₁и t₂ — интервалы времени, отсчитываемые от момента начала движения или иного условного начала отсчета времени; m_t— масштаб времени.

Нетрудно убедиться, что из кинематического подобия потоков вытекает геометрическое подобие их линий тока. Действительно, линии тока в потоках 1 и 2 определяются уравнениями

Если имеет место кинематическое подобие [см. формулу (5.85)], то

Это соотношение означает, что углы наклона касательных к линиям тока в сходственных точках одинаковы для обоих потоков, а это и есть геометрическое подобие линии тока. Для установившихся потоков это будет одновременно и геометрическим подобием траекторий жидких частиц.

Кинематическое подобие можно определить и несколько иначе. Если t₁и t₂ — малые интервалы времени, за которые жидкие частицы проходят сходственные отрезки путей, то

откуда масштаб времени

Если m_t = const, то и m_u == const, так как m_l== const, что соответствует определению кинематического подобия. Поэтому иногда кинематически подобными называют потоки, для которых отношение отрезков времени, затрачиваемых жидкими частицами для прохождения сходственных отрезков путей, постоянно.

Предоставляем читателю возможность самостоятельно убе­диться, что если выбрать характерные значения скоростей v₁ и v₂, то при кинематическом подобии безразмерные скорости в сходственных точках одинаковы:

Рассмотрим далее какую-либо пару сходственных точек и обозначим проекции на координатные оси равнодействующих сил через F_1i и F_2i (i = х, у, z). Если

(5.86)

есть величина постоянная для любой пары сходственных точек, то потоки 1 и 2 называют динамически подобными.

Не обязательно под F_1i и F_2i подразумевать равнодействующие; это могут быть силы какой-либо определенной физической природы (тяжести, вязкости, упругости и др.). Тогда приведенное определение будет выражать подобие данной категории сил. Можно убедиться, что безразмерные значения сил в динамически подобных потоках одинаковы. Заметим еще, что поскольку выражение (5.86) относится к любой из трех составляющих силы F, то этим определяется подобие векторов сил, действующих в сход­ственных точках.

Из изложенного следует, что кинематическое и динамическое подобия могут существовать только при наличии геометрического подобия. Поэтому дальше речь пойдет только о потоках, для которых геометрическое подобие заведомо обеспечено.

Если для какой-либо группы гидродинамических явлений имеет место кинематическое и динамическое подобие, то их называют механически подобными. Механическое подобие является частным случаем общего подобия физических процессов, которое можно определить для тепловых, электрических, упругих и других явлений.

Сформулируем условия, необходимые и достаточные для существования механического подобия, на примере изотермического течения несжимаемой вязкой жидкости.

Из определений кинематического и динамического подобий следует, что если они обеспечены, то безразмерные координаты сходственных точек, скорости и силы одинаковы. Нетрудно убедиться, что безразмерные ускорения и плотности также равны в сходственных точках. Иначе, все физические параметры механически подобных потоков, представленные в безразмерном виде для сходственных точек, одинаковы. Можно, наконец, сделать вывод, что безразмерные поля физических параметров таких потоков одинаковы. Одинаковость безразмерных значений физических параметров можно было бы принять за определение механического подобия и вывести из него первоначальную формулировку.

Физические параметры в любом из потоков связаны системой дифференциальных уравнений, описывающих движение. Но если речь идет о механически подобных потоках, для которых безразмерные параметры одинаковы, то сами уравнения, представленные в безразмерном виде, должны быть одинаковыми. Действительно, дифференциальные уравнения движения связывают между собой мгновенные значения физических параметров движения (сил, ускорений и др.). Но если безразмерные выражения этих параметров одинаковы в подобных потоках, то, поскольку связывающие их уравнения имеют общий характер, т. е. выполняются для произвольных пространственно-временных точек, эти уравнения должны быть одинаковыми.

Заметим, что для существования подобия необходимо, чтобы рассматриваемые процессы были качественно одинаковыми. Можно, например, рассмотреть движение в одном и том же канале несжимаемой жидкости и газа при сверхзвуковых скоростях. Эти течения качественно различны потому, что при движении газа существенно проявляется его сжимаемость и изменение температуры, и описывающие его уравнения будут содержать члены, которых не будет в уравнениях несжимаемой жидкости, Поэтому дифференциальные уравнения этих двух процессов различны, даже после приведения к безразмерному виду.

Наряду с этим существуют качественно различные явления, описываемые одинаковыми по форме уравнениями. Такие явления называют аналогиями.

Совокупность параметров, определяющих какой-либо гидродинамический процесс, можно рассматривать как конкретное решение дифференциальных уравнений этого процесса. Ему соответствуют вполне определенные начальные и граничные условия. Они представляют собой зависимости или константы, определяющие физические параметры в начальный момент и на границах во время движения. Следовательно, не только уравнения процесса, но также безразмерные формы начальных и граничных

условий: (условий однозначности) в механически подобных потоках должны быть одинаковыми. Имея это в виду, запишем уравнения Навье — Стокса и приведем их к безразмерному виду, для чего выберем характерные физические параметры L, V, Т, Р, F₀ (если F — сила тяжести, то в качестве F₀ удобно взять ускорение g свободного падения) и отнесем к ним соответствующие размерные величины:

Для плотности и вязкости, которые считаем постоянными, характерные величины не выбираем, так как они сами ими являются. Примем также во внимание размерность дифференциальных операторов  и grad:

Векторное уравнение Навье—Стокса (5.11) теперь можно представить в виде

Чтобы придать этому уравнению безразмерный вид, разделим все его члены на коэффициент V²/L при конвективном ускорении. Получим

(5.87)

где все дифференциальные операции выполняются по безразмерным переменным. В этом уравнении все члены, включая комбинации характерных параметров, безразмерны. Для, всех динамически подобных потоков оно должно быть одинаковым, а следовательно, необходимо, чтобы коэффициенты каждого из членов для этой группы потоков были одинаковыми, т. е.

Входящие в условия (5.88) безразмерные комплексы играют роль критериев подобия и имеют следующие собственные наименования: V²/(FoL) = Fr — число Фруда; P/(V²) = Eu—число Эйлера; VL/v = Re — число Рейнольдса; L/(VT) = Sh — число Струхала (вместо обозначения Sh иногда употребляют обозначение Н и называют его числом гомохронности).

Теперь условия (5.88) можно записать в виде

Fr =idem; Eu=idem; Re =idem; Sh = idem. (5.89)

Суммируя изложенное, можно констатировать, что одинаковые безразмерные дифференциальные уравнения, описывающие группу гидродинамических процессов, вместе с безразмерными условиями однозначности (начальными и граничными условиями), а также одинаковые значения критериев подобия являются необходимыми условиями механического подобия. Доказать их достаточность удается не во всех случаях, так как это связано с вопросом о су­ществовании и единственности решений уравнений Навье — Стокса. Рассмотрим этот вопрос подробнее.

Допустим, что для изучаемого класса течений теорема суще­ствования и единственности решений уравнений Навье — Стокса доказана. Зафиксируем конкретные значения критериев (6.89) и сформулируем в безразмерных величинах условия однознач­ности для безразмерных уравнений Навье — Стокса. Тогда решив их, получим единственное решение, в которое в качестве параметров войдут зафиксированные значения чисел Fr, Eu, Re, Sh. Это решение определит целый класс физически реальных процессов, размерные параметры которых в сходственных точках будут, отличаться только численными множителями, а безразмерные будут одинаковыми. Иначе говоря, получим класс механически подобных потоков.

Следовательно, сформулированные выше условия в данном случае оказываются не только необходимыми, но и достаточными для существования механического подобия. Однако такое заключение нельзя распространить на произвольное движение вязкой жидкости, поскольку теорема существования и единственности решения уравнений Навье — Стокса доказана хотя и для многих, но все же частных классов движения. В общем случае необходи­мые и достаточные условия подобия не определены. Правда, это не исключает возможности практического использования теории подобия. В практике при постановке эксперимента существование и единственность группы потоков, подобных натурному, пред­полагают apriori, модель выполняют, исходя из необходимых условий подобия, и ее принадлежность к указанному классу проверяют на основе сопоставления частично известных натурных данных с результатами измерений на модели.

Выясним физический смысл чисел Fr, Eu, Re, Sh и соответ­ствующих критериев (5.89). Выражения для них получены деле­нием коэффициентов при отдельных членах уравнений движения на коэффициент при конвективной силе инерции. Эти члены представляют собой отнесенные к единице массы силы различной физической природы: V²/gL == Fr характеризует отношение (ни не равно ему) силы инерции к силе тяжести; VL/v = Re — отно­шение силы инерции к силе вязкости; P/(V)² == Eu — отношений силы давления к силе инерции; L/(VT) = Sh — отношение локальной инерционной силы к конвективной. Таким образом, все критерии характеризуют отношения сил различной физической природы и потому являются критериями динамического подобия.

Рассмотрим теперь некоторые аспекты практического применения подобия гидродинамических явлений.

При постановке любой гидродинамической задачи должны быть заданы граничные, а для нестационарных задач и начальные условия в виде функциональных связей или значений констант, которым должны удовлетворять некоторые параметры процесса на граничных поверхностях (в том числе и на свободных). Параметры внутри области течения, а также не заданные на границах необходимо определить. Например, при исследовании установив­шегося движения жидкости в некотором канале заранее известно, что скорости на стенках канала равны нулю, а распределение скоростей во входном поперечном сечении может быть задано. Скорости внутри потока, а также давления внутри канала и на его стенках следует определить. Поэтому при построении модели можно произвольно выбрать линейный масштаб, а критерии подобия определить лишь те, которые составлены из заданных величин, относящихся к границам.

В рассматриваемом примере при постановке исследования можно определить число Re (по размерам входного сечения и заданной на входе скорости), но нельзя определить число Еu, так как давления заранее неизвестны. В каждой задаче некоторые из критериев можно найти лишь после ее решения, т. е. они являются функциями других критериев, которые выражаются через исход­ные данные и называются определяющими. В зависимости от постановки задачи определяющие критерии могут становиться неопределяющими и наоборот. Но может оказаться, что ни один из указанных выше критериев не является определяющим, так как в любой из них входит величина, подлежащая определению. Тогда роль определяющего критерия может выполнить комбинация этих критериев. Примеры, иллюстрирующие это положение, приведены в следующем параграфе.

Для получения полного механического подобия необходимо одновременное равенство в сравниваемых потоках нескольких критериев. Выясним совместимость критериев Fr и Re. Из условия Fг == idem получим

где индексами 1 и 2 отмечены соответственно параметры натурного и модельного потоков.

Следовательно, масштаб скоростей должен быть связан с линейным масштабом соотношением

Полагая m_g = 1, видим, что по критерию Фруда скорость модельного потока должна быть меньше скорости натурного в раз. По критерию Рейнольдса Re = idem получим

Масштабы величин связаны соотношением

откуда следует, что для одной и той же жидкости (m_v == 1) скорость модельного потока должна быть больше скорости натурного в m_l раз. Это противоречие с требованиями критерия Фруда можно было бы устранить путем выбора надлежащего масштаба вязкости m_v, что, однако, практически невозможно, так как экс­перименты можно проводить лишь с водой и воздухом и только в редких случаях использовать другие жидкости (например, масло или глицерин). Поэтому практически критерии Фруда и Рейнольдса являются несовместимыми.

Однако в каждом гидродинамическом явлении можно указать лишь одну внешнюю силу, влияние которой на характер движения является основным, определяющим и, не учитывая другие силы, моделировать по одному критерию. Практикой исследований установлено, что течения со свободной поверхностью в поле силы тяжести формируются под преимущественным влиянием этой силы и должны моделироваться по критерию Фруда.

Напорные течения, т. е. течения в закрытых трубах и каналах без образования свободной поверхности, моделируются по критерию Рейнольдса. Число Эйлера чаще всего является неопределяющим критерием и представляет собой функции Fr и Re. Конечно, моделирование по какому-нибудь одному критерию обеспечивает подобие лишь одной силы. Такое подобие является, приближенным. Однако теория подобия позволяет указать ра­циональную методику внесения экспериментальных поправок на неточность соблюдения ее требований.

Обоснование возможности не учитывать Критерий Фруда при моделировании напорных течений можно получить, если ввести вместо полного давления р разность р— p_g == р', где p_g — гидростатическое давление (р_g = р₀ + pgh, здесь р₀— постоянное давление в некоторой точке отсчета; h — заглубление, отсчитываемое вниз по вертикали от этой точки).

При вертикальном расположении оси z

После подстановки этих значений в уравнения движения последние не будут содержать членов, учитывающих массовую силу (силу тяжести), а следовательно, в числе критериев подобия будет отсутствовать и критерий Фруда. Если же поток имеет свободную поверхность, то описанный прием не дает результата. Рассмотрим для простоты открытый поток идеальной жидкости. На свободной поверхности, где р = р₀ = const, должно выполняться условие

Выбрав характерный линейный, размер L, представим это условие в безразмерном виде

Из этого соотношения следует, что форма границы области течения (свободной поверхности), определяемая безразмерной координатой z_n/L, зависит от граничного значения числа Fr_n и, следовательно, подобие не может быть осуществлено без критерия Фруда.