5.10. Общее уравнение энергии

Как следствие уравнений движения вязкой жидкости выше получено уравнение Бернулли, которое выражает теорему об изменении кинетической энергии, т. е. является уравнением баланса механической энергии. Но в природе и технике встречается множество явлений и процессов, сопровождающихся выполнением механической работы, теплообменом с внешней средой и превращением механической энергии в теплоту. В этих случаях закон сохранения энергии выражается более общим уравнением и не является следствием уравнений движения.

Для получения общей формы уравнения, выражающего закон сохранения энергии, выделим конечный объем W сжимаемой или несжимаемой жидкости, ограниченный поверхностью S и находящийся в движении. Рассматривая массу этого объема жидкости как неизолированную термодинамическую систему, можно применить к ней закон сохранения и превращения энергий, согласно которому изменение полной энергии системы равно сумме притока теплоты к системе и совершенной над ней работы внешних сил.

Для выражения каждой из упомянутых в этой формулировке величин обозначим через U внутреннюю энергию * единицы массы жидкости; q — количество теплоты, подводимое к единице массы жидкости за единицу времени; обозначения остальных величии оставим прежними.

Полная энергия Э выделенного жидкого тела складывается из внутренней и кинетической энергий и ее можно выразить интегралом

(5.76)

а изменение энергии за время dt — дифференциалом

В нешние силы могут быть поверхностными и массовыми. Работу первых можно рассчитать, выделив на поверхности S площадку dS и приняв во внимание, что сила, распределенная по ней, равна p_ndS. Если за время dt площадка dS перемещается на расстояние ds = udt, то работа этой силы будет равна скалярному произведению силы на путь: p_ndsdS, а суммарная работа поверхностных сил выразится интегралом

Работу массовых сил можно представить в виде

где ds — элементарное перемещение кассы  dW за время dt.

____________________

* Под внутренней понимают энергию, равную сумме кинетических и потенциальных энергий всех составляющих жидкое тело частиц (молекул, атомов, ионов и др.).

**Аддитивность внутренней энергии имеет место не во всех случаях, но мы ограничимся предположением, что энергию отдельных частиц можно суммировать. Следует обратить внимание на то, что здесь в полную энергию не включается потенциальная энергия положения. Это означает, что сила тяжести является внешней и ее работа учитывается в правой частя уравнения.

Полное количество теплоты, подведенное к массе жидкости в объеме W за время dt, равно

Теперь можно написать уравнение, выражающее закон сохра­нения энергии:

Разделив члены этого выражения на dt и учитывая, что ds/dt = и есть скорость движения жидких частиц, получаем интегральную форму закона сохранения энергии •

Для получения дифференциальной формы этого уравнения учтем, прежде всего, что dW = dm есть масса объема dW, остающаяся постоянной во время движения. Следовательно, dm/dt = 0 и

Далее преобразуем поверхностный интеграл правой части уравнения (5.77) в объемный. Для этого учтем выражение (3.4) напряжения р_n, и, используя известную формулу

где b_i — i-я проекция произвольного вектора; n — направление нормали к поверхности S,

получим

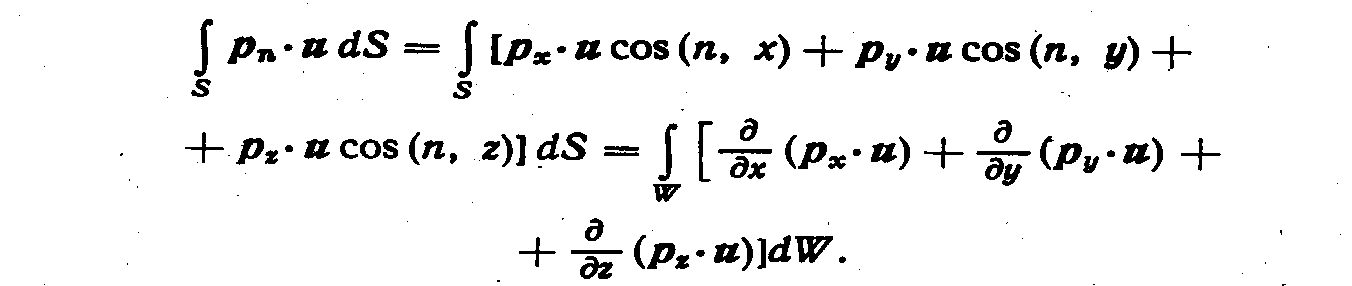
Подставляя последние два соотношения в уравнение (5.77) и отбрасывая знак интеграла ввиду произвольности объема W,

__________________

*Термин «сохранение» следует понимать как «неуничтожимость», а не как «постоянство» или «неизменность». Постоянство полной энергии имеет место только при тепловой изоляции системы и отсутствии действия внешних сил.

получаем дифференциальное уравнение энергии для произвольного движения сжимаемой вязкой жидкости:

(5.78)

Уравнения (5.77) и (5.78), выражающие в разных формах общий закон сохранения энергии, могут быть прочитаны следующим образом: производная по времени от полной энергии жидкого тела равна сумме мощностей внешних (массовых и поверхностных) сил и притока теплоты к нему за единицу времени.

Рассмотрим детально члены уравнения (5.78), выражающие мощность внешних поверхностных сил, обозначив ее N_p. Продифференцировав скалярные произведения, получим

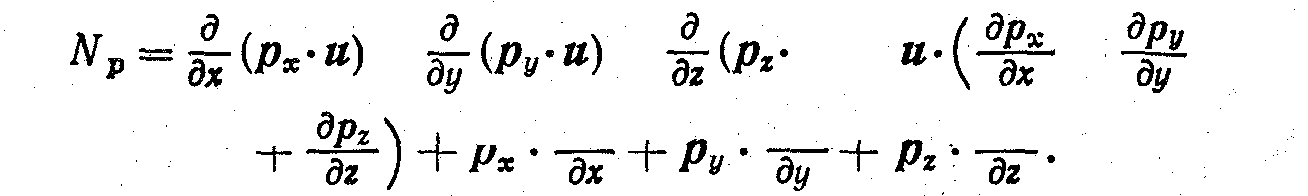
Вычислим величину

J₁ = u ( )

для несжимаемой жидкости, воспользовавшись выражениями проекций напряжений р_х, р_y, р_z, через скорости деформаций согласно формуле (5.6). Учитывая при этом, что для несжимаемой жидкости div u = 0, после преобразований получим

J₁ = -u grad p+ u²u

Для величины

J₂=

в результате аналогичных преобразований находим

J₂ =Ф_Д

где

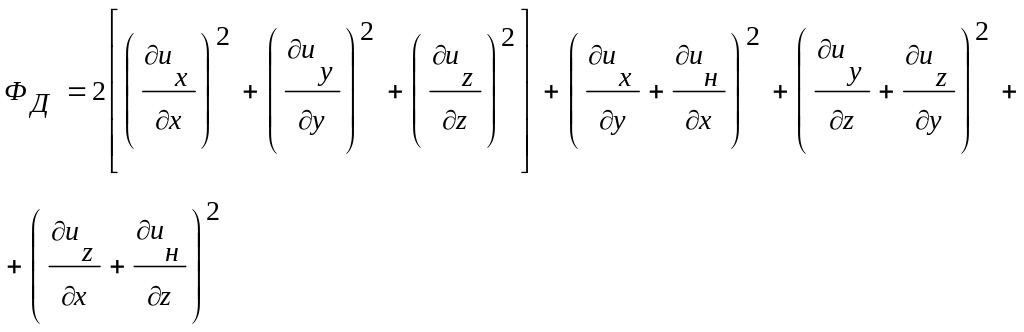
называется диссипативной функцией.

Можно показать, что величина J₂, равна мощности внутренних вязкостных напряжений, которая расходуется на преобразование механической энергии в тепловую. Поэтому функция Ф_д характеризует процесс диссипации энергии (от латинского dissipare — рассеивать).

Теперь уравнение (5.78) перепишем в виде

Если учесть, что

и использовать уравнение (5.10) Навье—Стокса, умножив его скалярно на и, то вместо выражения (5.79) получим уравнение

(5.80)

называемое уравнением притока теплоты. Если обозначить через Э_к = и²/2 кинетическую энергию единицы объема жидкости, то формулу (5.79) можно представить в виде

(5.81)

где Э =  (U + u/2)² — полная энергия единичного объема.

Полученные формы уравнения энергии позволяют описать процесс ее преобразования в движущейся вязкой жидкости. Так, формула (5.78) выражает закон сохранения энергии: изменение полной энергии среды в единицу времени равно мощности внешних массовых и поверхностных сил плюс приток теплоты за то же время. Тот же смысл имеет уравнение (5.79), в котором мощность внешних поверхностных сил выражена суммой

Из уравнения (5.80) следует, что изменение внутренней энергии за единицу времени обусловлено диссипацией механической энергии (превращением ее в тепловую) и притоком теплоты извне за то же время. Процесс диссипации зависит только от вязкости и для идеальной жидкости (= 0) не имеет места. Из уравнения (5.81) следует, что изменение полной энергии складывается из изменения кинетической энергии, тепловой энергии, полученной от диссипации и притока теплоты извне.

Если же учесть, что изменение полной энергии в единицу времени равно мощности всех внешних сил, то можно сделать вывод, что эта мощность частично расходуется на изменение кинетической энергии, а частично теряется вследствие процесса диссипации (теорема о диссипации энергии).

Вычитая из выражения (5.79) уравнение (5.80), получаем

Это уравнение выражает теорему живых сил (теорему кинетической энергии): производная по времени кинетической энергии жидкого объема равна сумме мощностей всех внешних и внутрен-

них сил, действующих на эту массу. При этом мощность всех поверхностных сил выражается суммой двух последних членов. Если учесть, что u = ds/dt, где ds — вектор элементарного перемещения, то нетрудно доказать, что выражение (5.82) совпадает с уравнением Бернулли (5.19).

Придадим общему уравнению энергии еще одну форму, дополнительно поясняющую процесс трансформации энергии в жидкой среде. Учтем, что индивидуальную производную dЭ/dt полной энергии можно представить как сумму локальной и конвективной; используем также уравнение неразрывности div u = 0. Тогда

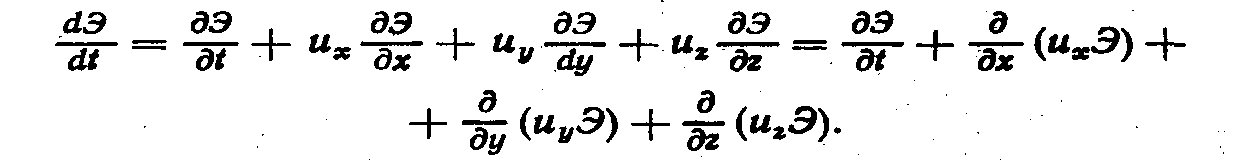
Подставляя это выражение в уравнение (5.79), получаем

Если ввести в рассмотрение вектор Е с проекциями на оси

то последнее уравнение примет вид

(5.83)

Вектор Е называют вектором плотности потока полной энергии, а уравнение (5.83)—уравнением переноса полной энергии [22]. Из него следует, что изменение в единицу времени полной энергии в точке складывается из мощности внешних массовых сил и притока энергии, который в свою очередь обусловлен конвективным переносом и работой внешних поверхностных сил.