26

2. Кинематика жидкости

_________________________________________________________________

2.1. Два метода описания движения жидкости

Кинематика жидкости является разделом гидромеханики, в котором движение изучается вне зависимости от действующих сил; в кинематике устанавливаются связи между координатами жидких частиц, их скоростями, ускорениями и другими параметрами, а также закономерности их изменения во времени.

Благодаря текучести жидкой среды отсутствуют жесткие связи между ее отдельными частицами, и общий характер движения оказывается более сложным, чем характер движения твердого тела.

Понятие скорости, одно из основных в кинематике, применительно к движению жидкости требует известной конкретизации. Так как жидкие частицы перемещаются в общем случае с разными скоростями, то употребляется термин «скорость жидкой частицы». Однако последняя представляет собой сплошную совокупность материальных точек, заполняющих некоторый малый объем, деформируемый во время движения. Поэтому приведенный термин оказывается недостаточно конкретным. Условимся под скоростью частицы понимать скорость некоторой ее точки, условно выбираемой и называемой полюсом.

В опытах наблюдать движение жидких частиц и измерять их скорости можно различными способами. Простейшим является подкрашивание частиц краской той же плотности, что и изучаемая жидкость. Наблюдения за поведением таких подкрашенных частиц показывают, что при определенных условиях, которые будут установлены в гл. 6, частицы могут двигаться упорядоченно, образуя слоистое или ламинарное течение (от лат. lamina — пластина, полоска). При других условиях частицы, наряду с основным движением по некоторому преимущественному направлению, перемещаются из слоя в слой, их мгновенные скорости резко изменяются по величине и направлению. Иными словами, в этом случае на упорядоченное движение частиц накладывается хаотическое или пульсационное движение, приводящее к разрушению слоистой структуры и перемешиванию слоев. Такое движение получило название турбулентного (от лат. turbulentus — беспорядочный). Столь сложное движение жидкости требует специфических способов его математического описания.

Одним из таких способов является определение зависимости от времени координат точки, в которой в данный момент находится наблюдаемая жидкая частица. Эту зависимость можно выразить в координатной форме

x = x (t); у = у (t); z = (t),

или в векторной

r = r (t);

где r — радиус-вектор точки с координатами х, у, z; t — время.

Но, очевидно, для описания движения конечной массы жидкости этой зависимости недостаточно, так как в ней не содержатся параметры, выделяющие данную частицу из бесконечного множества других. В качестве таких параметров можно, например, выбрать значения декартовых прямоугольных координат , ,  той точки пространства, в которой частица находилась в начальный момент времени t₀. Тогда положение любой частицы в произвольный момент времени будет определено зависимостями

х = x (t, , , ); у = у (t, , , ,); z = (t, , ,  )

или векторной функцией

r = r (t, , , , );

Имея эту зависимость, можно выразить мгновенную скорость жидкой частицы в виде вектора

u = дr/дt (2.1)

или в проекциях на оси координат

u_x = дх/дt; и_у = ду/дt; u_z = дz/дt . (2.1¹)

Ускорение и его проекции определяются формулами

а = д²r/дt²; (2.2)

а_x = д²x / дt²; а_y = д²y / дt²; а_z = д²z / дt². (2.2')

Если параметры , ,  зафиксированы, то приведенными соотношениями устанавливаются кинематические характеристики конкретной жидкой частицы, аналогично тому, как определяются соответствующие характеристики материальной точки. При изменении величин , ,  осуществляется переход от одной жидкой частицы к другой, таким образом можно охарактеризовать движение всей конечной массы жидкости. Изложенный способ описания движения жидкой среды называется методом Лагранжа *, а параметры , , — переменными Лагранжа.

__________________

* Жозеф Луи Лагранж (1736—1813) — выдающийся французский математик и механик, член Парижской академии наук. Автор фундаментальных исследований по многим разделам математики. Основоположник аналитической механики.

Несмотря на весьма полную информацию о движении массы жидкости, которую дает этот метод, он не получил преимущественного применения в гидромеханике и употребляется только для решения некоторых специальных задач. Это связано с тем, что уравнения движения, составленные на основе метода Лагранжа, сложны и трудноразрешимы.

Наиболее широкое применение в гидромеханике находит метод Эйлера *, который заключается в описании поля скоростей в пространстве, занятом движущейся жидкостью. Он основан на понятии местной скорости или скорости в точке (этим термином обозначают скорость жидкой частицы, находящейся в выбранной точке пространства в данный момент времени). В общем случае местные скорости различны в один и тот же мо­мент времени в разных точках и наряду с этим могут изменяться во времени в каждой точке. Таким образом, если и — вектор местной скорости, то в общем случае

u = u (r, t) (2.3)

или в форме проекций

u_x = u_x (х, y, z, t); и_у = и_у (х, y, z, t); u_z = u_z (х, y, z, t), (2.3')

где r — радиус-вектор точки c координатами х, у, z, называемыми переменными Эйлера.

Этими функциями характеризуется поле скоростей движущейся жидкости, т. е. совокупность значений вектора u, определенного в каждой точке пространства или его части.

Если местная скорость и явно зависит от времени, т. е. изменяется с течением последнего, то движение и соответствующее ему поле скоростей называют неустановившимися или нестационарными. Если в каждой точке пространства вектор и имеет постоянное во времени значение, то движение и поле скоростей будут установившимися или стационарными. В этом случае

u = u (r) (2.4)

или в проекциях на оси координат

u_x = u_x (х, y, z); и_у = и_у (х, y, z ); u_z = u_z (х, y, z). (2.4')

Ламинарные течения могут быть как установившимися, так и неустановившимися, но турбулентные течения, строго говоря, всегда являются неустановившимися; неупорядоченное движение

•Леонард Эйлер (1707—1783) — один из крупнейших математиков мира. Швейцарец по происхождению, он длительное время жил и работал в Петербурге (1727—1741) и с 1766 г. до конца жизни являлся действительным членом Петербургской академии наук. Помимо выдающихся математических работ Л. Эйлер опубликовал ряд основополагающих результатов по гидромеханике, в том числе дифференциальные уравнения равновесия и движения невязкой жидкости.

Рис. 2.1. Пульсации скорости в турбулентном потоке

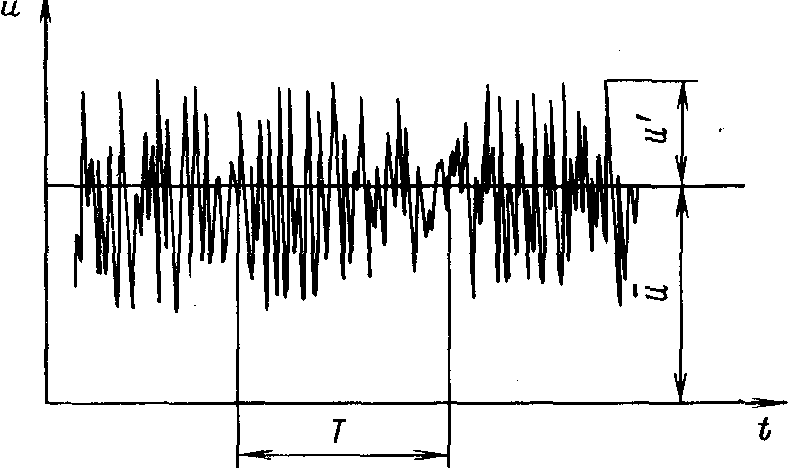
частиц в турбулентном потоке создает резкие изменения местных скоростей во времени, называемые пульсациями скорости.

На рис. 2.1 приведены результаты измерений местной мгновенной скорости турбулентного потока воздуха. Местная скорость изменяется во времени достаточно резко, однако ее значение колеблется около некоторого среднего. Поскольку использование в расчетах мгновенных скоростей приводит к трудностям и некоторой неопределенности, вводится понятие местной усредненной скорости

(2.5)

где u — мгновенная местная скорость; t— произвольный момент времени; Т — период усреднения.

Способ усреднения, выраженный соотношением (2.5), не является единственно возможным, но благодаря простоте его широко применяют в гидромеханике. При этом предполагается, что операция повторного усреднения не изменяет результата, т.е.

Проекции вектора усредненной скорости

Разность векторов u иu называют пульсационной скоростью или просто пульсацией:

u u –u;

u_x  u_x –u_x; u_y u_y –u_y; u_z  u_z –u_z;

Нетрудно убедиться, что усредненное значение пульсации равно нулю:

В случае, показанном на рис. 2.1, усредненная скорость от времени не зависит. Турбулентное течение при этом условно

называют усредненно установившимся или просто установившимся. Однако возможны случаи, когда усредненная местная скорость закономерно изменяется во времени. Такое течение называют усредненно неустановившимся. Операция усреднения для таких течений требует некоторого уточнения.

Имея в виду действительный характер движения реальных жидкостей, в дальнейшем будем считать местные скорости непрерывными дифференцируемыми функциями координат и времени, независимо от того, какое реальное течение (ламинарное или турбулентное) они описывают. Только в особых случаях будем допускать существование разрывов скоростей и их производных на некоторых поверхностях, линиях или в точках

Если функции (2.3) или (2.4) определены, то можно не только составить представление о характере движения массы жидкости, но и найти кинематические характеристики, необходимые для составления динамических уравнений движения.

Поскольку законы механики (второй закон Ньютона, закон количества движения и т. п.) сформулированы применительно к материальным телам, каковыми в механике жидкости и газа являются жидкие частицы и их конечные совокупности, то необходимо уметь, пользуясь методом Эйлера, выражать ускорения а жидких частиц. В соответствии с физическим смыслом оно определяется полной производной вектора скорости по времени:

а = du/dt.

Для выражения этого ускорения в переменных Эйлера учтем, что для движущейся частицы ее координаты являются функциями времени: х = х (t), у = у (t) и z = z (t). Тогда проекции скорости u_x, u_y , u_z будут сложными функциями времени:

u_x = u_x [х (t), у (t), z (t), t];

u_y = u_y [х (t), у (t), z (t), t]; u_z = u_z [x (t), у (f), z (f), t].

Используя правило дифференцирования сложных функций, для проекций полного ускорения получим

Поскольку для движущейся частицы dx/dt = u_x, du/dt = u_y, dz/dt = u_z, окончательно

(2.6)

Для представления ускорения

в компактной форме введем оператор Гамильтона

Рассматривая величину  формально как вектор с проекциями д/дх, д/ду и д/дz, представим первую формулу системы (2.6) в виде

Аналогично представим проекции а_.у и а_z,.

Учитывая, что выражение в круглой скобке имеет структуру скалярного произведения u  * и выражая вектор ускорения в виде а = а_x i + а_у j + а_z k, получим символическую форму полного ускорения жидкой частицы:

(2.7)

Как следует из выражения (2.7), ускорение складывается из двух частей. Первая — дu/дt, называемая локальной производной, выражает изменение во времени вектора u в фиксированной точке пространства. Эта величина определяет местное или локальное ускорение. Вторая часть — (u ) u называется конвективной производной вектора u. Эта величина выражает изменение скорости в пространстве в данный момент времени.

В частном случае установившегося движения локальное ускорение равно нулю и, следовательно,

a = (u ) u

Полная производная du/dt в формуле (2.7) называется еще индивидуальной или субстанциональной производной.