2.9. Плоские потоки несжимаемой жидкости. Функция тока и гидродинамическая сетка

Свойства течений, изложенные в предыдущих параграфах, справедливы для любых пространственных (трехмерных) течений несжимаемой или сжимаемой жидкости. Здесь же рассмотрим частный, но практически важный случай плоского течения несжимаемой жидкости, т. е. такого, в котором: а) конфигурация линий тока во всех плоскостях, нормальных некоторой прямой, одинакова и б) все линии тока являются плоскими кривыми, лежащими в этих плоскостях.

Выбрав указанную прямую в качестве одной из осей координат (например, z), заключаем, что для всего поля течения соответствующая проекция скорости равна нулю (и_z = 0).

Хотя, строго говоря, в природе плоских течений не встречается, однако существует много случаев, когда поток с достаточ­ной для целей практики точностью может считаться плоским. Например, поток воздуха, обтекающий длинное цилиндрическое крыло (рис. 2.21, а), если из рассмотрения исключить области вблизи концов крыла; поток воды в широком прямоугольном канале (рис. 2.21, б), если из рассмотрения исключить области,

Рис. 2.21. Примеры плоских течений:

а — обтекание длинного цилиндрического крыла; б – течение в широком канале

примыкающие к боковым стенкам. Подобных примеров существует множество.

Изучение плоских течений существенно облегчается, во-первых, потому, что уравнения, их описывающие, значительно проще, чем в общем случае, а во-вторых, потому, что достаточно исследовать течение всего лишь в одной плоскости, чтобы составить представление о потоке в целом.

Пусть и_z  0. Тогда уравнение неразрывности для несжимаемой жидкости имеет вид

ди_x/дx +д u_y /дy = 0 или ди_x/дx = –дu_y /дy,

(2.52)

а уравнение линий тока

(2.53)

Соотношение (2.52) является условием необходимым и достаточным, чтобы левая часть выражения (2.53) была полным дифференциалом некоторой функции двух переменных. Обозначим эту функцию через  и назовем функцией тока. Тогда

Сравнивая коэффициенты при dx и dy, получаем

и_x = д/дy;. и_y = –д/д. (2.54)

Вдоль любой линии тока выполняется условие (2.53) и, значит, вдоль нее д = 0 или  = const., т. е. функция  сохраняет вдоль любой линии тока постоянное значение, которое, однако, различно для разных линий тока.

Чтобы выяснить физический смысл функции , проведем две произвольные линии тока PQ и MN (рис. 2.22) и вычислим расход q жидкости, протекающей между ними, считая размер потока

в направлении нормали к плоскости чертежа равным единице. Используя общее выражение расхода (2.9), получаем

где l — произвольная кривая, соединяющая линии тока.

Иначе,

Как видно из рис. 2.22, dl cos (n, x) = dy; dl cos (n, y) = —dx. Тогда

т. е. разность значений функции тока на двух линиях тока равна расходу жидкости между ними. Если _А = 0, то q = _В и по­этому можно сказать, что  является расходной функцией.

Подчеркнем, что существование функции тока не зависит от наличия или отсутствия в жидкости вихрей; оно вытекает из уравнения (2.53) неразрывности для плоских течений и потому функция тока приведенного вида существует только для плоских течений. Если течение не плоское, а двумерное, т. е. одна из про­екций скорости в какой-либо системе координат равна нулю, то функция тока также существует, однако связана с проекциями скорости соотношениями, отличными от (2.54) (см. п. 7.14).

Допустим, что поток не только плоский, но и потенциальный. Тогда в нем можно провести эквипотенциальные поверхности, которые в данном случае являются цилиндрическими и в пересечении с плоскостью течения дают плоские эквипотенциальные линии. Таким образом, плоский потенциальный поток несжимаемой жидкости характеризуется двумя ортогональными семействами кривых:  = const (линии тока) и  = const (эквипотен-

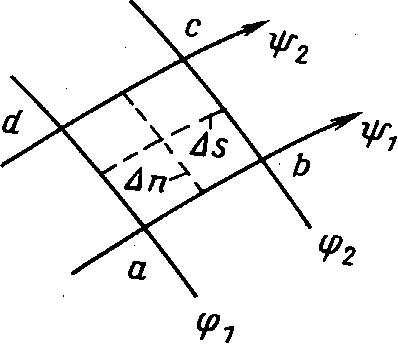
Рис. 2.22. Схема для объяснения фи­зического смысла функции тока

Рис. 2.23. К обоснованию квадратичности гидродинамической сетки

Рис. 2.24. Гидродинамическая сетка плоского потока

циали). Эти два семейства образуют гидродинамическую сетку, имеющую следующие, свойства:

1) сетка ортогональна (доказательство вытекает из содержания п. 7.2);

2) одноименные линии сетки не пересекаются нигде, кроме точек с нулевой и бесконечной скоростью (критические или особые точки); для линий тока это уже доказано (п. 2.2), для эквипотенциалей это справедливо в силу ортогональности их линиям тока;

3) сетка в малом квадратична.

Рассмотрим малую ячейку abcd (рис. 2.23), образованную парой отрезков линий тока (ab и dc) и парой эквипотенциалей (ad и bс). Пусть n — отрезок средней эквипотенциали, a  — отрезок средней линии тока. Расход через ячейку можно выразить в виде

q = u n = ,

где  –приращение функции тока на отрезке s между линиями тока аb и dc.

Но

u =  /s  /s,

где — приращение потенциала на отрезке s между эквипотенциалями ad и bс.

Тогда

q =  = (/s) n или  s = /n

Следовательно, если сетка состоит из малых криволинейных квадратов (s  n), то    и наоборот. В этом смысле употреблен термин «квадратичность».

Перечисленные свойства гидродинамической сетки позволяют использовать ее для определения параметров (в первую очередь, скоростей) плоских потенциальных потоков.

На рис. 2.24 показана гидродинамическая сетка, построенная для случая истечения жидкости под давлением из сосуда с плоскими стенками.