5.6. Модель идеальной жидкости. Уравнения движения л. Эйлера

Идеальная или невязкая жидкость является упрощенной моделью реальной (вязкой) жидкости. По предположению, идеальная жидкость имеет все свойства реальной, кроме вязкости, поэтому для получения уравнения ее движения можно применить уравнения Навье — Стокса, положив  = 0**. Тогда уравнения движения вязкого газа (5.8) и движения вязкой несжимаемой жидкости (5.9) упрощаются и принимают вид

(5.37)

Выражение (5.37) называют уравнениями Эйлера. Они описывают движение сжимаемой и несжимаемой идеальной жидкости. Их векторные формы легко получить из соответствующих уравнений Навье — Стокса, положив в них  = 0. Так, из формул (5.10)—(5.12) находим

(5.38)

т. е.

(5.39)

и

(5.40)

Удобную для интегрирования форму уравнения для сжимаемой жидкости можно получить, предположив баротропность

__________________

* Колмогоров Андрей Николаевич (род. 1903) — академик, выдающийся советский математик. Автор фундаментальных исследований по теории вероятностей, теории функций, топологии, математической логике. Выдвинул ряд плодотворных идей в статистической теории турбулентности.

** Отсюда не следует, что всякое решение уравнений Навье — Стокса будет давать соответствующее решение уравнений идеальной жидкости, если в нем положить  = 0. Дело в том, что в решении дифференциальных уравнений входят граничные условия, которые существенно различны для вязкой и идеальной жидкостей.

процесса (см. п. 4.1) и введя функцию давления, определяемую выражениями (4.5)—(4.7). Тогда уравнение (6.40) примет вид

(5.41)

Для несжимаемой жидкости

(5.42)

Используя обозначение

запишем уравнение (5.41) в компактной векторной форме

(5.43)

или в проекциях на оси координат

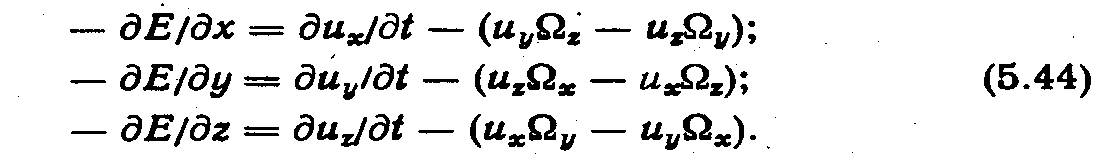
Уравнения Эйлера для несжимаемой жидкости вместе с уравнением неразрывности образуют замкнутую систему. Для сжимаемого газа эту систему необходимо дополнить по меньшей мере еще одним уравнением, например, выражающим условие баротропности или другое термодинамическое соотношение.

Граничные условия на твердых поверхностях для идеальной и вязкой жидкостей существенно различны. При движении идеальной жидкости отсутствует прилипание частиц к твердым поверхностям и жидкость скользит вдоль стенки. Граничным условием в этом случае служит непроницаемость границы, что для неподвижной стенки означает равенство нулю на ней нормальной составляющей скорости жидкости

Это условие означает, что вектор скорости касателен к граничной поверхности, т. е. последняя является линией тока. Поэтому любую линию тока в идеальной жидкости можно принять за твердую границу, не нарушив структуры течения.

Если движение идеальной жидкости потенциальное, то условию (5.45) можно придать вид

u_n_с = _с = 0,

где — потенциал скорости.

В случае плоского течения, для которого существует функция тока (х, у), граничное условие на твердой поверхности можно записать в виде

откуда следует, что твердая стенка является одной из линий тока, значение функции тока на которой равно ₀.

Если граничная поверхность задана уравнением S (х, у, z) = 0, то grad S есть вектор, нормальный к этой поверхности. Значит, условие (5.45) равносильно условию ортогональности вектора скорости на стенке u|_с и вектора grad S. Следовательно, скалярное произведение этих векторов на стенке равно нулю:

(5.47)

Для подвижной твердой границы используется условие безотрывности течения и непроницаемости стенки, которое сводится к равенству нормальных составляющих скоростей u|_с жидкости и v_n стенки:

Если подвижная граничная поверхность задана уравнением S (х, у, z, t) = 0, то последнему условию можно придать иную форму. При безотрывном движении частицы ее координаты х (t), у (t), z (t) должны в любой момент удовлетворять уравнению граничной поверхности, т. е. S [x (t), у (t), z (t), t] = 0. Так как dS = 0.

(5.49)

и, учитывая, что dx/dt = u_x, dy/dt = и_у, dz/dt = u_z, получим граничное условие на подвижной стенке

(5.50)

Граничное условие на свободной поверхности для идеальной жидкости, как и для вязкой, имеет вид