§2. Ортогональные операторы

В комплексных унитарных пространствах рассматривались унитарные операторы, т.е. операторы, сохраняющие скалярное произведение ((Ux, Uy) = (x, y)), их аналогом в евклидовых пространствах являются ортогональные операторы.

Def: Линейный оператор P, действующий в евклидовом пространстве называется ортогональным, если x, yV: (Px, Py) = (x, y).

Непосредственно из определения следует, что если {e_k} ортогональный базис в V, то {Pe_k} тоже ортогональный базис в V.

Т°. Чтобы линейный оператор P был ортогональным необходимо и достаточно,

чтобы существовал оператор P^–1 и выполнялось равенство P^* = P^–1.

◀ Необходимость. Пусть P – ортогональный.

(P^*Px, y) = (Px, Py) = (x, y)  ((P^*P – Е)x, y) = 0  P^*P = Е  (Px, Py) = (x, y)  P^* = P^–1.

Достаточность. Пусть P^* = P^–1, (x, y) = (x, P^–1Py) = (x, P^*Py) = (Px, Py) ▶

Def: Матрица называется ортогональной, если P^TP = PP^T = E.

Если е₁, е₂, …, е_n ортонормированный базис в V, то оператор P будет ортогональным тогда и только тогда когда матрица оператора будет ортогональной.

В унитарном пространстве аналогом ортогональной матрицы является унитарная матрица, т.е. такая матрица U, что U^*U = UU^* = E. Здесь U^* эрмитово сопряженная матрица, т. е. . Нетрудно показать, что в ортонормированном базисе матрица линейного оператора U унитарна тогда и только тогда, когда оператор U унитарен.

Рассмотрим ортогональное преобразование в одномерном случае хV₁, x = e, R, тогда Pe = e  (Pe, Pe) = (e, e) = ² (e, e) = (e, e), т.е. ² = 1,  = 1, таким образом, в одномерном пространстве существует два ортогональных преобразования P₊x = x и P_–x = – x.

Рассмотрим ортогональное преобразование в двумерном случае. Если P задается матрицей , то из условия P^TP = PP^T = E следует, что

т.е. . Положив a = cos, b = – sin, получим , причем во второй строке надо брать либо оба минуса, либо оба плюса. При этом detP_ = 1.

Ортогональная матрица P₊ называется собственной, а P_ называется несобственной.

В ортонормированном базисе {e₁, e₂} оператор P₊ осуществляет поворот на угол φ в плоскости {e₁, e₂}. Записав P_ = QP₊, где , можем сказать, что P_ осуществляет поворот на угол φ в плоскости {e₁, e₂} (P₊), а затем отражение относительно оси e₁ (Q).

В общем случае в n-мерном евклидовом пространстве произвольный ортогональный оператор P в некотором ортонормированном базисе {е₁, е₂, …, е_n} может быть записан в виде:

.

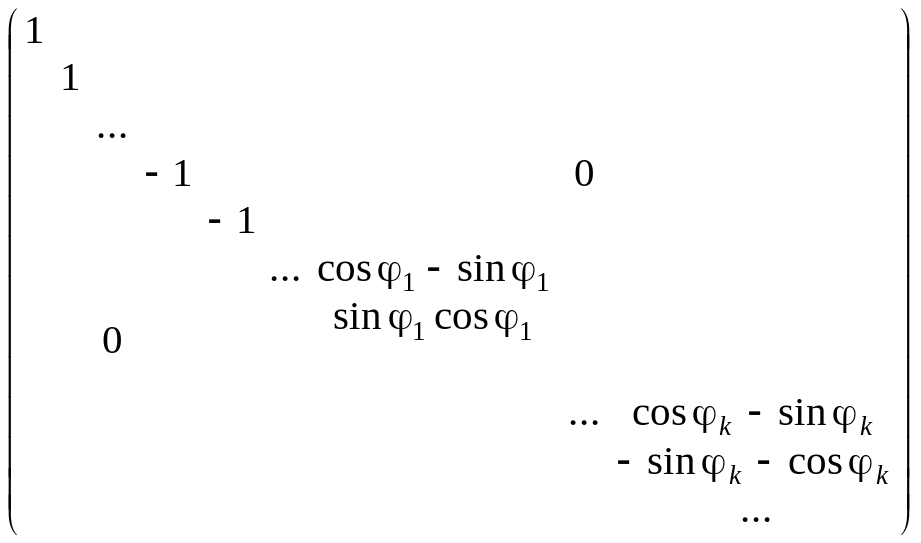Таким образом, в некотором ортонормированном базисе действие ортогонального оператора сводится к последовательным поворотам и отражениям относительно координатных осей.

Билинейные и квадратичные формы

в евклидовом пространстве

§1. Приведение квадратичной формы к сумме квадратов

в ортогональном базисе

Т°. Пусть B(x, y) – симметричная билинейная форма в евклидовом пространстве V.

Тогда существует ортонормированный базис {e_k} пространства V и существуют

_kR такие, что в указанном базисе квадратичная форма .

◀ B(x, y) – симметричная билинейная форма  A – самосопряженный такой, что B(x, y) = (Ax, y) для A {e_k} ортонормированный собственный базис  xV, ;  B(x, x) = A(x, x) = =

= ▶