§4. Понятие тензора

Пусть V – вещественное (не обязательно евклидово) линейное пространство (dimV = n).

Def: Тензором типа (p, q) , (p раз ковариантным, q раз контравариантным) называется геометрический объект, который:

1. в любом базисе {e_i} линейного пространства V_n определяется n^p+q координатами 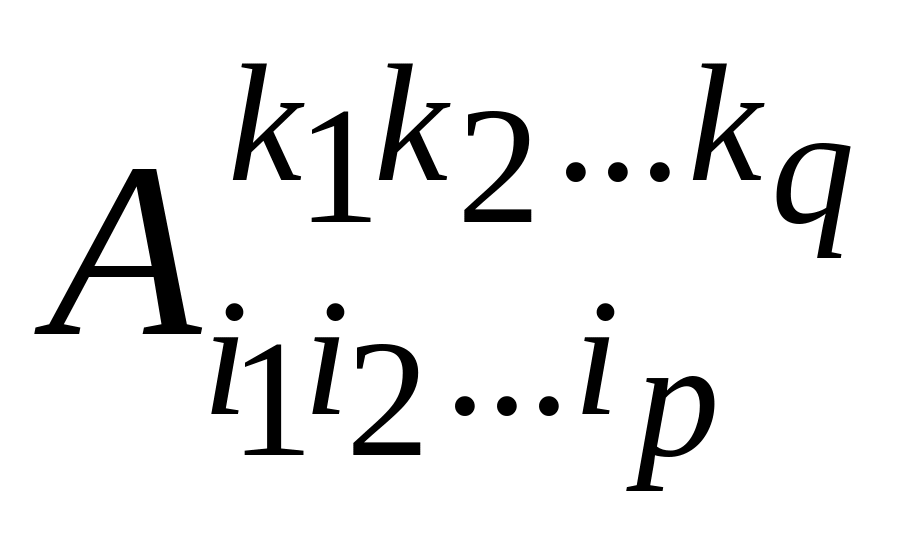(индексы принимают значения 1, 2, …, n каждый);

2. обладает свойством, что его координаты 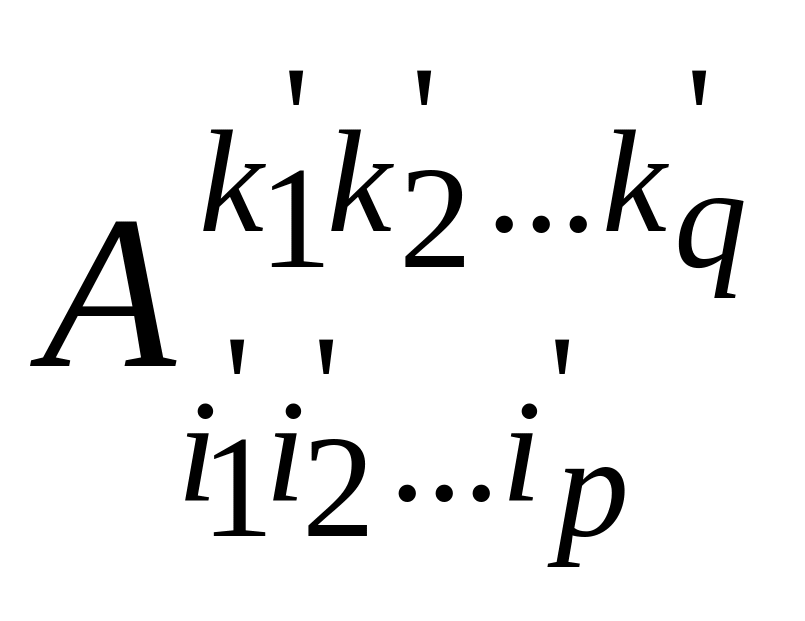в базисе {e_i} связаны с координатами в базисе {e_i} соотношениями:

; (*)

и здесь элементы матрицы перехода от старого базиса к новому (e_i  e_i), а – элементы матрицы обратного перехода.

Число r = p + q называется рангом тензора.

Формула (*) называется формулой преобразования тензора при изменении базиса.

Замечание: Индексы i₁i₂ … i_p называются ковариантными, а k₁k₂ … k_q – контравариантными.

Отметим: Ковариантные и контравариантные координаты вектора преобразуется по формуле (*) (p = 1, q = 0 для ковариантных координат, p = 0, q = 1 для контравариантных координат).

Поэтому вектор представляет собой тензор первого ранга (1 раз ковариантный, либо 1 раз контравариантный – в зависимости от выбора типа координат этого вектора).

Отметим: Скаляр – тензор нулевого ранга – имеет одну координату, причем не имеющую индексов и не изменяющуюся при изменении системы координат.

Замечание: Нетрудно убедиться в том, что последовательный переход от {e_i} к {e_i}, а затем от {e_i} к { }, приводит к тем же результатам, что непосредственный переход от {e_i} к { } , т.е. определение тензора корректно.

Замечание: Любая система n^p+q чисел может в данном базисе рассматриваться как координаты некоторого тензора А типа (p, q).

§5. Примеры тензоров

1. Нуль-тензор – это тензор все координаты которого, в некотором (а, следовательно, в

любом базисе) равны нулю.

2. Символ Кронекера. Тензор А типа (1, 1) в базисе {e_i} имеет координаты .

 = =

Т.е. действительно можно рассматривать как тензор типа (1, 1).

3. Пусть А(x, y) – билинейная форма. Напомним, что в базисе {e_i}: A(x, y) = A(xⁱe_i, y^je_j) =

= A(e_i, e_j)xⁱy^j = a_ijxⁱy^j. Здесь a_ij – элементы матрицы билинейной формы А в базисе {e_i}.

Рассмотрим, как изменяется матрица билинейной формы при переходе к базису {e_i}.

a_ij = A(e_i, e_j) = = A(e_i, e_j) = a_ij.

Равенство a_ij = a_ij, показывает, что матрица билинейной формы представляет собой тензор А типа (2, 0) ранга 2.

Пусть А линейный оператор: y=Ax. В некотором базисе : =А( )= А =

Т.е. = , – элементы матрицы линейного оператора в базисе {e_i}.

Рассмотрим базис { }.

= . Воспользуемся тем, что = ; = .

= | умножим обе части на и просуммируем по j.

=  =( )  = .

Тогда =

Последнее равенство показывает, что матрица линейного оператора может рассматриваться как тензор А типа (1,1) ранга 2.