§8. Операции над аффинными ортогональными тензорами
Отношение равенства тензоров, операции сложения, вычитания и умножения тензоров на число определяются как операции покоординатного равенства, сложения, вычитания и умножения на число в некотором базисе. Умножение и свёртка тензоров производится, как и в случае тензоров общего вида, но при свёртке отмечается не один верхний и один нижний индексы а, естественно, два нижних.
Свёртка
тензора
по индексам
и
это фактически умножение на тензор
(Здесь
тензор Кронекера).
Скалярное
произведение тензоров. Часто в
тензорной алгебре применяется комбинация
операций умножения тензоров с последующей
свёрткой по паре индексов. При этом ранг
результирующего тензора будет равен
(
),
где
-
ранги перемножаемых тензоров.
В частности
для тензоров первого ранга (векторов)
и
получаем:
=
=
+
+
,
а это просто скалярное произведение
двух векторов.
По аналогии с этим простейшим случаем, комбинацию перемножения тензоров с последующей свёрткой называют скалярным или внутренним произведением тензоров.
§9 Признак тензорности величины
Согласно определению, тензорный характер величины устанавливается по тому, как она преобразовывается при линейном ортогональном преобразовании координат.
Существует, однако, еще один способ установления тензорного характера величины. Проиллюстрируем этот способ на следующем примере:
Пусть
и
компоненты двух произвольных векторов.
Если с помощью
чисел
можно образовать скаляр
по правилу
,
то
чисел
образуют тензор 2-го ранга. Действительно:
Вычитаем из левой части равенства правую:
Отсюда, в силу произвольности векторов и :
Т.е. числа действительно являются компонентами тензора второго ранга.
Аналогично формулируется и доказывается признак тензорности для тензора любого ранга.
Пользуясь признаком тензорности, легко
проверить, что совокупность
чисел образующих символ Кронекера
является тензором 2-го ранга.
Действительно, возьмем произвольные
векторы
и
и образуем выражение
:
- скаляр.
Следовательно,
тензор 2-го ранга. Он называется единичным
тензором. Этот тензор обладает интересным
свойством: он инвариантен относительно
преобразования координат.
В самом деле:
- в силу ортогональности матрицы P.
§10 Еще раз о свойствах симметрии тензоров
Def: Если
,
то тензор
называется симметричным по индексам
и
.
Если
,
то тензор
называется антисимметричным (или
кососимметричным ) по индексам
и
.
1º Симметрия и антисимметрия тензоров инвариантна относительно преобразования системы координат.
◀ (На примере тензора ранга 2)
- симметричность
- антисимметричность. ▶
В пространстве
(размерности 3) антисимметричный и
симметричный тензоры 2-го ранга имеют
вид:
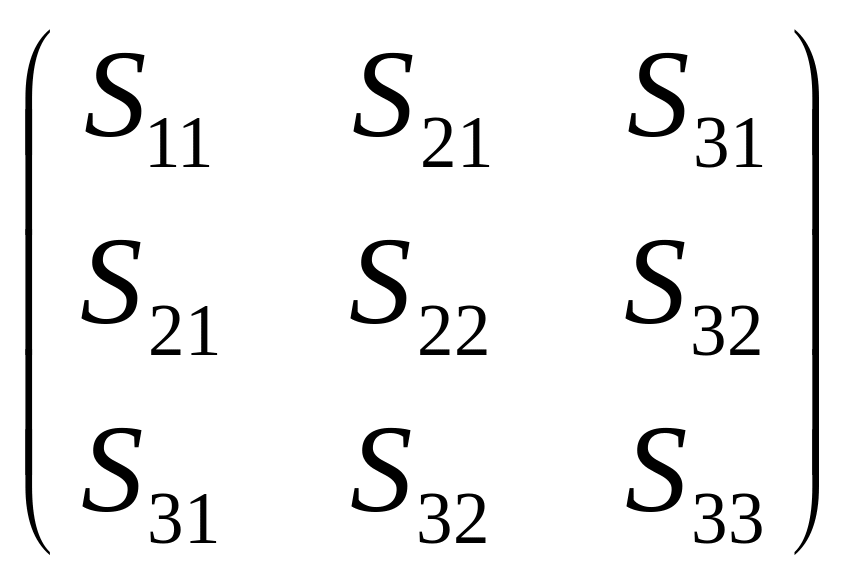и
, т.е. симметричный тензор имеет только
шесть независимых переменных, а
антисимметричный и вовсе три независимых
переменных.
Это дает возможность предложить следующую геометрическую интерпретацию симметричного и антисимметричного тензоров 2-го ранга в пространстве размерности 3:
2º. Каждому антисимметричному тензору 2-го ранга может быть поставлен в соответствие вектор и наоборот, каждый вектор связан с некоторым антисимметричным тензором 2-го ранга.
3º Любому не нулевому симметричному
тензору 2-го ранга соответствует
некоторая, и притом, единственная
поверхность второго порядка определяемая
уравнением:
(
).
4º Произведение симметрического
и антисимметрического
тензоров 2-го ранга с последующим
двукратным свертыванием равно 0.
◀ Действительно :
,
Из симметрии
:
,
индексы
и
немые, поэтому
обозначим
,
а
обозначим
:
Из антисимметрии
:
,
Т.е.
.
▶
5º Любой тензор второго ранга может
быть представлен в виде суммы симметричного
и антисимметричного тензоров, т.е.
- тензора 2-го ранга
◀
.
▶