§16. Примеры представлений групп

Р

*	I	P
I	I	P
P	P	I

ассмотрим группу G – группу симметрий трехмерного пространства, состоящего из трех элементов: I – тождественное преобразование и Р – отражение пространства относительно начала координат.

Т.е. G = {I, P}. При этом умножение элементов задано таблицей:

1) Одномерное представление группы G.

Пусть Е¹ – пространство представлений и е₁ – базис. Пусть линейный невырожденный оператор А⁽¹⁾ в этом базисе имеет матрицу А⁽¹⁾ = (1). Очевидно, это преобразование образует подгруппу в группе GL(1) причем умножение в этой подгруппе задается по правилу:

М

*	А(1)
А(1)	А(1)

ы получили одномерное представление D⁽¹⁾(G) группы G

D⁽¹⁾(I) = А⁽¹⁾; D⁽¹⁾(P) = А⁽¹⁾;

2

	A(2)	B(2)
A(2)	A(2)	B(2)
B(2)	B(2)	A(2)

) Двумерное представление группы G. Выберем в Е² базис {е₁, е₂} и рассмотрим в этом базисе матрицы преобразований: операции задаются таблицей:

Получим двумерное представление группы G с помощью соотношений: D⁽²⁾(I) = А⁽²⁾; D⁽²⁾(P)= В⁽²⁾;

Этими соотношениями определяется изоморфизм группы G на подгруппу {A⁽²⁾; B⁽²⁾} группы GL(2), т.е. это точное представление группы G.

1. Трехмерное представление группы G. Рассмотрим в Е³ в базисе {е₁, е₂, е₃} линейное преобразование А⁽³⁾ с матрицей А⁽³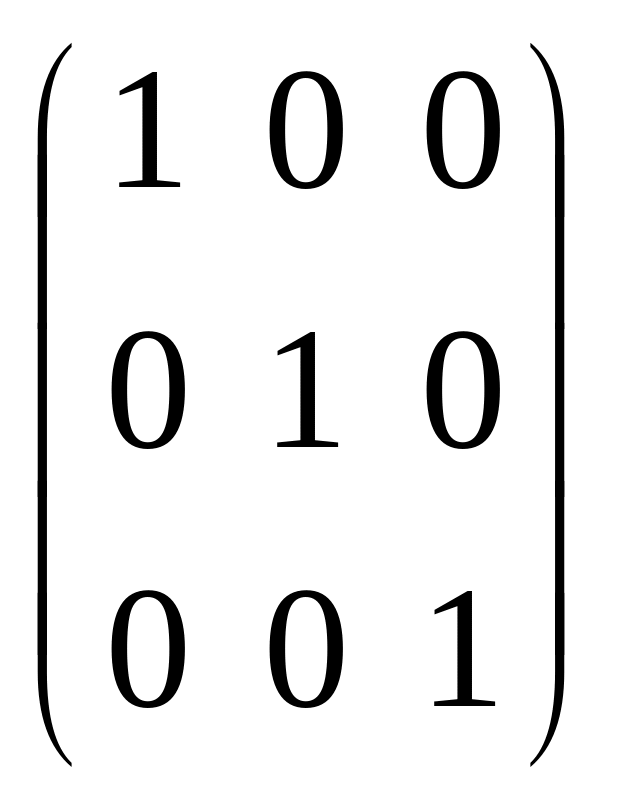⁾ = и законом умножения: А⁽³⁾А⁽³⁾ = А⁽³⁾. Получаем трехмерное представление D⁽³⁾(G) с помощью соотношений:

D ⁽³⁾(I) = А⁽³⁾; D⁽³⁾(P) = А⁽³⁾.

4) Четырехмерное представление группы G. Рассмотрим в Е⁴ линейные преобразования А⁽⁴⁾ и В⁽⁴⁾ с матрицами: 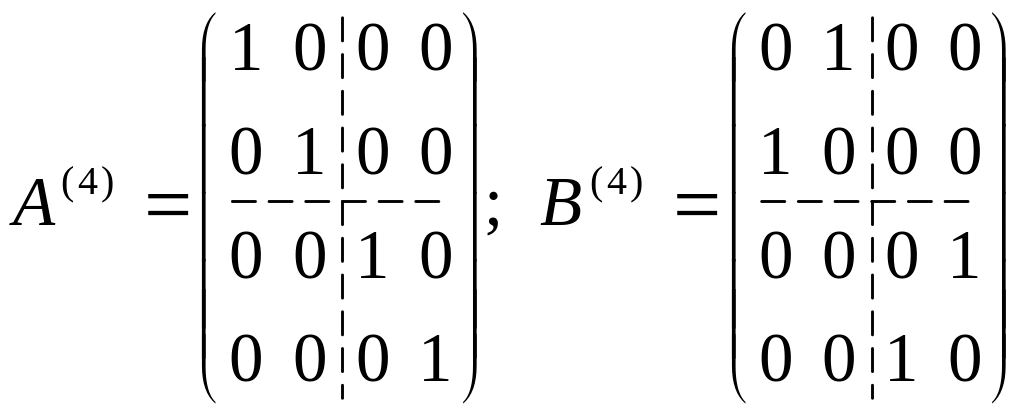. Преобразования А⁽⁴⁾ и В⁽⁴⁾ образуют подгруппу в GL(4) с законом умножения, аналогичным примеру 2, соотношениями: D⁽⁴⁾(I) = А⁽⁴⁾, D⁽⁴⁾(P) = В⁽⁴⁾.

Заметив, что А⁽⁴⁾ и В⁽⁴⁾ можно записать в виде ,

можно записать (условно): D⁽⁴⁾(G) = D⁽²⁾(G) + D⁽²⁾(G) = 2D⁽²⁾(G).

Аналогично можно условно записать D⁽³⁾(G) = 3D⁽³⁾(G).

Используя это замечание можно без труда построить представление группы G любой конечной размерности.

Элементы теории тензоров

§1. Определитель Грамма

Def: Определителем Грамма, системы векторов {e₁, e₂, …, e_k} называется определитель

Г(e₁, e₂, …, e_k) = .

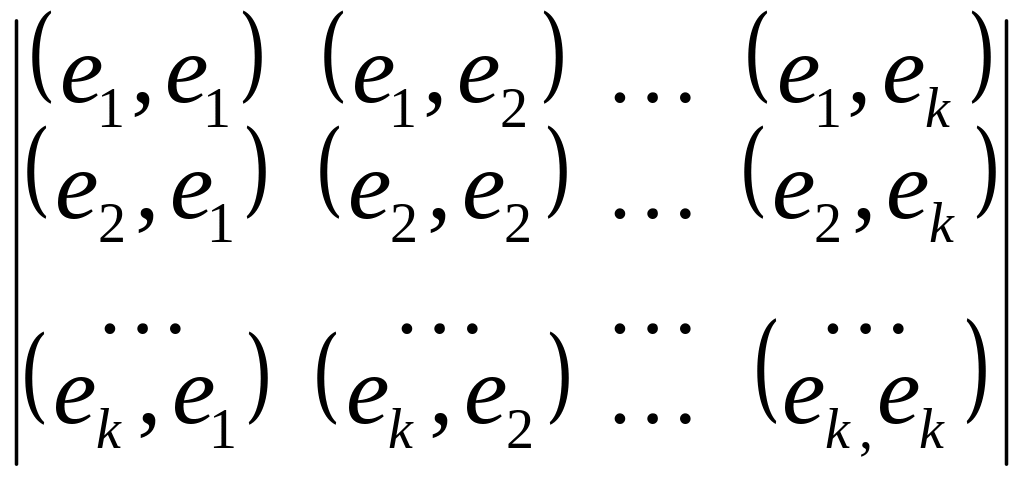Т. Для того чтобы система векторов {e₁, e₂, …, e_k} евклидова пространства E_n была

линейно-зависимой необходимо и достаточно чтобы Г(e₁, e₂, …, e_k) был равен

нулю.

◀ Необходимость. Пусть e₁, e₂, …, e_k линейно зависимы. Тогда e_k = ₁e₁ + ₂e₂ +…+ e_k–1_k–1 и в Г(e₁, e₂, …, e_k) элементы последней строки имеют вид ₁(e₁,e_i) + ₂(e₂,e_i) + …+ _k–1(e_k–1,e_i), т.е. последняя строка есть линейная комбинация остальных  Г(e₁, e₂, …, e_k) = 0.

Достаточность. Пусть Г(e₁, e₂, …, e_k) = 0  строки его линейно зависимы  ₁, ₂, …, _k ₁(e₁,e_i) + … + _k(e_k,e_i) = 0  (₁e₁ + … + _ke_k = 0 и не все _i = 0  e₁, e₂, …, e_k линейно зависимы. Противоречие ▶

Следствие. Если e₁, e₂, …, e_k линейно независимы, то Г(e₁, e₂, …, e_k)  0. Более того, Г(e₁, e₂, …, e_k) > 0

◀ Рассматриваем ℒ(e₁, e₂, …, e_k). Тогда (e_k,e_i) – элементы матрицы некоторой симметрической билинейной формы, соответствующая которой квадратичная форма определяет скалярное произведение, т.е. является положительно определенной. Следовательно, по критерию Сильвестра ₁ > 0, ₂ > 0, …, _k > 0. Но _k = Г(e₁, e₂, …, e_k) ▶