§2. Одновременное приведение пары квадратичных форм к сумме квадратов

Т°. Пусть A(x, y) и B(x, y) – симметричные билинейные формы в вещественном

линейном пространстве V. Пусть, кроме того, xV, x  0, B(x, x) > 0, т.е.

квадратичная форма B(x, x) положительно определена. Тогда в V существует

базис {e_k}, в котором: .

◀ Рассмотрим билинейную форму B(x, y) полярную к квадратичной форме B(x, x). Учитывая свойства B(x, x) в посылке теоремы, форма B(x, y), может задавать скалярное произведение в V (x, y)  B(x, y), теперь V стало евклидовым пространством {e_k} – ортонормированный базис, в котором , при этом в ортонормированном базисе ▶

Две последние теоремы дают доказательство существования и способ построения канонического базиса квадратичной формы.

Этот способ не более сложен чем, скажем, методы Лагранжа или Якоби, рассмотренные ранее. Однако доказательство полезно тем, что иллюстрирует применение самосопряженных операторов и выглядит здесь достаточно мощно.

§3. Экстремальные свойства квадратичной формы

Рассмотрим произвольную дифференцируемую функцию f на некоторой гладкой поверхности S. Точка х₀S называется стационарной (критической) точкой, если в x₀ производная f по любому направлению на поверхности S равна нулю.

Мы исследуем вопрос о стационарных (в частности экстремальных) точках и значениях квадратичной формы B(x, x) на сфере единичного радиуса в евклидовом пространстве V и о связи этих значений с собственными векторами и значениями самосопряженного оператора А, такого, что (Ax, y) = B(x, y). При этом единичной сферой в V назовем множество хV для которых (x, x) = ||x|| = 1.

Итак: пусть B(x, x) – квадратичная форма, B(x, y) – полярная ей симметричная билинейная форма, A – самосопряженный оператор: B(x, y) = (Ax, y), тогда в базисе из собственных векторов оператора А : здесь λ_k – собственные значения А.

Договоримся, что ₁  ₂  ₃  ₄  …  _n . Заметим, что в выбранном базисе уравнение единичной сферы таково: .

Т°. Стационарные значения квадратичной формы B(x, x) на единичной сфере равны

собственным значениям λ_k оператора А. Эти стационарные значения достигаются на единичных собственных векторах е_k оператора А.

Задача: найти точки экстремума B(x, x) при условии (x, x) = 1. Этo задача на условный экстремум.

◀ Можно воспользоваться методом неопределенных множителей Лагранжа.

Функция Лагранжа: . Необходимое условие экстремума: и , k = 1, 2, …, n.

Здесь _k – неопределенные множители Лагранжа.

Решение этой системы: т.е. эти решения – собственные значения и собственные векторы оператора А.

Примечание: Числа λ₁ и λ_n являются собственно наибольшим и наименьшим значением B(x, x) на сфере (x, x) = 1, т.е. , .

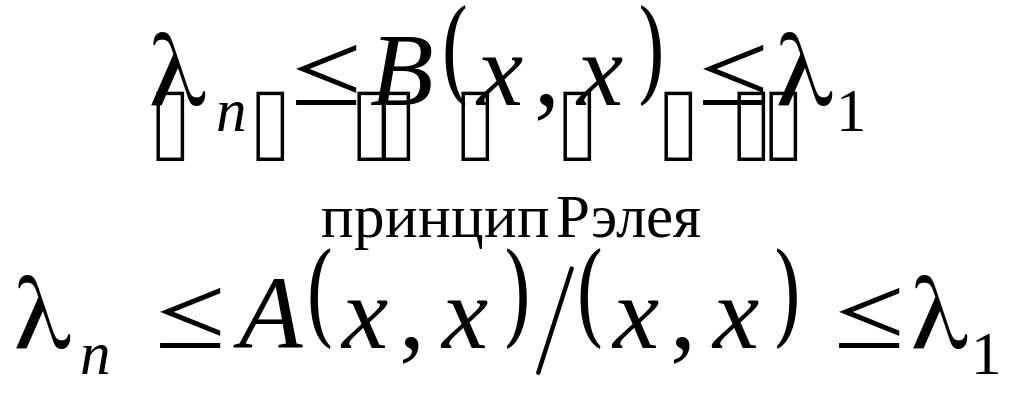Неравенства характеризуют, так называемый, принцип Рэлея. При этом, ,

Для нахождения наибольшего по модулю собственного значения оператора А, можно применить следующую процедуру: . ; ; .

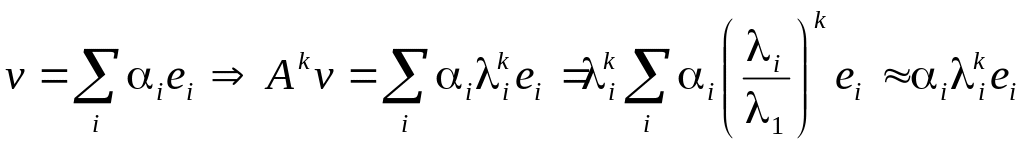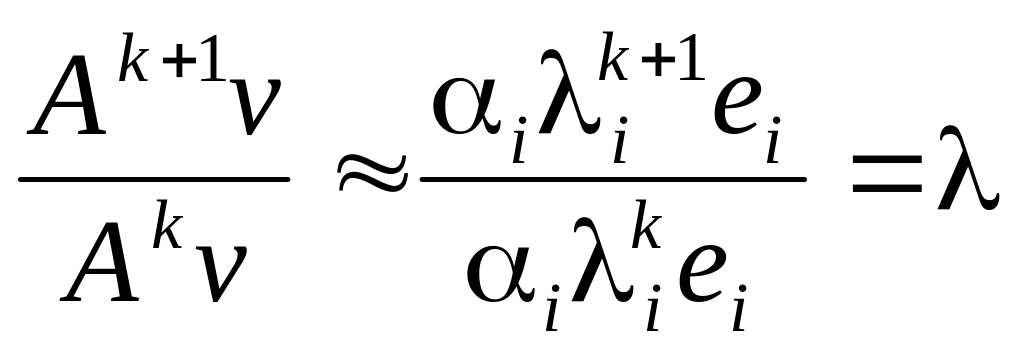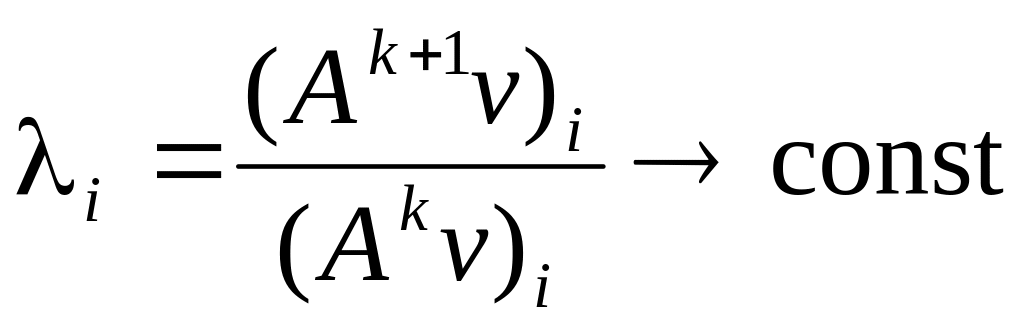Элементы теории групп §1. Понятие группы. Подгруппы

Множество G элементов x, y, z, … произвольной природы называется группой, если в нем корректно введена внутренняя операция (закон композиции) т.е. х, yG, zG такое, что z = x⊕y или (z = x⊙y), удовлетворяющее условиям:

1) x⊕(y⊕z) = (x⊕y)⊕z ассоциативность 1) x⊙(y⊙z) = (x⊙y)⊙z;

2) GxG x⊕ = x нейтральный элемент 2) еGxG x⊙е = x;

3) обратный элемент 3) .

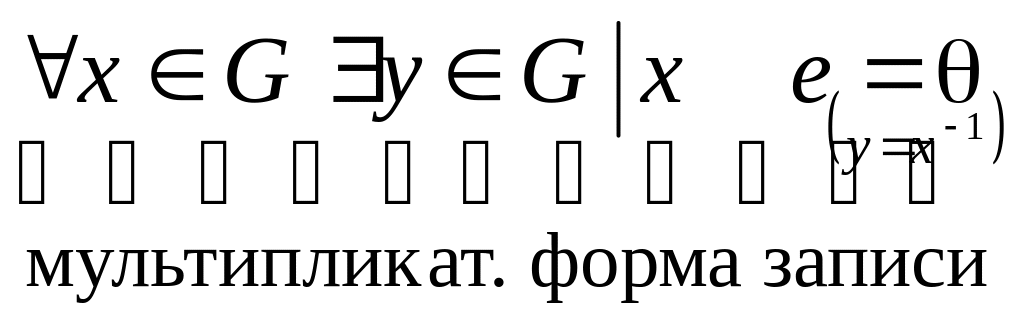Если введенная операция еще и коммутативная, т.е. x⊕y = y⊕x или (x⊙y = y⊙x), то группа называется абелевой.

Подмножество элементов G₁ группы G называется подгруппой, если:

1) х, уG₁  x⊙yG₁; 2) хG₁  x^1G₁.

(Здесь применена мультипликативная форма записи)

Подгруппа G₁ группы G сама по себе является группой. Простейшими (тривиальными) подгруппами любой группы является сама группа и группа, состоящая из одного элемента – нейтрального.