§5. Спектральное разложение эрмитового оператора. Теорема Гамильтона – Кэли

Пусть А – эрмитов оператор; ₁  ₂  …  _n собственные значения этого оператора и {е₁, е₂, …, е_m} – соответствующий им ортонормированный собственный базис. Тогда xV ; Ax = .

Def: Оператор Р_k: P_kx = (x,e_k)e_k, называется оператором-проектором или просто проектором на одномерное пространство, порожденное вектором {e_k}.

Свойства проекторов:

1. P_k – самосопряженный (эрмитов).

◀ (P_kx, y) = ((x,e_k)e_k, y) = (x,e_k)(e_k,y) = (x, e_k) = (x, (y,e_k)e_k) = (x, P_ky) ▶

2. = P_k. ◀ = P_k(P_kx) = P_k(x,e_k)e_k = (x,e_k)Pe_k = (x,e_k)(e_k,e_k)e_k = (x,e_k)e_k = P_kx ▶

3. P_kP_j = 0, (x  j). ◀ P_kP_j x = P_k(P_j x) = P_k(x,e_j)e_j = (x,e_j)P_ke_j = (x,e_j) e_k = 0 ▶

Для операторов-проекторов P_k имеем:

.

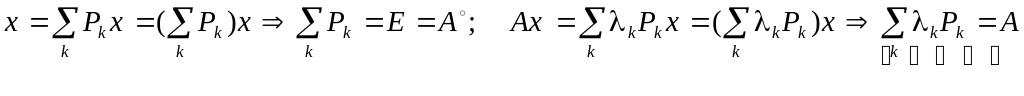Такое представление эрмитового оператора А называется его спектральным разложением . Обратим еще внимание: .

Def: Пусть Р(λ) – произвольный полином р^й – степени, т.е. . Тогда определим полином от оператора слеующим образом: .

Тº. (Гамильтона-Кэли). Эрмитов оператор А является корнем своего

характеристического полинома: если .

◀ ▶

§6. Положительные операторы. Корень m-й степени из оператора

Def: Эрмитов оператор А называется положительным, если хV, (Ax, x)  0. Если, кроме того, из (Ax, x) = 0  x = , то А называют положительно определенным оператором (Обозначается: A  0, A > 0 соответственно).

Тº. Каждое собственное значение положительного (положительно определенного)

оператора неотрицательно (положительно).

◀ Если λ – собственное значение А, то x такой, что ||x|| = 1, (Ax, x) =  (было доказано), отсюда следует утверждение теоремы ▶

Def: Корнем m-й степени из оператора А называется такой оператор В, что В^m = A.

Тº. Если А – положительный эрмитов оператор (А  0), то mN существует

положительный эрмитов оператор

◀ Пусть _k  собственные значения А (k =1, 2, 3,…, n) и {e_k}  ортонормированный собственный базис, (спектральное разложение) и при этом _k  0. Рассмотрим оператор . Изучим свойства оператора В. Оператор В:

а) эрмитов:

;

б) положителен:

;

в) . Теорема доказана. ▶

Примечание: В ортонормированном базисе {e_k} из собственных векторов матрица оператора А и матрица А^1/m имеют вид: ,

.

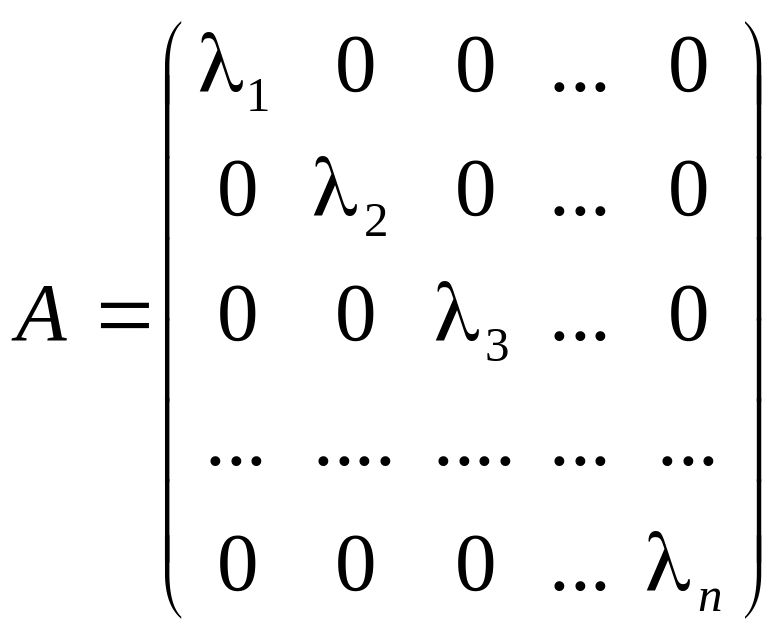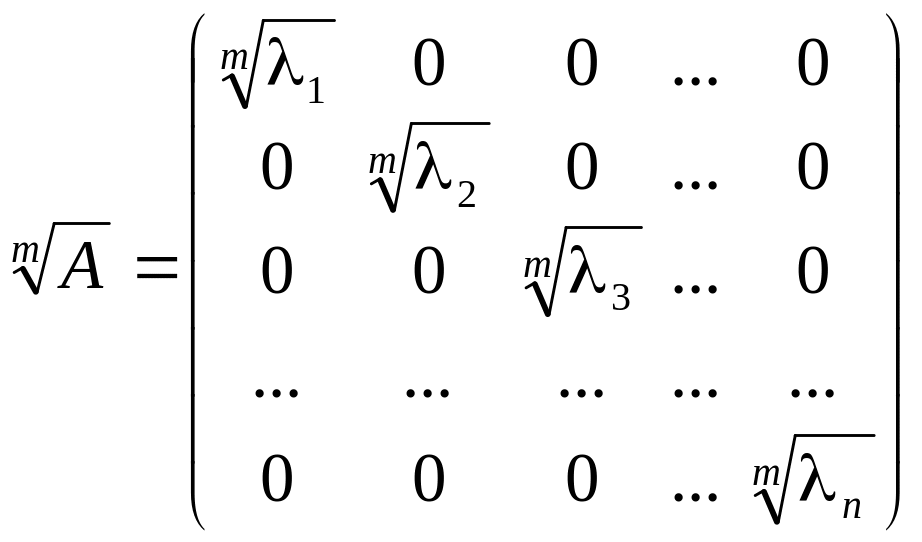Эрмитовы Формы §1. Полуторалинейные эрмитовы формы

Def: Полуторалинейная форма В(х, у) называется эрмитовой, если x, yV: .

Мы уже отмечали: В(х, у) – полуторалинейные формы  А – линейный оператор такой, что В(х, у) = (Ах, у).

Тº. Для того, чтобы полуторалинейная форма В(х, у) была эрмитовой необходимо и

достаточно, чтобы оператор А (В(х, у) = (Ах, у)) был эрмитовым.

◀ Достаточность: Пусть А – эрмитов, т.е. А = А^*  В(х, у) = (Ах, у) = (х, Ау) = =

, т.е. форма В(х, у) – эрмитова.

Необходимость: Пусть форма эрмитова  (Ах, у) = В(х, у) = = = (х, Ау), т.е.

А – эрмитов ▶

Тº. Для того, чтобы форма В(х, у) была эрмитовой необходимо и достаточно, чтобы

В(х, х) была вещественной хV.

◀ В(х, у) – эрмитова  А – эрмитов. А – эрмитов  А(х, у)R ▶

предыдущая доказано ранее

теорема