§15. Дифференциальные операции 1го порядка

1. Для векторного поля A_i образуем градиент векторного поля , а затем получившийся тензор свернем по индексам i, j : .

Как известно, такая величина в векторном анализе называется дивергенцией векторного поля А ( divA ). Подобным образом можно получить дивергенцию тензорного поля любого ранга, выше нулевого.

Результирующее тензорное поле имеет ранг на единицу меньший, чем исходное поле.

Для тензорного поля ранга r можно получить r различных тензорных полей (r – 1)^го ранга типа «дивергенции» в зависимости от того, какой из индексов исходного поля сворачивается с индексом дифференцирования: .

2. В векторном анализе известна такая дифференциальная операция, как rotA = A. В тензорном представлении . Оператором можно действовать на тензор любого ранга выше нулевого и затем сворачивать индекс l с одним из индексов этого тензора. Результирующее тензорное поле имеет тот же ранг, что и исходное.

Для тензорного поля ранга r можно получить r различных тензорных полей r^го ранга типа «ротор» в зависимости от того с каким из индексов исходного поля сворачивать индекс l.

.

3. Схематически операции градиента, дивергенции и ротора тензорного поля произвольного ранга можно задать следующим образом:

(gradT…)_i = ,

(divT…_i…) = ,

(rotT…_l…) = .

§16. Дифференциальные операции 2го порядка

1. Для скалярной функции φ: , и такая величина называется лапласианом функции.

Аналогично можно ввести лапласиан произвольного тензора ранга r и получить тензорное поле того же ранга:

Рассмотрим divrotA, где А – произвольное векторное поле:

Div rotA =

.

Равенство подчеркнутых выражений позволяет заключить, что divrotA = 0 для любого векторного поля А.

Аналогичное тождество имеет место для тензорного поля любого ранга (кроме нулевого): .

3. Проверим справедливость тождества: rot rot = grad div  Δ .

◀ (rot rot A)_i =

(divA)  (A)_i = (grad divA)_i  (A)_i = (grad divA  A)_i ▶

Аналогичное тождество можно записать и для произвольного тензорного поля.

§17. Интегральные формулы тензорного анализа

1. В векторном анализе поток векторного поля через поверхность S определяется как: (здесь – орт нормали к поверхности S). При этом поток векторного поля это скаляр.

Аналогично можно определить поток тензорного поля ранга r через поверхность S, как .

При этом поток тензорного поля ранга r через поверхность S это тензор (r – 1)^го ранга (покажите, что поток это тензор). Всего существует r различных полей ранга (r – 1) типа «поток» в зависимости от того по какому индексу тензора Т идет свертка.

2. Для векторных полей известна формула Гаусса-Остроградского:

.

Для тензорных полей существует r формул типа «Гаусса-Остроградского»

(справа и слева немой индекс должен быть один и тот же)

3. Формула Стокса для векторного поля имеет вид .

Та же формула в тензорной записи выглядит так: .

Формула Стокса может быть записана и для тензорных полей ранга r:

.

Всего может быть записано r формул типа «Стокса».

§18. Тензоры (задачи)

1. Показать, что произведение скаляра на тензор 2-го ранга является тензором 2-го ранга.

2. Показать, что величина (где - тензор 3-го ранга, – тензор 2-го ранга) является вектором.

3. Доказать инвариантность свойств антисимметрии антисимметричного тензора 2-го ранга .

4. Показать, что произведение тензоров 3-го ранга и 2-го ранга является тензором 5-го ранга.

5. Компоненты тензора Т_ik в некотором ортонормированном базисе образуют матрицу и, в том же базисе, вектор В имеет координаты (1,2,3).

а) Разложить тензор Т_ik в сумму симметричного S_ik и антисимметричного тензоров. б) Найти:

6. Пользуясь аппаратом тензорной алгебры, проверить тождества:

7. Записать в векторной форме выражение:

8. Пользуясь аппаратом тензорной алгебры, проверить тождества:

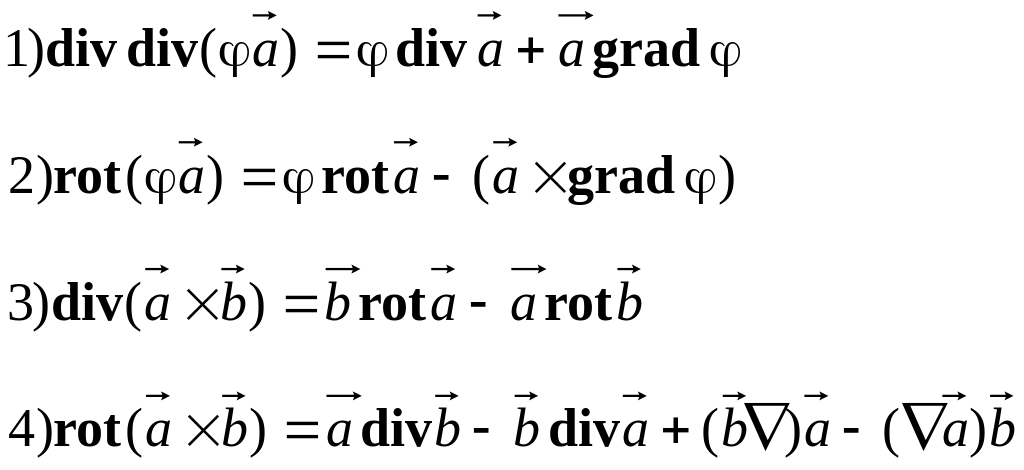
9. Пользуясь аппаратом тензорной алгебры, вычислить:

(радиус – вектор – , (постоянный вектор – ))

10) Найти дивергенции и роторы следующих векторов: .

(радиус – вектор – , (постоянный вектор – а, b))

11) Вычислить интеграл , где a, c – постоянные вектора, n(r) – орт нормали к поверхности S, которая ограничивает объем V.