Кінематичні пари механізму

Позначення кінематичної пари	Номери ланок, які утворюють кінематичну пару	Характер відносного руху ланок	Клас кінематичної пари
О1 А В В С С D	0–1 1–2 0–3 2–3 2–4 4–5 5–0	Обертальний Обертальний Обертальний Поступальний Поступальний Обертальний Поступальний	V V V V V V V

За формулою П.Л. Чебишева [1, 2, 3, 11] визначимо ступінь рухомості механізму:

(1.1)

де – кількість рухомих ланок механізму;

– кількість кінематичних пар V класу;

– кількість кінематичних пар ІV класу.

Оскільки , тоді в даному механізмі має бути одна початкова ланка. За початкову згідно з технічним завданням приймаємо ланку 1. Розкладаємо механізм на структурні групи Ассура. Перш за все відокремлюємо ланцюг, який складається з двох ланок 4, 5 і трьох кінематичних пар (С, С, D), які утворюють групу II класу другого порядку ІV виду (рис. 1.1, в). Далі відокремлюємо ланцюг, який складається з ланок 2, 3 (рис. 1.1, б) і трьох кінематичних пар (А, В, В). Ця група є групою II класу другого порядку III виду. Кривошип 1 разом зі стояком 0 утворюють механізм І класу (рис. 1.1, а).

У цілому механізм, який розглядаємо, є механізмом II класу. Для такого механізму можна записати формулу будови:

І(0, 1)→ІІ(2, 3) →ІІ(4, 5),

де цифрою І позначено механізм першого класу, цифрою II – клас групи

Рис. 1.1. Схеми механізму І класу (а) та груп Ассура ІІ класу другого порядку ІІІ (б) і IV (в) видів

Ассура. Номери ланок, що входять до складу механізму І класу та груп, взято у дужки.

2. Кінематичний аналіз шарнірно-важільного механізму

2.1. Побудова дванадцяти положень механізму

Кінематичну схему механізму будуємо в масштабі:

,

де – дійсна довжина кривошипа О₁А, м;

– довжина відрізка в мм, який зображає кривошип на плані механізму.

Інші відрізки кінематичної схеми:





.

Побудову кінематичної схеми починаємо з елементів нерухомої ланки. З точки О₁ (аркуш 1 (додаток А)) проводимо траєкторію центра шарніра А. Приймаємо положення кривошипа 1, для якого і повзун 5 знаходиться в крайньому лівому положенні, за початкове і будуємо дванадцять рівновіддалених положень кривошипа. Через отримані точки проводимо прямі , які визначають положення всіх інших ланок. Методом засічок знаходимо положення центра мас куліси 2. З’єднавши отримані точки плавною кривою, одержимо траєкторію точки .

Будуємо ще одне положення механізму, у якому повзун 5 знаходиться в крайньому правому положенні .

2.2. Побудова планів швидкостей для дванадцяти положень механізму

Побудову планів швидкостей розглянемо на прикладі шостого положення механізму. З полюса (див. аркуш 1 (додаток А) або рис. 2.1) плану швидкостей за напрямом обертання кривошипа перпендикулярно відкладаємо в масштабі вектор швидкості точки А, величина якого:

,

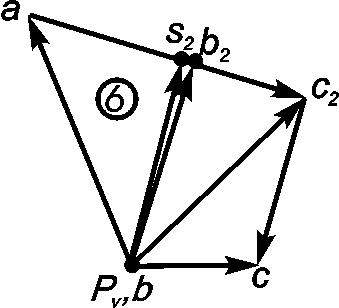
Рис. 2.1. План швидкостей для шостого положення механізму

де –кутова швидкість кривошипа, .

Приймаємо довжину відрізка, який зображає вектор швидкості точки А, Тоді масштаб плану швидкостей:

.

Швидкість точки B₂, яка лежить на кулісі АС і в даний момент збігається з точкою В, що належить каменю 3 чи стояку 0, визначаємо з рівнянь:

(2.1)

З точки а проводимо напрям вектора відносної швидкості (перпендикулярно до АВ), а через те, що , то з полюса проводимо напрям вектора швидкості (паралельно АВ). Точка перетину цих ліній і є шукана точка , а відрізки і відповідно у масштабі зображають вектори швидкостей і , тобто:



.

Для визначення швидкості точки С₂, яка належить кулісі 2 і в даний момент збігається з точкою С, що належить ланкам 4 і 5, використаємо теорему подібності плану швидкостей ланці, на підставі якої можна скласти пропорцію:

.

Тоді

.

Відклавши від точки а на продовженні відрізка відрізок , знаходимо положення точки , поєднавши яку з полюсом , отримаємо в масштабі швидкість точки С₂:

.

Швидкість точки С, яка належить повзунам 4 і 5, можна виразити через швидкості точок С₂ і С₀. Вектор швидкості точки С₂ відомий за величиною і за напрямом; швидкість точки С₀, що належить стояку і також збігається з точкою С, . Тоді можна записати векторні рівняння:

(2.2)

На плані швидкостей з точки проводимо паралельно кулісі АС пряму, яка визначає напрям швидкості , а з полюса проводимо лінію паралельну напрямній, що визначає напрям швидкості точки С відносно стояка. Відрізки і у масштабі зображають вектори швидкостей:



.

Для визначення швидкості центра мас S₂ куліси використаємо теорему подібності плану швидкостей ланці, склавши пропорцію:

, (2.3)

з якої знаходимо

.

З’єднавши точку з полюсом плану швидкостей, отримаємо відрізок , який у масштабі визначає значення швидкості:

.

Значення кутової швидкості куліси знаходимо за формулою

.

Щоб визначити напрям кутової швидкості , розглянемо обертання ланки 2 відносно точки А. Напрям руху точки В₂ відносно точки А визначається вектором швидкості . Подумки переносимо цей вектор у точку В механізму і вважаємо точку А нерухомою. Отже, ланка АС відносно точки А обертається за годинниковою стрілкою.

Плани швидкостей для інших положень механізму будуємо аналогічно (див. аркуш 1 (додаток А)). Отримані значення відрізків, які зображають вектори швидкостей, і значення швидкостей наведені у табл. 2.1.

Таблиця 2.1

Визначення швидкостей різних точок і ланок механізму

Позначення	Положення механізму
	0	1	2	3	4	5	6	7	8	9	10	11
	70,70	64,00	43,50	19,00	6,50	32,00	55,30	68,00	67,00	40,00	15,00	53,00
	1,60	0,96	0,65	0,28	0,10	0,48	0,83	1,02	1,01	0,60	0,22	0,80
	0,00	31,50	56,50	68,00	70,00	63,00	44,00	17,50	24,50	58,50	68,50	40,50
	0,00	0,47	0,85	1,02	1,05	0,95	0,66	0,26	0,37	0,88	1,03	0,61
	70,70	69,00	58,50	46,50	42,50	51,50	64,00	70,00	71,00	78,50	93,00	76,00
	1,06	1,03	0,88	0,70	0,64	0,77	0,96	1,05	1,07	1,12	1,39	1,14
	0,00	26,50	40,00	41,50	41,50	40,00	33,50	16,00	25,00	76,00	92,00	51,00
	0,00	0,40	0,60	0,62	0,62	0,60	0,50	0,24	0,37	1,14	1,38	0,76
	70,70	55,00	34,00	14,00	5,30	21,00	45,50	62,50	76,00	54,50	23,00	75,00
	1,06	0,83	0,51	0,21	0,08	0,32	0,68	0,94	1,14	0,82	0,35	1,12
	70,70	63,50	43,50	22,00	12,50	33,00	55,00	68,50	68,00	56,00	61,00	62,50
	1,06	0,95	0,65	0,33	0,19	0,49	0,83	1,03	1,02	0,84	0,92	0,94
	0,00	1,41	2,23	2,50	2,54	2,38	1,83	0,85	1,48	4,37	5,44	2,73