§8. Зв’язок між розв’язками неоднорідних і однорідних систем.

Нехай дана система лінійних неоднорідних рівнянь

(2)

Система лінійних однорідних рівнянь

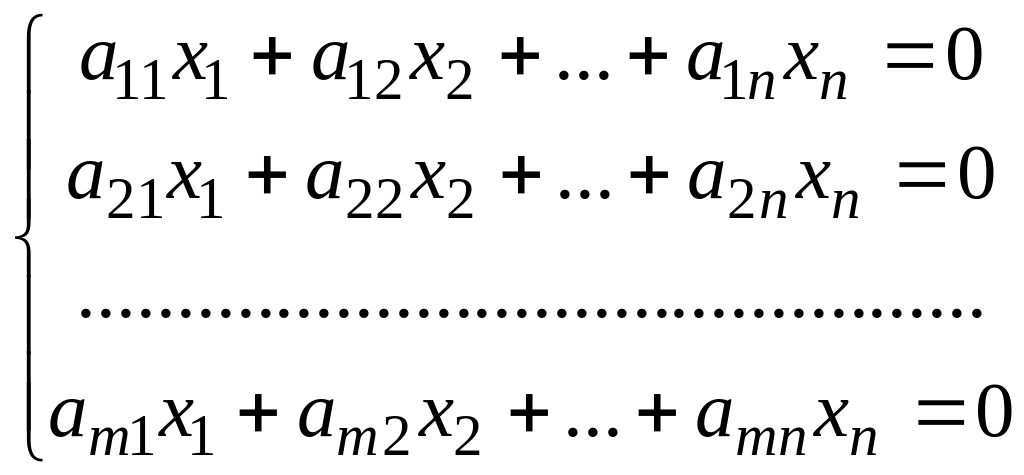(3)

яка одержується з системи (2) заміною вільних членів нулями, називається зведеною системою для системи (2).

Зв’язок між розв’язками систем (2) і (3):

1. Сума будь-якого розв’язку системи (2) з будь-яким розв’язком зведеної системи (3) знову буде розв’язком системи (2).

2. Різниця будь-яких двох розв’язків системи (2) є розв’язком для зведеної системи (3).

Наслідок. Знайшовши один розв’язок системи лінійних неоднорідних рівнянь (2) і додавши до нього кожний з розв’язків зведеної системи (3), ми одержимо всі розв’язки системи (2).

Приклад.

Знайти загальний та один частинний розв’язок системи лінійних рівнянь:

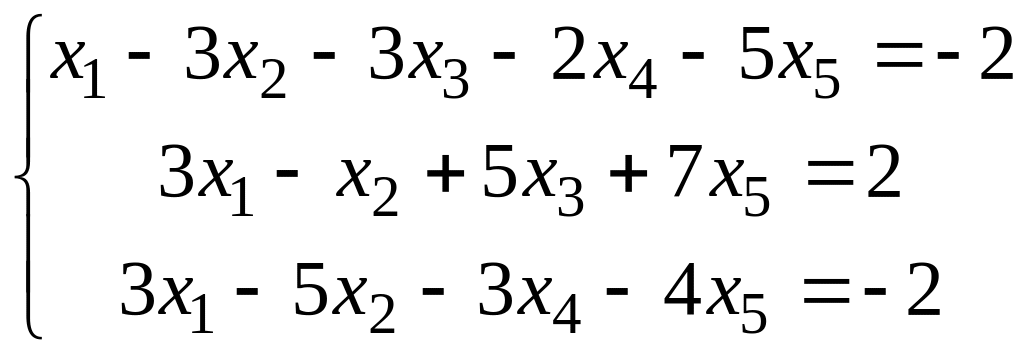
Знайдемо загальний розв’язок відповідної однорідної системи рівнянь.

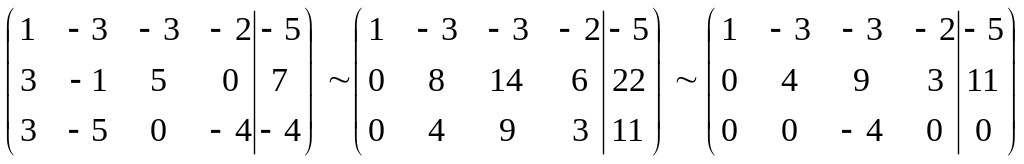
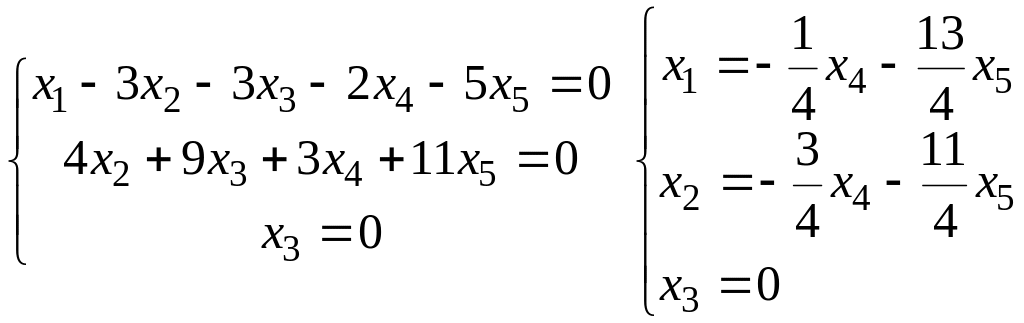
Загальний розв’язок СЛОР (-1/4x₄-13/4x₅, -3/4x₄-11/4x₅, 0,x₄,x₅),

x₄,x₅ є R.

Частинний розв’язок СЛР (1,1,0,0,0).

Загальний розв’язок СЛР (1-1/4x₄-13/4x₅, 1-3/4x₄-11/4x₅, 0,x₄,x₅),

x₄,x₅ є R.

§9. Лінійний многовид.

Означення. Нехай V – підпростір лінійного простору V, а х₀ – деякий вектор з V. Множина Р всіх векторів х=х₀+y, де y – будь-який вектор підпростору V, називається лінійним многовидом простору V.

Лінійний многовид Р утворюється шляхом зсуву підпростору V на вектор х.

Означення. Розмірністю многовиду Р називається розмірність того підпростору V, зсувом якого було одержано цей многовид.

Теорема 8. Множина розв’язків СЛР є лінійним многовидом, одержаним шляхом зсуву підпростору V розв’язків відповідної СЛОР на вектор х₀, де х₀ – один довільно вибраний і фіксований розв’язок СЛР.

х є Р ( Р=х₀+V={x₀+aa є V} )

Приклад.

Побудувати лінійний многовид Р розв’язків такої СЛР:

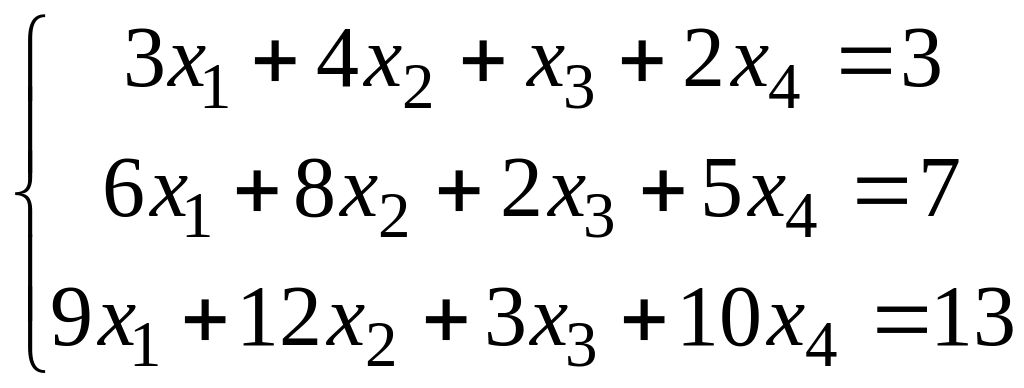
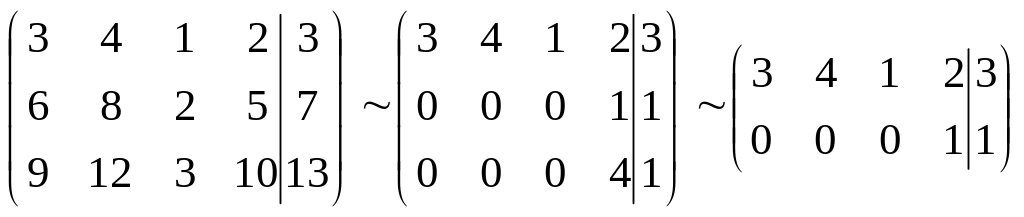
Загальний розв’язок СЛР (х₁,х₂,-3х₁-4х₂+1,1).

Загальний розв’язок СЛОР (х₁,х₂,-3х₁-4х₂,0).

X1	X2	X3	X4
1	0	-3	0
0	1	-4	0

L((1,0,-3,0),(0,1,-4,0)), Р=(0,0,1,1)+L((1,0,-3,0),(0,1,-4,0)).

Розділ 2. Матриці та дії над матрицями. §1. Матриці.

Означення. Матрицею називається прямокутна таблиця, яка складається з елементів даного поля.

Загальний вигляд матриці:

A = 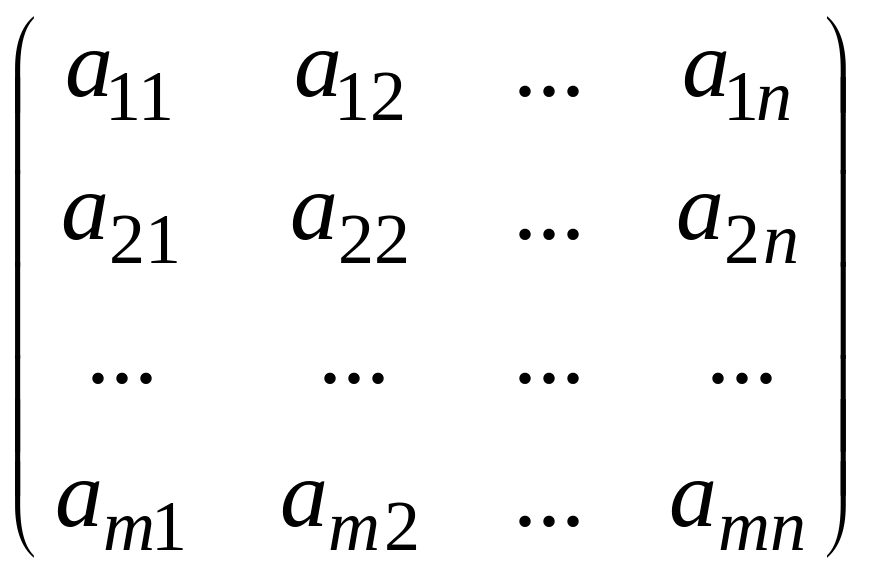= (а_ij) , А = (a₁,a₂,…,a_n), В =

де а_ij ,а_i ,b_j - елементи матриці.

Якщо в матриці А кількість рядків дорівнює кількості стовпців, тобто m=n, то вона називається квадратною матрицею n-го порядку; якщо ж mn, то матриця називається прямокутною матрицею розміру m*n. Головною діагоналлю квадратної матриці n-го порядку називається діагональ, яка йде від лівого верхнього кута до нижнього правого, тобто яка складається з елементів а₁₁,а₂₂,…,а_nn.

Означення.Квадратна матриця D=(d_ij) n-го порядку називається діагональною, якщо всі її елементи, які не належать головній діагоналі, дорівнюють нулю:

i, j ( i j => d_ij=0).

Елемент головної дігоналі матриці називають i-им дігональним елементом.

Діагональна матриця називається скалярною, якщо елементи її головної діагоналі рівні між собою. Діагональна матриця : D =

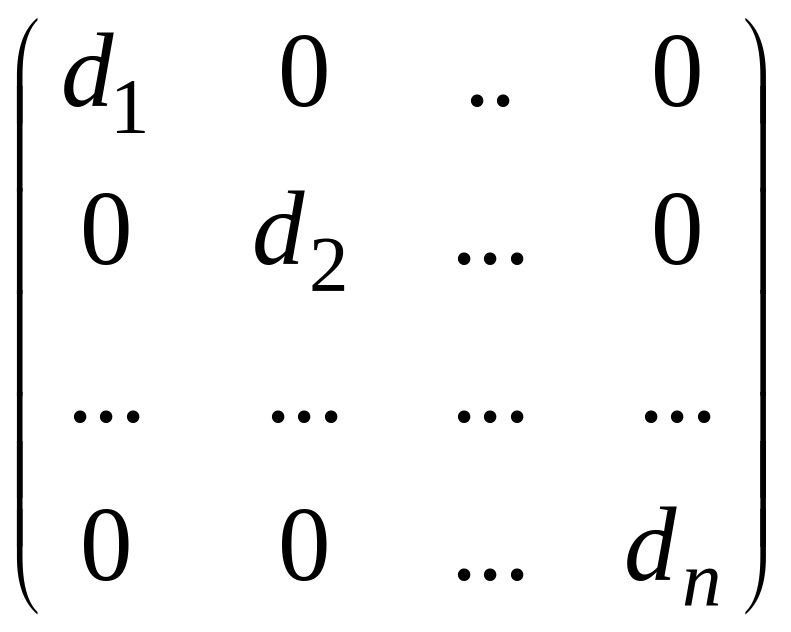
Скалярна матриця: K =

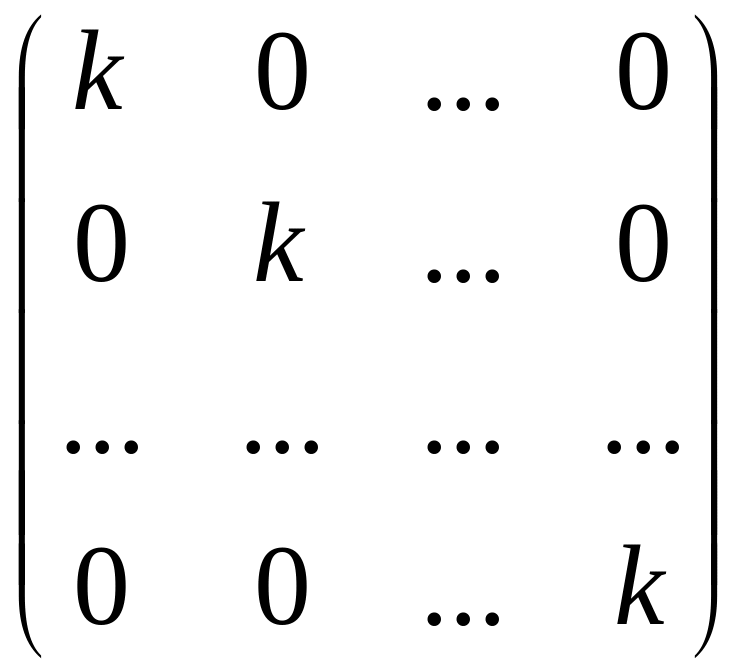
Частинним випадком скалярної матриці є одинична E і нульова O:

E =  =

Дві матриці називаються рівними, якщо рівні відповідні їх елементи.

Від матриці А можна перейти до матриці А :

A =

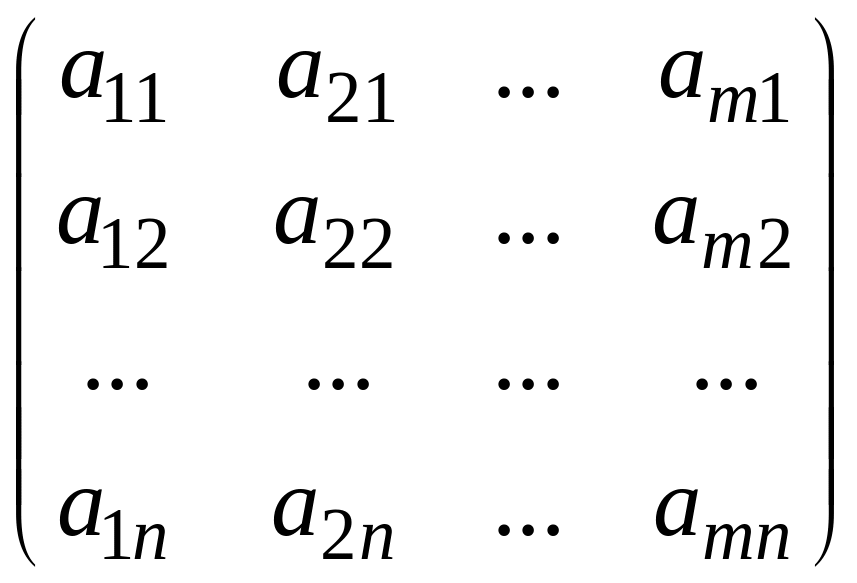
в якій рядки є стовпцями, а стовпці – рядками матриці А. Перехід від матриці А до матриці A називається транспонуванням матриці А, а матриця А називається транспонованою для матриці А. Якщо матриця А – квадратна, то її транспонування – це заміна кожного рядка матриці на відповідний стовпчик.

Якщо А – довільна квадратна матриця і A=A,

то А називається симетричною; якщо A=-А,

то А - кососиметрична.

Квадратна матриця ортогональна, якщо АА=AA=E.

Матриця називається ідемпотентною, якщо А²=А.