§3. Елементарні перетворення.

Означення. Елементарними перетвореннями системи лінійних рівнянь називаються такі перетворення:

1. перестановка місцями (транспозиція) двох рівнянь системи;

2. множення будь-якого рівняння системи на число, відмінне від нуля;

3. додавання до одного рівняння системи іншого її рівняння, помножене на деяке число;

4. викреслення невизначеного рівняння.

Теорема Гауса. Елементарні перетворення системи не змінюють множину її розв’язків, тобто приводять нас до рівносильної системи.

Ідея метода Гауса СЛР полягає в тому, що за допомогою елементарних перетворень переходимо від даної системи до системи виду трикутника або трапеції і розв’язуємо одержану систему, а оскільки вона рівносильна даній, то одержуємо розв’язок (множину розв’язків) початкової системи.

Алгоритм:

1. якщо в системі є суперечливе рівняння, то система несумісна;

2. якщо в системі є невизначене рівняння, то викреслюємо його;

3. робимо коефіцієнт а₁₁0;

4. перше рівняння залишаємо, наступні рівняння утворюємо так:

перше рівняння а₁₁х₁+а₁₂х₂+…+а_1nх_n=b₁ домножуємо на

–а_1n/а₁₁ і додаємо до наступних.

В результаті одержимо систему:

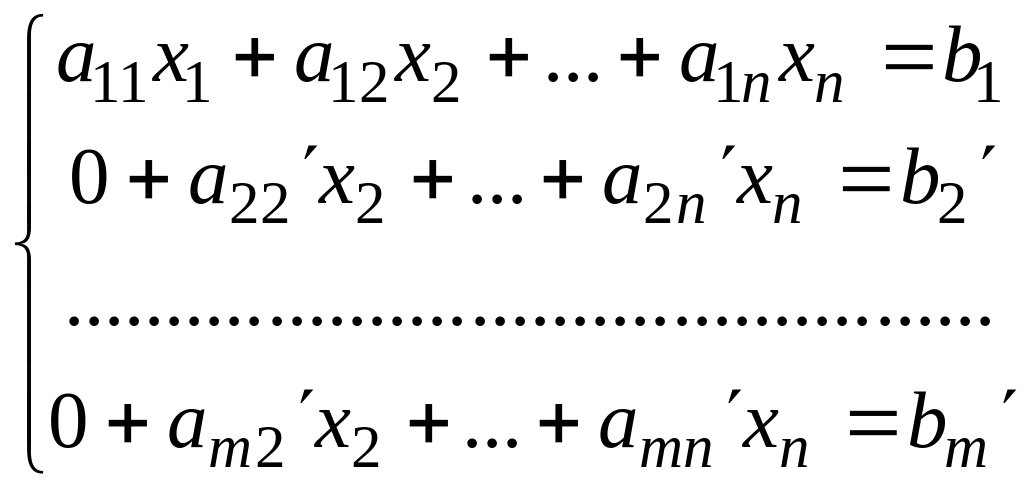
Далі аналогічно беремо рівняння a₂₂x₂+…+a_2nx_n=b₂ і обнуляємо коефіцієнти а_k2, k3.

Отже, дану систему ми звели до діагонального виду

в якій діагональні елементи а_ii0(i=1,…,r,r<=k).

В результаті цих перетворень, якщо матриця СЛР зводиться:

1. до виду трикутника, то СЛР має єдиний розв’язок;

2. до виду трапеції, тоді СЛР має безліч розв’язків.

Змінні, через які ми виражаємо всі інші змінні називаються вільними змінними.

Для зручності обчислень будемо використовувати матриці, бо перетворення з рядками зводяться до переворень з коефіцієнтами.

Приклад.

1. Розв’язати систему лінійних рівнянь методом Гауса:

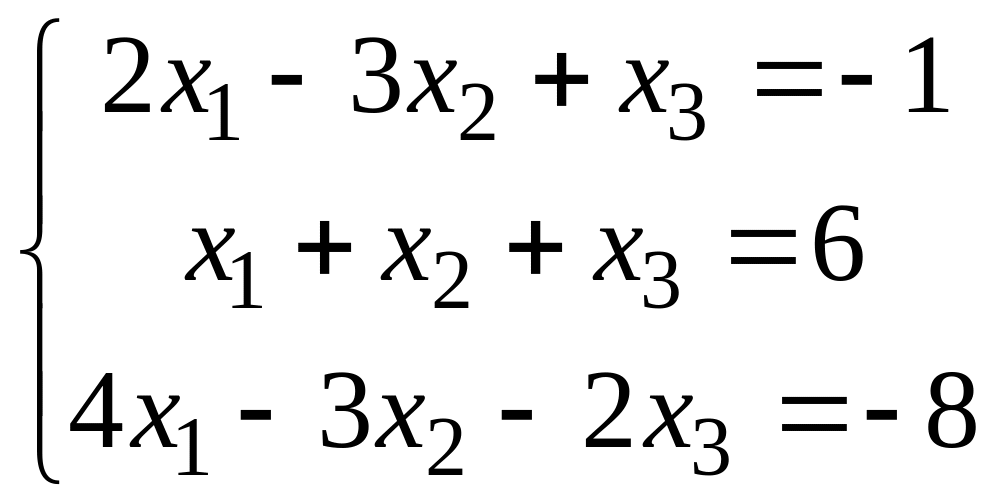
Дана система звелась до виду трикутника. Її розв’язок (1,2,69/23).

2. Розв’язати систему лінійних рівнянь методом Гауса:



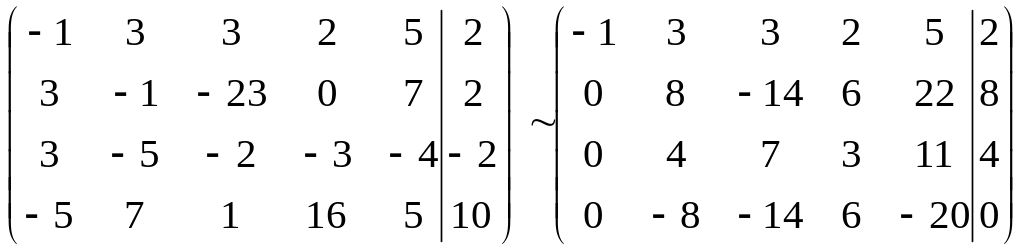
х₁=-12-44 3/4x₃+26 3/4x₄,

x₂=-19-39 1/4x₃+18 1/4x₄,

x₃,x₄ є R,

x₅=4+14x₃-6x₄.

Cистема звелась до виду трапеції.

Її розв’язок (-12-44 3/4x₃+26 3/4x₄, -19-39 1/4x₃+18 1/4x₄, x₃,x₄,

4+14x₃-6x₄), х₃,x₄ є R.

3. Розв’язати систему лінійних рівнянь методом Жордана-Гауса:

Отже її розв’язок (2,-3,-1).

4. Розв’язати систему лінійних рівнянь:

Дана система містить суперечливе рівняння, отже вона розв’язків немає.

§4. Векторні простори.Арифметичний n-мірний векторний простір.

Означення. Множина із введеними на ній алгебраїчними операціями називається алгеброю.

Алгебри класифікують за властивостями операцій.

Означення. Mножина G із введеною на ній алгебраїчною операцією * називається групою, якщо виконуються такі властивості:

1) асоціативність операції a,b,c є G ((a*b)*c=a*(b*c));

2) нейтральний елемент a є G e (a*e=e*a=a);

3) симетричний елемент a є G a (a*a=a*a=e).

Означення.Група називається абелевою, якщо операція комутативна, тобто:

a b (a*b=b*a).

Означення.Множина <K,+,* > називається кільцем, якщо:

1) <K,+> - абелева група;

2. * - асоціативна;

3. дистрибутивні закони

a,b,c є K ( (a+b)c=ac+bc)

( c(a+b)=ca+cb).

Означення.Кільце називається комутативним, якщо операція множення комутативна.

Означення.Комутативне кільце з одиницею, в якому

a ≠ 0  a^-1 (a*a^-1=1), називається полем.

Приклади алгебр.

1. R–кільце (по додаванню і множенню), Q - комутативне кільце;

2. Z - комутативне кільце (по додаванню і множенню);

3. Z,Q – абелеві групи;

4. R – поле.

Mножина всіх n–мірних числових векторів - абелева група відносно додавання.

Означення. Векторним (лінійним) простором над полем Р називають множину елементів довільної природи, в якій введено операції додавання і множення на елементи поля (скаляри) і виконуються аксіоми:

1) <V,+> - абелева група;

2) Операція множення на скаляр асоціативна

k,l є P , a є Vn ((kl)a=k(la));

3) a є Vn (1*a=a), 1 P;

4) Операція множення на скаляр дистрибутивна відносно додавання елементів множини Vn

k є P a,b є Vn (k(a+b)=ka+kb);

5) Операція множення на скаляр дистрибутивна відносно додавання скалярів k,l є P a є V ((k+l)a=ka+kb).

Якщо поле Р - це поле дійсних чисел, то простір Vn називається дійсним векторним (лінійним ) простором.

Означення.Множина Vn всіх n-мірних числових векторів з координатами з поля Р з введеними на ній операціями додавання векторів і множення вектора на число з поля Р називається n-мірним арифметичним простором над полем Р.

Приклади векторних просторів:

1. Vn - векторний простір;

2. Множина всіх дійсних функцій, неперервних на відрізку [а,в] - дійсний векторний простір;

3. Поле С комплексних чисел відносно додавання і множення – комплексний векторний простір;

4. Сукупність R[x] всіх многочленів від змінної х з дійсними коефіцієнтами є дійсним лінійним простором;

5. Сукупність матриць n-го порядку над полем Р є лінійним простором над Р відносно додавання і множення на скаляри поля Р(буде показано далі).

Означення.Непорожня підмножина V векторного простору Vn називається підпростором простору, якщо вонa є лінійним простором відносно операцій,

введених у Vn.

Ознака лінійного підпростору – замкненість відносно введеної операції:

V–підпростір Vn 1) a,b є V ( a+b є V );

2) k є P a є V ( ka є V ).

Приклади підпросторів:

1. Множина, яка складається лише з нульового елемента є лінійним підпростором будь- якого векторного простору (нульовий підпростір);

2) Векторний простір є своїм підпростором;

3) В арифметичному просторі Vn множина V (m<n ) всіх векторів виду (а₁,а₂,…,а_n,0,...,0) є лінійним підпростором;

4) Простір розв’язків системи лінійних однорідних рівнянь є підпростором (буде показано далі).