§6. Інваріантні підпростори. Власні вектори і власні значення лінійного оператора.
Означення. Підпростір U лінійного простору Vn називається інваріантним відносно оператора А, якщо UAU, тобто якщо образ хА довільного вектора х з U міститься в U.
Приклади.
V- довільний векторний простір. Кожний підпростір простору V інваріантний відносно тотожнього оператора Е і нульового
оператора О.
V- довільний векторний простір, А – лінійний оператор у просторі V. Область значень VA і ядро KerA оператора А інваріантні підпростори відносно оператора А.
Означення. Вектор а 0, який задовольняє умові аА = а, де є Р, називається власним вектором оператора А, а число - власним значенням оператора А, яке відповідає власному вектору а.
Теорема 9. Власні вектори а1,а2,…,аm лінійного оператора А, яким відповідають попарно різні власні значення 1,2,…,m утворюють лінійно незалежну систему.
§7. Характеристичне рівняння лінійного оператора.
Нехай А=(аij) – деяка матриця n-го порядку над полем Р.
Е – одинична матриця порядку n, - деяке невідоме, тоді матриця А-Е називається характеристичною матрицею матриці А.
А
=
Визначник А-Е є многочленом n-го степеня від .
Рівняння А-Е =0 називається характеристичним рівнянням матриці А, а його корені називаються характеристичнимим коренями цієї матриці.
Лема. Характеристичні рівняння і характеристичні корені подібних матриць однакові.
Нехай А є лінійним оператором n-мірного простору Vn, а А – матриця цього лінійного оператора в довільно вибраному базисі {e1,e2,…,en}.
Характеристичне рівняння А-Е =0 матриці А називається характеристичним рівнянням оператора А, а його корені - характеристичними коренями оператора А.
Означення. Весь набір характеристичних коренів оператора А називається спектром лінійного опереатора А.
Лінійний оператор А в n-мірному просторі V над полем Р має простий спектр, якщо в полі Р існує n різних характеристичних коренів цього оператора.
Теорема 10. Для того, щоб число k є Р було власним значенням лінійного оператора А, необхідно і достатньо, щоб воно було характеристичним коренем.
§8. Лінійний оператор з простим спектром.
Нехай лінійний оператор А n-мірного простору Vn має n лінійно незалежних власних векторів а1,а2,…,аn. Очевидно, що система з власних векторів утворює базис Vn. Нехай власним векторам а1,а2,...,аn відповідають власні значення 1,2,…,n, тобто аiА=1е1+2е2+…+nеn. Тоді в базисі {а1,а2,…,аn} оператор А задається діагональною матрицею
А
=
Цікаво, чи кожну матрицю лінійного оператора можна звести до діагонального виду?
Теорема 11. Для того, щоб матриця лінійного оператора зводилась до діагонального виду, необхідно і достатньо, щоб існував базис з власних векторів, в якому вона матиме діагональний вид.
Приклад.
Показати, що відображення простору R в себе, яке переводить довільний вектор х=(х1,х2,…,хn) у вектор (х)=(х2+х3,2х1+х3,3х1-х2+х3) є лінійним. Знайти його матрицю в базисі е1=(1,0,0), е2=(0,1,0), е3=(0,0,1).
Покажемо, що виконується
1. (х+y)=(x)+(y) i 2. (kx)=k(x).
Нехай y=(y1,y2,…,yn), (y)=(y2+y3,2y1+y3,3y1-y2+y3), x+y=(x1+y1,x2+y2,x3+y3), kx=(kx1,kx2,kx3).
(x+y)=(x2+y2+x3+y3,2(x1+y1)+x3+y3,3(x1+y1)-(x2+y2)+x3+y3)= =(x2+x3+y2+y3,2x1+x3+2y1+y3,3x1-x2+x3+3y1-y2+y3)=(x)+(y);
(kx)=(kx2+kx3,2kx1+kx3,3kx1-kx2+kx3)=k(x2+x3,2x1+x3,3x1-x2+x3)= =k(x).
(e1)=(0,2,3)
(e2)=(1,0,-1)
A =
(e3)=(1,1,1)
2)
Довести
що, якщо
–
деяка матриця з лінійного простору М
квадратних матриць порядку 2 над полем
Р, то відображення 1
і 2
простору М, які визначені формулами
1(А) = А , 2(A) = A , є лінійним.
Знайти матриці цих відображень в базисі
e1
=
е2
=
е3
=
е4
=
Доводимо, що відображення 1 і 2 є лінійними
1(А+В)=(А+В) = A +B = 1(A)+2(B)
1(kA)=kA = k1(A)
Отже, 1 - лінійне відображення. Аналогічно
2(А+В)=(А+В)
= A
+B
= 2(A)+2(B)
2(kA)=kA = k2(A)
Отже, 2 - лінійне відображення.
1(e1)
=
=
1(e2)
=
=
1(e3)
=
=
1(e4)
=
=
Знаходимо матрицю лінійних операторів 1 і
= a11 + a12 + a13 + a14
a11=a a12=b a13=0 a14=0
= a21 + a22 + a23 + a24
a21=c a22=d a23=0 a24=0
= a31 + a32 + a33 +a34
a31=0 a32=0 a33=a a34=b
= a41 + a42 + a43 + a44
a41=0 a42=0 a43=c a44=d
A
=
Аналогічно
2(e1)
=
=
2(e2)
=
=
2(e3)
=
=
2(e4)
=
=
= a11 + a12 + a13 + a14
a11=a a12=0 a13=b a14=0
= a21 + a22 + a23 + a24
a21=0 a22=a a23=0 a24=b
= a31 + a32 + a33 + a34
a31=c a32=0 a33=d a34=0
= a41 + a42 + a43 + a44
a41=0 a42=c a43=0 a44=d
B
=
3)Довести, що якщо а=(1,2,3) – вектор з евклідового простору R над полем R і для х=(х1,х2,х3) є R (х)=(х,а)а=(х1+2х2+3х3)а, то відображення є лінійним. Знайти його матрицю в базисі b1=(1,0,1), b2=(2,0,-1), b3=(1,1,0).
(х+y)=(x+y,a)a=(x1+y1+2x2+2y2+3x3+3y3)a=
=(x1+2x2+3x3)a+(y1+2y2+3y3)a=(x)+(y)
(kx)=(kx1+2kx2+3kx3)a=k(x1+2x2+3x3)a=k(x)
Отже, - лінійне відображення.
Знаходимо матрицю відображення :
(b1)
= (
)
= 4(1,2,3) = (4,8,12)
(b2)
= (
)
= -1(1,2,3) = (-1,-2,-3)
(b3)
= (
)
=
3(1,2,3) = (3,6,9)
(4,8,12) = a(1,0,1)+a(2,0,-1)+c(1,1,0)
(-1,-2,-3)=d(1,0,1)+e(2,0,-1)+f(1,1,0)
(3,6,9)=k(1,0,1)+m(2,0,-1)+n(1,1,0)
A
=
4)Лінійне відображення простору R в базисі
а1=(0,0,1), а2=(0,1,1), а3=(1,1,1) має матрицю
А =
Знайти матрицю В цього відображення в базисі b1=(2,3,5), b2=(0,1,2), b3=(1,0,0).
B=TAT-1, де Т матриця переходу від базиса a до базиса b. Знаходимо цю матрицю.
(2,3,5)=k(0,0,1)+m(0,1,1)+n(1,1,1)
(1,0,0)=p(0,0,1)+q(0,1,1)+r(1,1,1)
(0,1,2)=e(0,0,1)+f(0,1,1)+g(1,1,1)
T
=
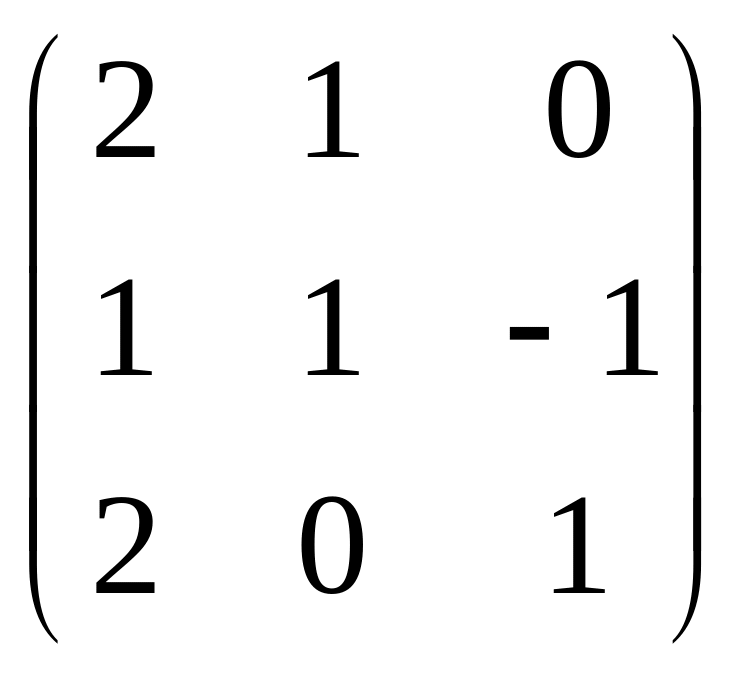
T-1
=
Перевірка
:
B
=
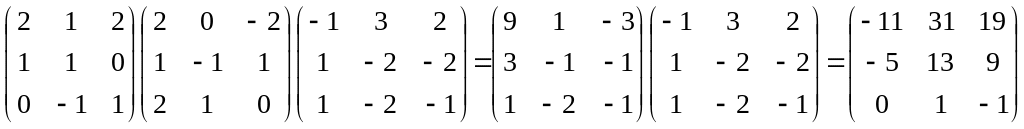
5)Лінійне відображення в базисі а1 = (-3,7), а2 = (1,-2) має матрицю А, а лінійне відображення в базисі b1 = (6,-7), b2 = (-5,6) має матрицю В. Знайти матрицю відображення в тому ж базисі, в якому дані координати векторів а1,а2,b1,b2.
e1 = t11a1+t12a2
e2 = t21a1+t22a2
1. (1,0) = t11(-3,7)+t12(1,-2)
(0,1) = t21(-3,7)+t22(1,-2)
T
=
T-1
=
Ae=
TAT-1=
=
2. (1,0)=t11(6,-7)+t12(-5,6)
(0,1)=t21(6,-7)+t22(-5,6)
T
=
T-1
=
B=TBT-1=
=
BA=
=
6)Чи зводиться матриця лінійного оператора до діагонального виду?
а)
А =
Запишемо характеристичне рівняння
А-Е=
= (-1-)(1-)(2-)
= 0
1 = -1 2 = 1 3 = 2
Одержали три різні власні значення, тому записуємо діагональну матрицю лінійного оператора
B
=
Знаходимо власні вектори, використовуючи означення:
х = хА = [x]A
1 = 1 (x1,x2,x3) = (x1,x2,x3)A = (x1,x2,x3)
Аналогічно для 2
2 = 2 2(x1,x2,x3) = (x1,x2,x3)A = (x1,x2,x3)
Аналогічно для 3
3 = -1 - 1(x1,x2,x3) = (x1,x2,x3)A = (x1,x2,x3)
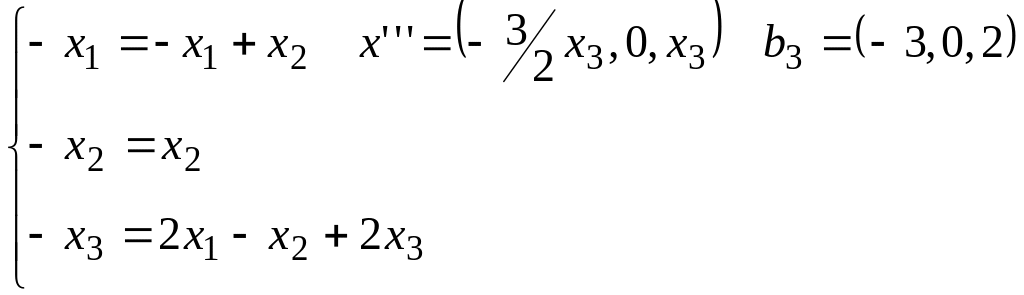
Власні вектори: {b1,b2,b3}.
b)
А =
А-Е
=
= (5-)(1-)(-5-)+24(1-)
=
= (1-)(-25+2+24)
= (-1)(+1)(-1)
= 0
1 = 1 2 = 1 3 = -1
Знаходимо власні вектори для 1,2:
1,2 = 1 (x1,x2,x3) = (x1,x2,x3)A
Із загального розв’язку СЛОР знаходимо фундаментальну систему розв’язків( власні вектори утворюють лінійно незалежну систему векторів)
-
X1
X2
X3
-2
1
0
-3
0
1
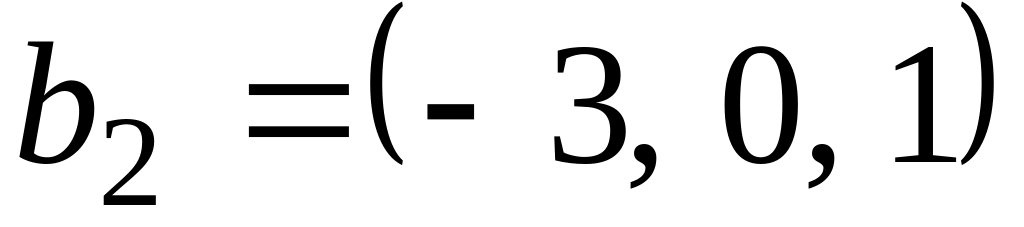
Знаходимо власний вектор для 3:
3 = -1-(x1,x2,x3) = (x1,x2,x3)A
Власні
вектори: {b1,b2,b3}
утворюють базис V3,
тому матриця лінійного оператора
зводиться до діагонального виду A =
с)
А =
А-Е
=
= (6-)(2+)+20+18-6(2+)-15-4(6-)
= =
(12+4-2)+38-12-6-15-24+4
=
=-3+42+12-17+2
= -3+42-5+2
= 0
1 = 1 2 = 1 3 = 2
1. 1,2 = 1 (x1,x2,x3) = (x1,x2,x3)A
x = (-x2,x2,x2) b1 = (-1,1,1)
2. 3 = 2 (2x1,2x2,2x3) = (x1,x2,x3)A
x = (-2x3,2x3,x3) b = (-2,2,1)
Матриця А не зводиться до діагонального виду, оскільки не існує базису, який складається з трьох власних векторів.
d)
A =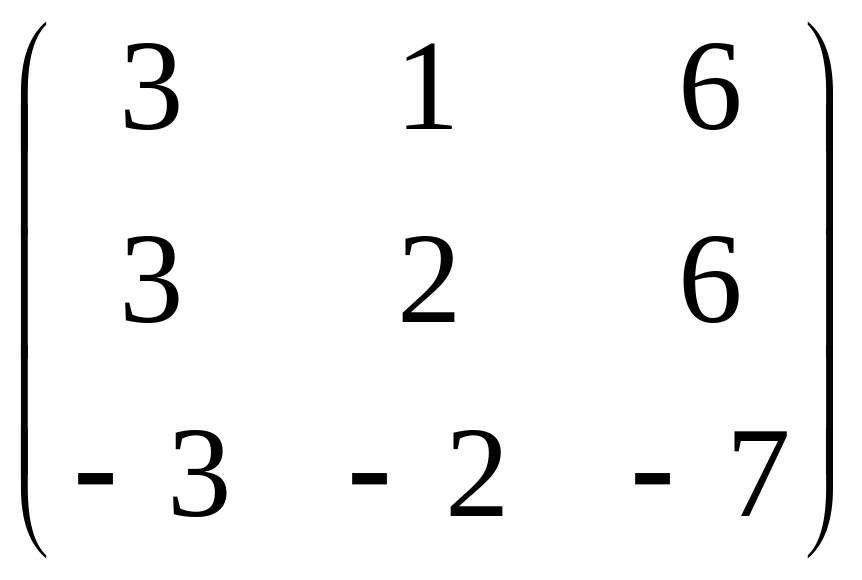
A-E
=
= (+3)(2-+1)=0
1=-3 2,3=1/2i /2 R,
Ми розглядаємо векторний простір над полем дійсних чисел, тому матриця до діагонального виду не зводиться.