§ 6. Матрична форма системи лінійних рівнянь.

Нехай дана система лінійних рівнянь

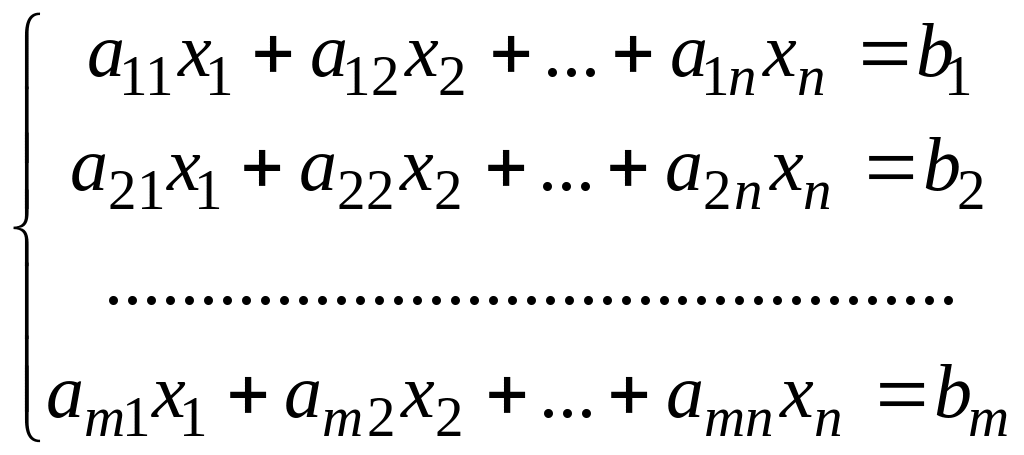
Дану систему можна записати у матричній формі

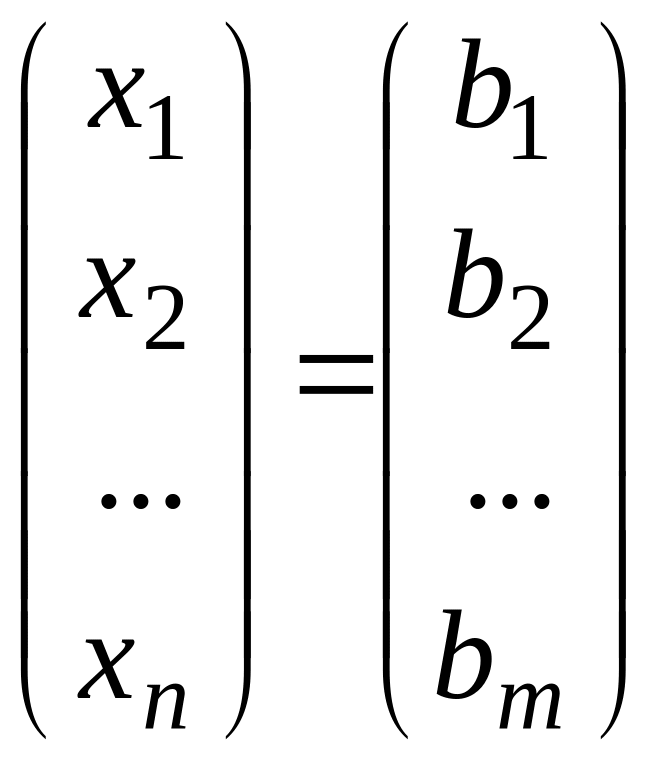
або скорочено АХ=В,

де А – матриця системи розміру m*n, а X і B – n- i m-мірні вектори-стовпці:

X = B =

які називаються вектором невідомих і вектором вільних членів відповідно.

Якщо В=О, то одержимо матричну форму СЛОР : АХ=О.

Щоб розвязати СЛР так званим “матричним методом”, необхідно розвязати матричні рівняння виду :

а) АХ=В, тоді домножимо обидві частини рівняння на А^-1 зліва

А^-1AX=A^-1B => EX=A^-1B =>X=A^-1B.

б) ХА=В, тоді домножимо обидві частини рівняння на А^-1 справа

XAA^-1=BA^-1 => XE=BA^-1 => X=BA^-1.

в) АХВ=С, тоді домножимо обидві частини рівняння на A^-1 зліва і на В^-1 справа.

А^-1AXBB^-1=А^-1CB^-1 => EXE=А^-1CB^-1 => X=А^-1CB^-1

Приклади.

1. Розв’язати рівняння :

Х =

ХА=В => XAA^-1=BA^-1 => X=BA^-1

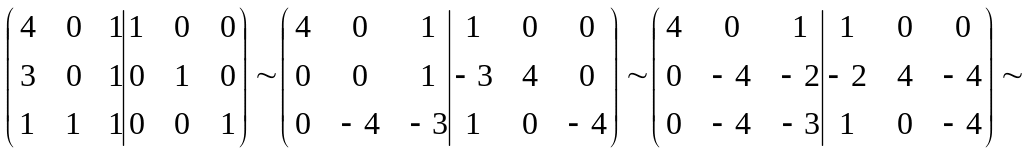
A =

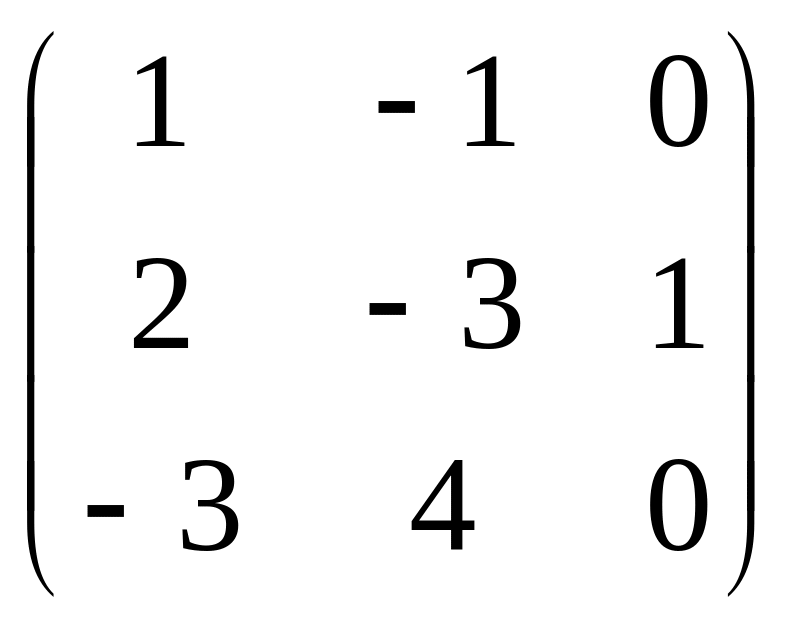
Перевірка:

X =

2) Розв’язати рівняння:

AX=B => A^-1AX=A^-1B² => X=A^-1B²

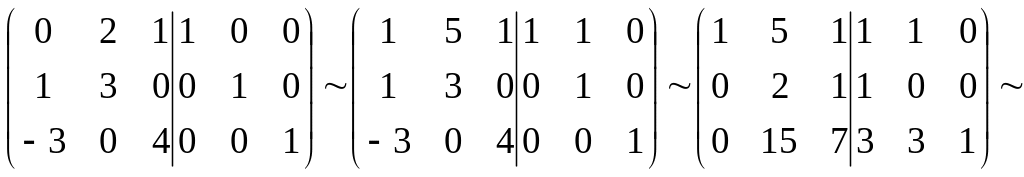
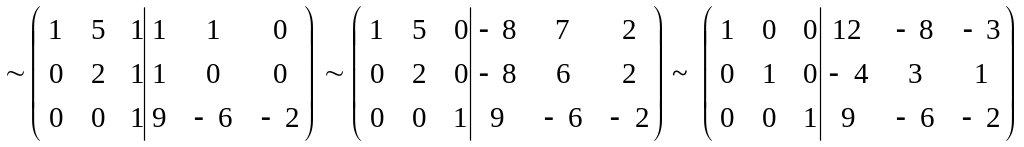
A^-1 =

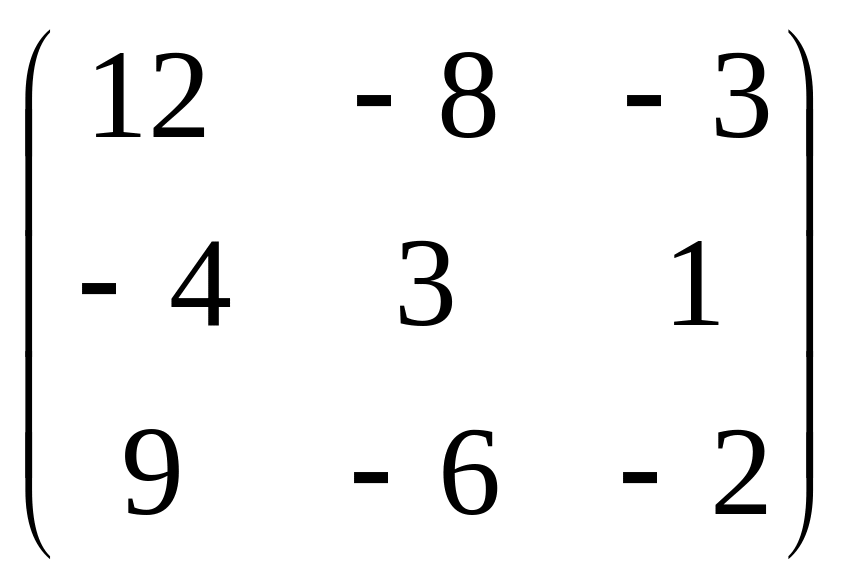
Перевірка :

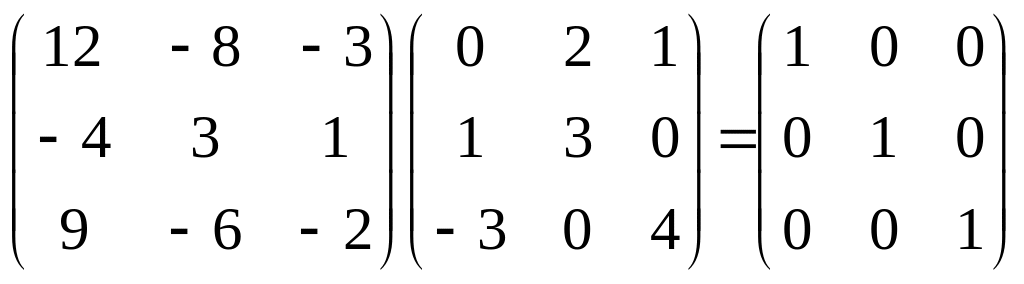
X =

3) Розв’язати рівняння:

AXB=C => XB=A^-1C => X=A^-1CB^-1

1.

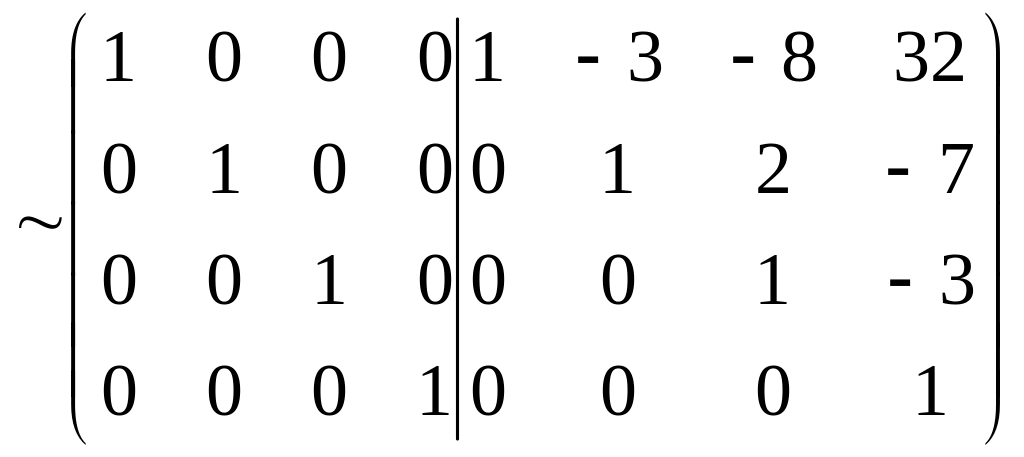A^-1 =

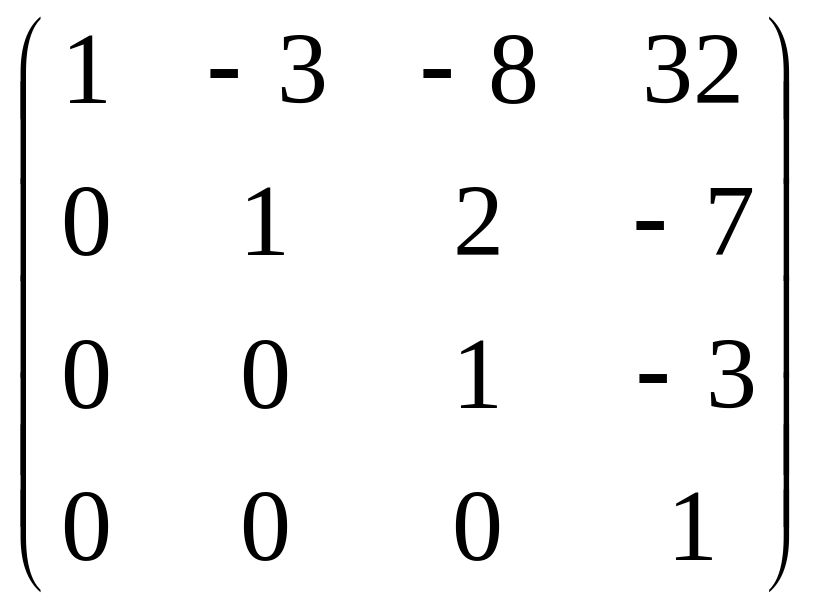
2. A^-1C =

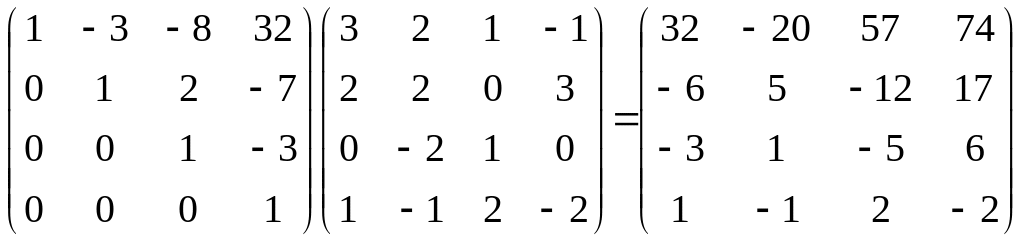
3.

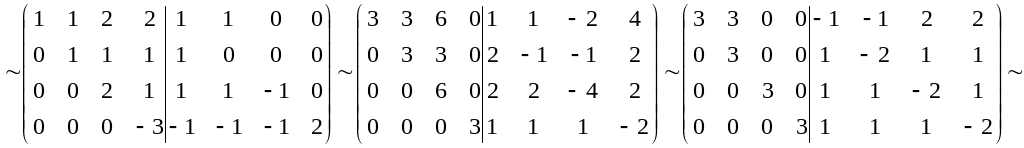
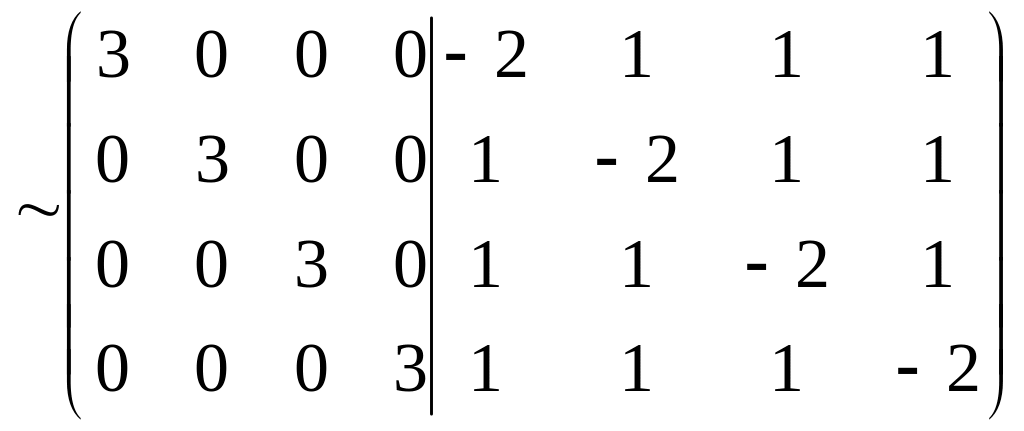
B= -⅓

X= -⅓ 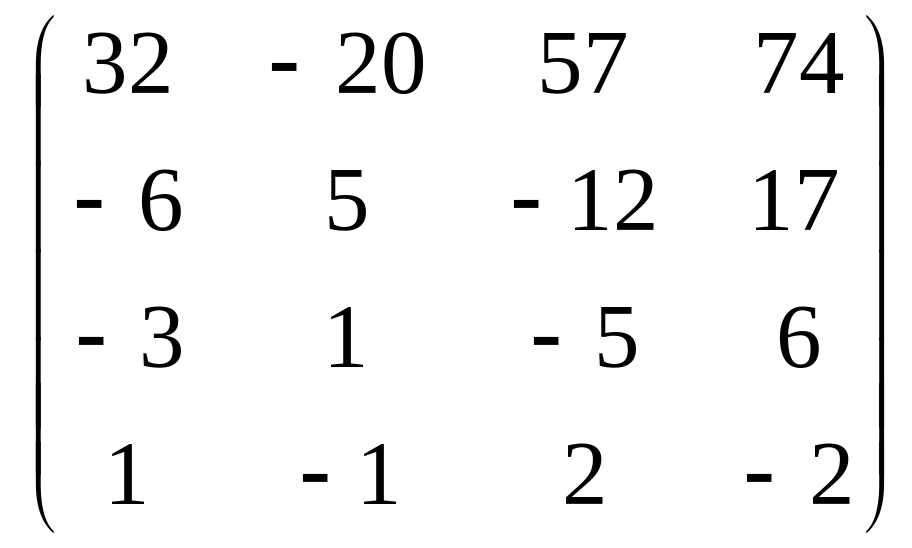= -⅓

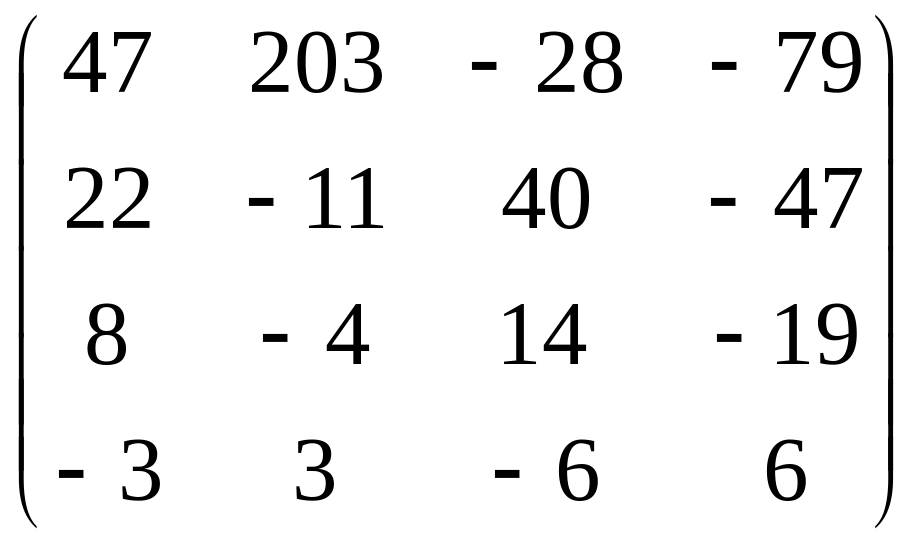
5. Обчислити f(A), якщо

(x+E₃)f(A)=x²-x+2, A=

1. A+E₃ = 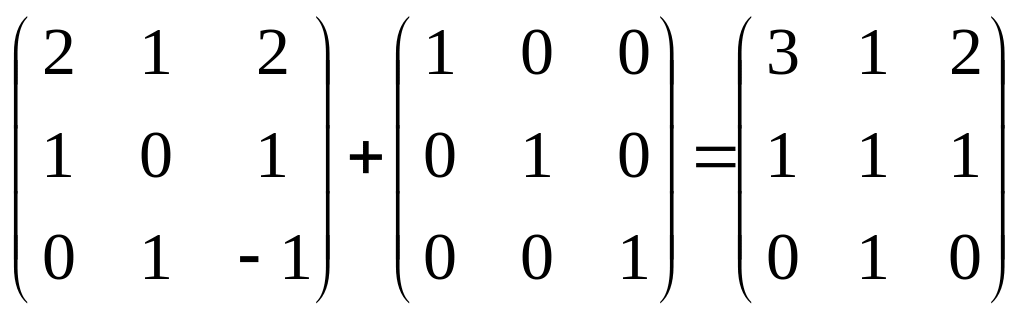= B

Bf(A) = C => f(A) = B^-1C

C = AA-A+2E =

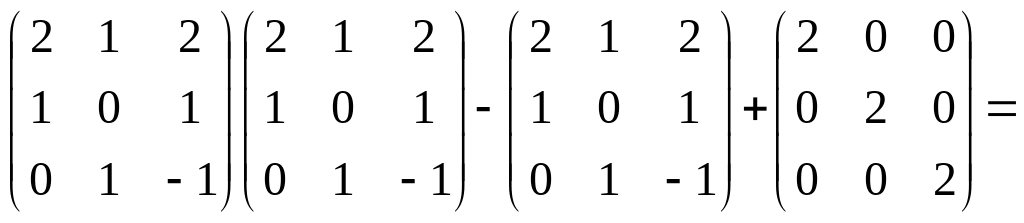
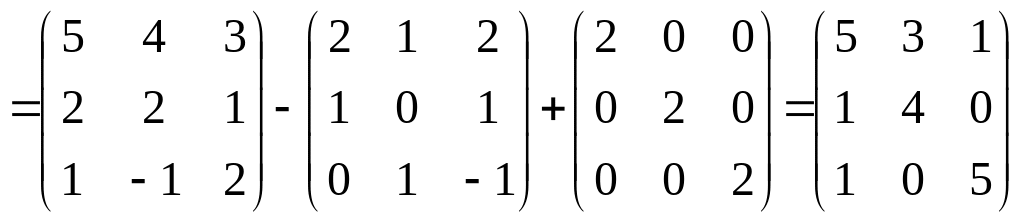
2. Знайдемо B^-1

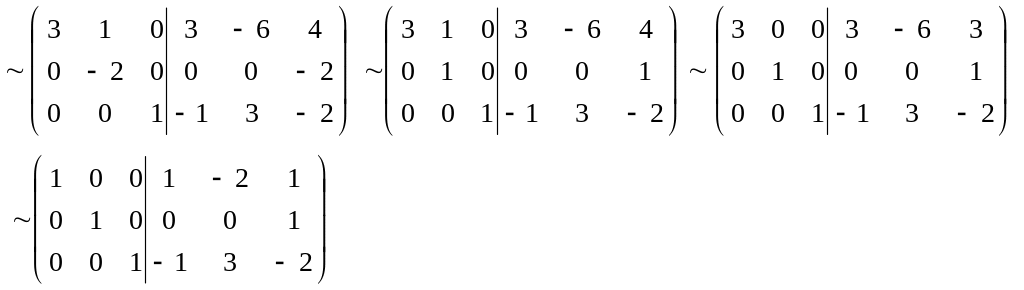
B^-1 =

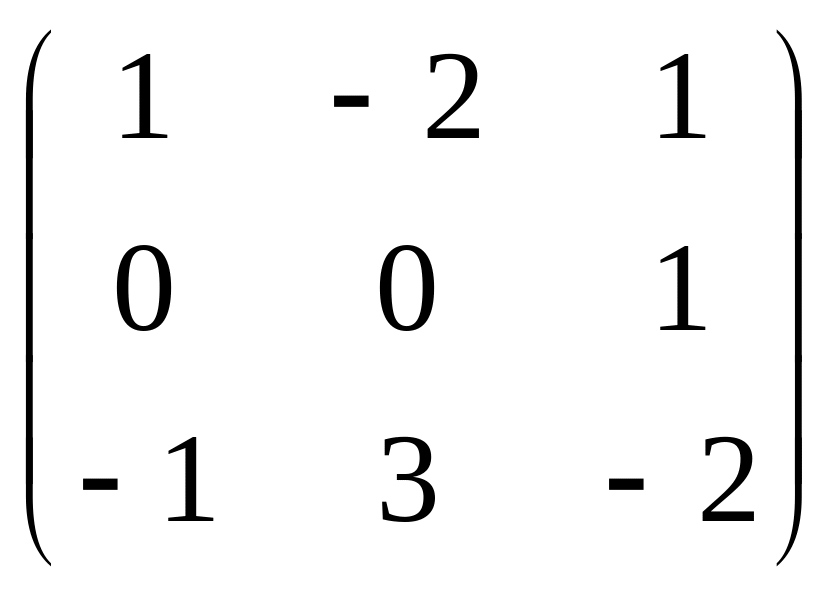
Перевірка :

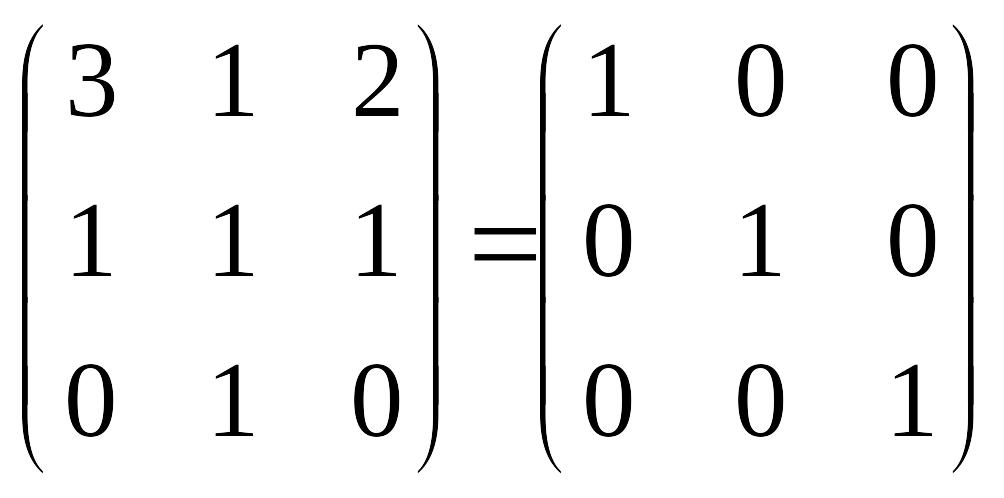
f(A) = B^-1C =

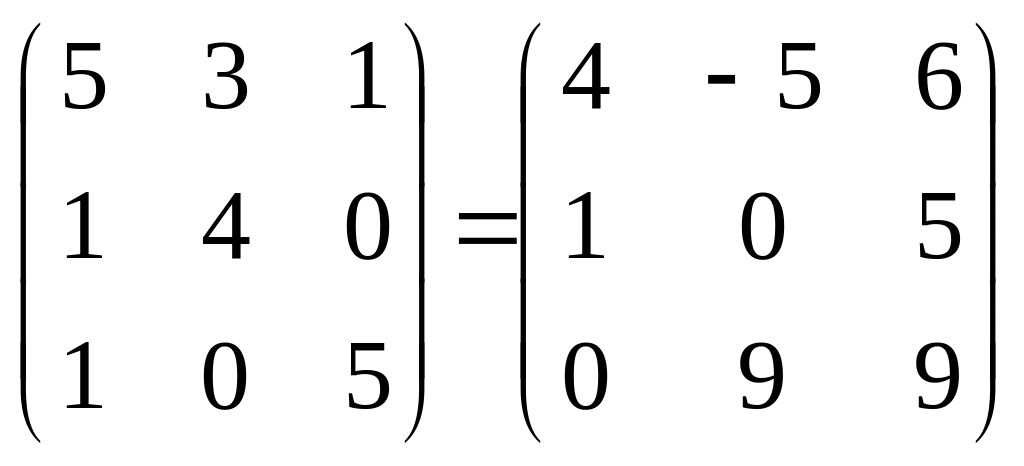
Розділ 3. Визначники. §1. Детермінант (визначник) квадратної матриці. Детермінант другого порядку.

Нехай дана квадратна система лінійних рівнянь з двома невідомими

Розв’яжемо її методом Гауса

1. =a₁₁a₂₂-a₁₂a₂₁0

x₁=( b₁a₂₂-b₂a₁₂)/( a₁₁a₂₂-a₁₂a₂₁)

x₂=( b₂a₁₁-b₁a₂₁)/( a₁₁a₂₂-a₁₂a₂₁)

Число a₁₁a₂₂-a₁₂a₂₁ назвемо детермінантом основної матриці і позначимо

Якщо в детермінанті головної матриці замінити перший (другий) стовпчик стовпчиком вільних членів,

то одержимо відповідно  = і  =

x₁=₁/ x₂=₂/ .

Це є правилом Крамера для розв’язання системи лінійних рівнянь з двома невідомими.

2. = a₁₁a₂₂-a₁₂a₂₁=0  a₁₁/a₂₁=a₁₂/a₂₂.

Тоді система або суперечлива при a₁₁/a₂₁=a₁₂/a₂₂b₁/b₂, або невизначена при a₁₁/a₂₁=a₁₂/a₂₂=b₁/b₂.

Властивості детермінанта другого порядку:

1. Якщо j-й стовпчик матриці А (j=1,2) помножиться на число k, то  також помножиться на k.

2. Якщо j-й стовпчик матриці А (j=1,2) є сумою двох векторів-стовпчиків, то (A)=(A₁)+  (A₂), тобто

3. Якщо в матриці А поміняти місцями два стовпчики, то детермінант поміняє знак.

4. Якщо Е –одинична матриця, то її детермінант дорівнює 1

Означення. Перестановкою з n елементів називається послідовність, утворена внаслідок впорядкування

n-елементної множини.В такому випадку використовуються всі елементи множини.

Різних перестановок можна зробити n!.

Перестановки однакові, якщо відповідні елементи однакові. Зміна місцями двох елементів перестановки називається транспозицією.

Упорядкована пара (i,j) утворює інверсію, якщо i > j.

Наприклад. I=(5 6 3 4 1 2)

Число 5 утворює 4 інверсії, бо (5,4), 5>4, (5,3), 5>3, (5,2), 5>2, (5,1), 5>1.

Число 6 – 4, 3 – 2, 4 – 2, 1 і 2 – жодної.

Отже, G(I)=4+4+2+2=12 – загальна кількість інверсій.

Якщо загальна кількість інверсій парна, то перестановка називається парною, якщо загальна кількість інверсій непарна – перестановка непарна.

Підстановкою з n елементів називається бієктивне відображення

n-елементної множини на себе.

Парність підстановки – сума числа інверсій у верхній і нижній перестановці.

Приклад.

Підстановка K = є парною, бо G(K)=10.

Для обчислення детермінанта третього порядку існує правило “трикутника”.

 = =

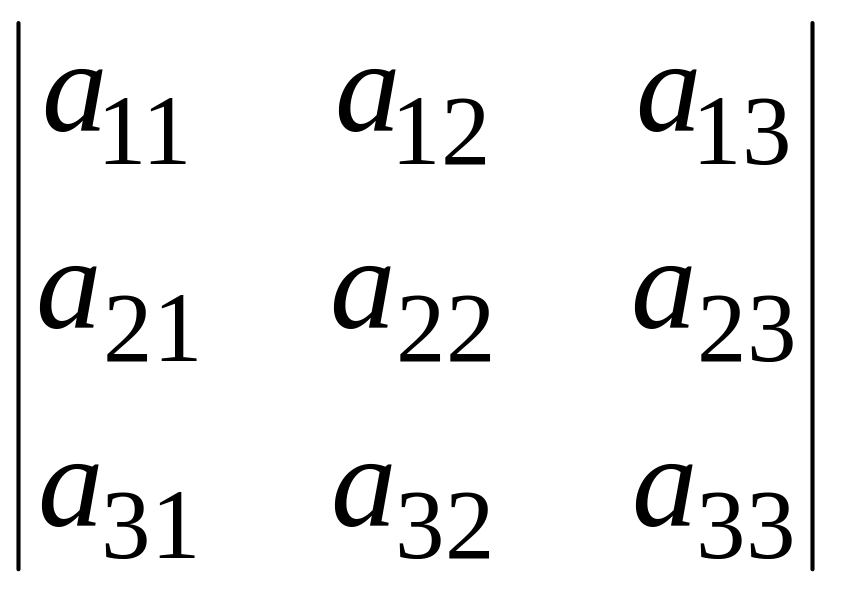= а₁₁a₂₂a₃₃+a₁₂a₂₃a₃₁+a₁₃a₂₁a₃₂-a₁₃a₂₂a₃₁-a₁₂a₂₁a₃₃-a₁₁a₂₃a₃₂

Приклад.

1) Обчислити = = -10+12 = 2

2) Обчислити 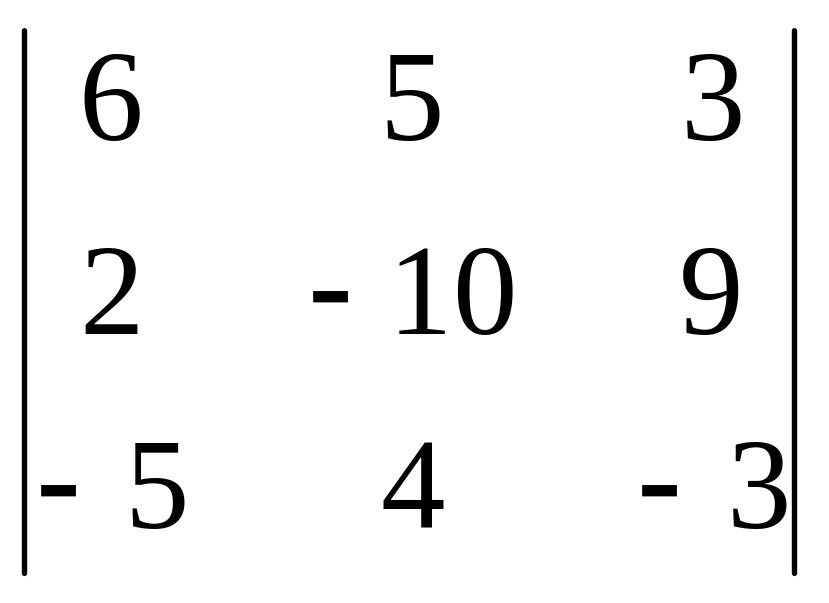 = = 90-225+24-150+30-216=-447