§4. Деякі застосування визначників. Обчислення рангу матриці.

Теорема 1. Для того, щоб детермінант квадратної матриці дорівнював нулю, необхідно і достатньо, щоб ранг цієї матриці був менший її порядку.

Наслідок 1. Детермінант дорівнює нулю тоді і тільки тоді, коли його рядки (стовпці) утворюють лінійно залежну систему векторів.

Наслідок 2. Квадратна матриця є особливою тоді і тільки тоді, коли її детермінант дорівнює нулю.

Наслідок 3. Добуток двох неособливих матриць – неособлива матриця. Добуток двох матриць, хоча б одна з яких особлива, - особлива матриця.

Нехай дана прямокутна матриця А =

Теорема. (про ранг матриці) Для того, щоб ранг матриці дорівнював r, необхідно і достатньо, щоб серед мінорів матриці знайшовся хоча б один мінор r-го порядку, відмінний від нуля, а всі його мінори (r+1)-го порядку дорівнювали нулю.

Означення. Рангом матриці називається найвищий порядок мінорів цієї матриці, відмінних від нуля.

Приклад. Обчислити ранг матриці методом окантування мінорів :

А =

М₁  0

M₂ = = -16+5 = -11

M₃ = = -48-6-45+12+72+15 = 0

M₃ = 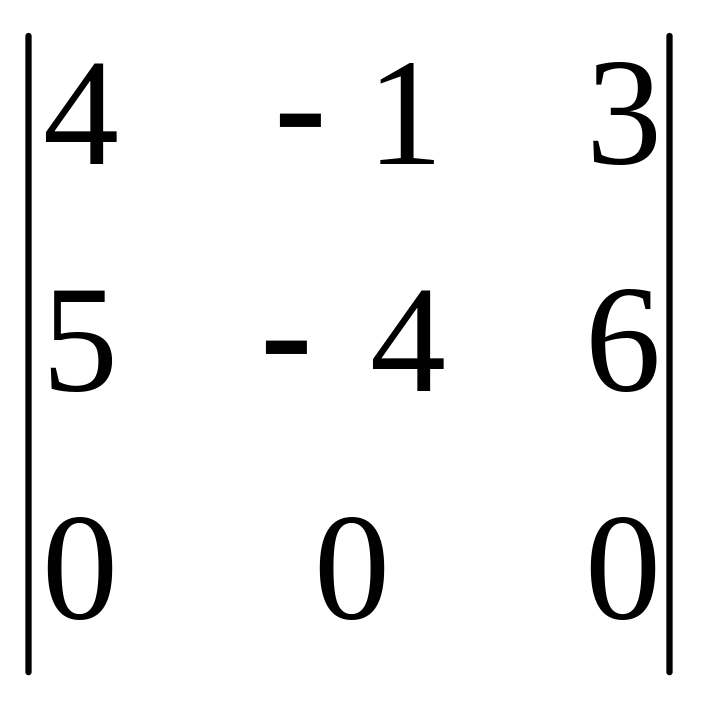= 0

M₃ = = -16-2-15+4+5+24 = 0

M₃ = = 2(-1)⁶ = -22  0

M₄ = = 2 = 0 r(A) = 3

Перевірка :

r(A) = 3

§5. Обчислення оберненої матриці.

Теорема 5. Квадратна матриця має обернену тоді і тільки тоді, коли вона неособлива.

Нехай дана квадратна неособлива матриця А=(а_ij) n-го порядку. Стоїть задача знайти матрицю Х=(х_ij) n-го порядку таку, що АХ=Е, тобто

=

Х = А^-1 =

Для обчислення матриці А^-1, оберненої до матриці А, потрібно замінити кожний елемент а_ij матриці А відповідним алгебраїчним доповненням А_ij, діленим на А, і транспонувати одержану матрицю.

Приклад. Розв’язати матричне рівняння:

Х = XA = B  X = BA^-1

= -4-8+27-6-12-12 = -15

А₁₁ = (-1)² = -2-6 = -8 A₃₁ = (-1)⁴ = -8-6 = -14

A₁₂ = (-1)³ = -(-3-2) = 5 A₃₂=(-1)⁵ = -(4-9) = 5

A₁₃=(-1)⁴ = 9-2 = 7 A₃₃=(-1)⁶ = 4+12 = 16

A₂₁=(-1)³ = -(4-9) = 5

A₂₂=(-1)⁴ = -2-3 = -5

A₂₃=(-1)⁵ = -(6+4) = -10

A^-1 =

Перевірка : = =

X = = =

Розділ 4. Підпростори векторних просторів. §1. Лінійна оболонка системи векторів.

Нехай а₁,а₂,…,а_m – довільна система векторів простору Vn. Утворимо множину лінійних комбінацій векторів системи і позначимо

L(a₁,a₂,…,a_m)={k₁a₁+k₂a₂+…+k_ma_m k_i є Р, i=1,…,m}.

Означення. Лінійна оболонка системи векторів (простір, натягнутий на дану систему векторів) L(a₁,a₂,…,a_m) – це множина всіх лінійних комбінацій векторів даної системи векторів.

Лінійна оболонка замкнута відносно операцій додавання і множення на скаляр. Отже, вона є підпростором векторного простору.

Теорама 1. Розмірність лінійної оболонки даної системи векторів дорівнює рангу цієї системи векторів.

dim L(a₁,a₂,…,a_m)=r(a₁,a₂,…,a_m)

§2. Переріз і сума підпросторів.

Означення. Нехай А,В,С,… - скінченна або нескінченна множина деяких підпросторів простору V. Множина F векторів, які належать одночасно кожному з просторів А,В,С,… називається перерізом цих підпросторів і записують

F=ABC…

Теорема 2. Переріз F будь-якої множини лінійних підпросторів А,В,С,… простору V є лінійним підпростором цього простору.

Означення. Нехай U₁,U₂,…,U_m – скінченна множина деяких підпросторів простору V. Множина U всіх векторів, кожний з яких представимо у вигляді суми u₁+u₂+…+u_m, u_i є U_i, називається сумою підпросторів U₁,U₂,…,U_m і записують U=U₁+U₂+…+U_m.

Теорема 3. Сума скінченного числа лінійних підпросторів U₁,U₂,…,U_m простору V є лінійним підпростором цього простору.

Теорема 4. Розмірність суми двох підпросторів простору V дорівнює сумі розмірностей цих підпросторів мінус розмірність їх перерізу, тобто

dim(U₁+U₂)=dimU₁+dimU₂-dim(U₁U₂).

Приклади.

1. Знайти розмірність суми і розмірність перетину векторних підпросторів U i V, заданих як лінійні оболонки векторів а₁,а₂,…,а_k і b₁,b₂,…,b_m відповідно.

a₁ = (1,2,0,1), а₂ = (1,1,1,0), b₁ = (1,0,1,0), b₂ = (1,3,0,1)

А = r(A)=2

B = r(B)=2

C = r(C)=3

dim(U+V)=3 dim(UV)=2+2-3=1

2. Знайти базиси суми і перетину векторних підпросторів U i V, заданих як лінійні оболонки векторів а₁,а₂,…,а_k і b₁,b₂,…,b_m відповідно.

a₁=(1,2,1,-2), a₂=(2,3,1,0), a₃=(1,2,2,-3), b₁=(1,1,1,1), b₂=(1,0,1,-1), b₃=(1,3,0,-4)

A = r(A)=3

B = r(B)=3

C =

Базис суми {a₁,a₂,a₃,b₂}; dim(UV)=3+3-4=2

Нехай вектор р належить перетину підпросторів, тоді

p=x₁a₁+x₂a₂+x₃a₃=y₁b₁+y₂b₂+y₃b₃

x₁(1,2,1,-2)+x₂(2,3,1,0)+x₃(1,2,2,-3)=y₁(1,1,1,1)+

+y₂(1,0,1,-1)+y₃(1,3,0,-4)

Знаходимо фундаментальну систему розв’язків СЛОР:

X1	X2	X3	Y1	Y2	Y3
-2	1	1	1	0	0
-5	1	-2	0	0	1

p₁=-2a₁+1a₂+1a₃=1b₁+0b₂+0b₃;

p₂=-5a₁+1a₂-2a₃=0b₁+0b₂+1b₃

Вектори р₁ і р₂ є базисом перетину підпросторів.