§2. Алгебраїчне доповнення елемента.

Нехай дана квадратна матриця n-го порядку

A =

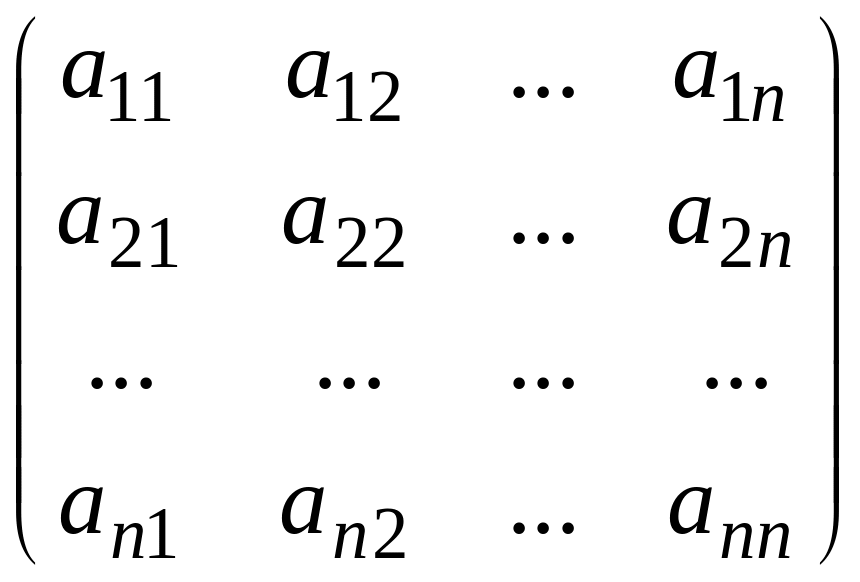
Означення. Мінором (n-1)-го порядку М квадратної матриці А n-го порядку називається детермінант матриці (n-1)-го порядку, який утворений з матриці А викресленням i-го рядка та j-го стовпчика.

Матриця А n-го порядку має n² мінорів (n-1)-го порядку.

Означення. Алгебраїчним доповненням елемента а_ij квадратної матриці А n-го порядку називається мінор М_ij матриці А, помножений на (-1)^i+j, тобто А_ij=(-1)^i+jМ_ij

Приклад 1.

Обчислити всі мінори і алгебраїчні доповнення 2-го порядку визначника

M₁₁ = = -3 M₂₁ = = -1 M₃₁ = = 7

M₁₂ = = -3 M₂₂ = =-1 M₃₂ = = 5

M₁₃ = = -1 M₂₃ = = -1 M₃₃ = = 1

A₁₁ = -3, A₁₂ = 3, A₁₃ = -1,

A₂₁ = 1, A₂₂ = -1, A₂₃ = 1,

A₃₁ = 7, A₃₂ = -5, A₃₃ = 1.

Лема. Детермінант , в якого всі елементи i-го рядка (або j-го стовпця), крім елемента а_ij, дорівнюють нулю, дорівнює добутку елемента а_ij на його алгебраїчне доповнення, тобто =а_ijА_ij.

Теорема. Визначник =а_ij n-го порядку дорівнює сумі всіх попарних добутків елементів будь-якого рядка або стовпця на їх алгебраїчні доповнення, тобто

=а_i1А_i1+…+а_inА_in,

=а_1jА_1j+…+а_jnА_j1

Перша з них – це розклад детермінанта за елементами i-го рядка, друга – розклад детермінанта за елементами j-го стовпця.

Наслідок. Детермінант квадратної матриці n-го порядку дорівнює нулю, якщо всі мінори (n-1)–го порядку дорівнюють нулю.

Теорема. Сума всіх попарних добутків елементів будь-якого рядка (стовпця) визначника на алгебраїчні доповнення відповідних елементів іншого рядка (стовпця) цього визначника дорівнює нулю.

Наслідок. a_1jА_1m+…+а_njА_nm=0 (jm)

a_i1A_k1+…+a_inA_kn=0 (ik).

Приклад 2.

Обчислити детермінант

1 спосіб. Розкладемо детермінант за елементами першого стовпчика

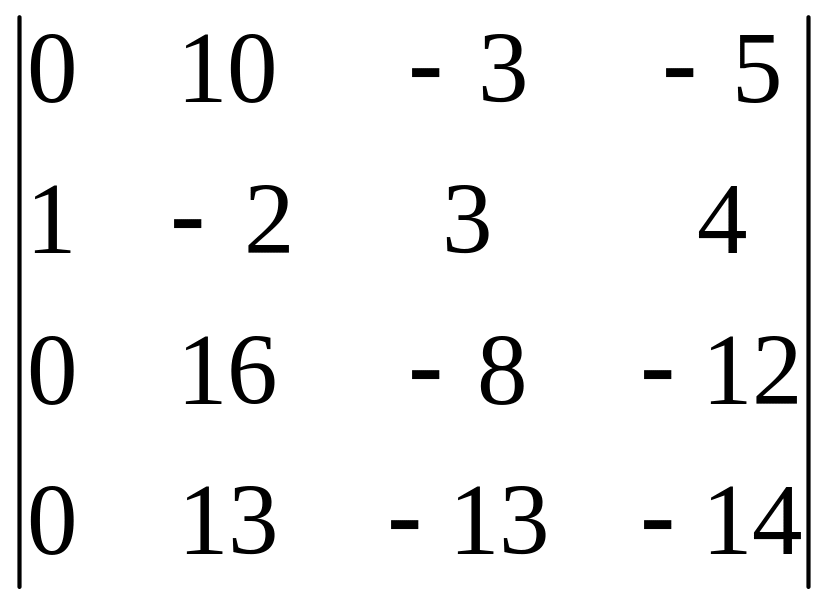= = 3(-1)² + 1(-1)³ +

+ 5(-1)⁴ 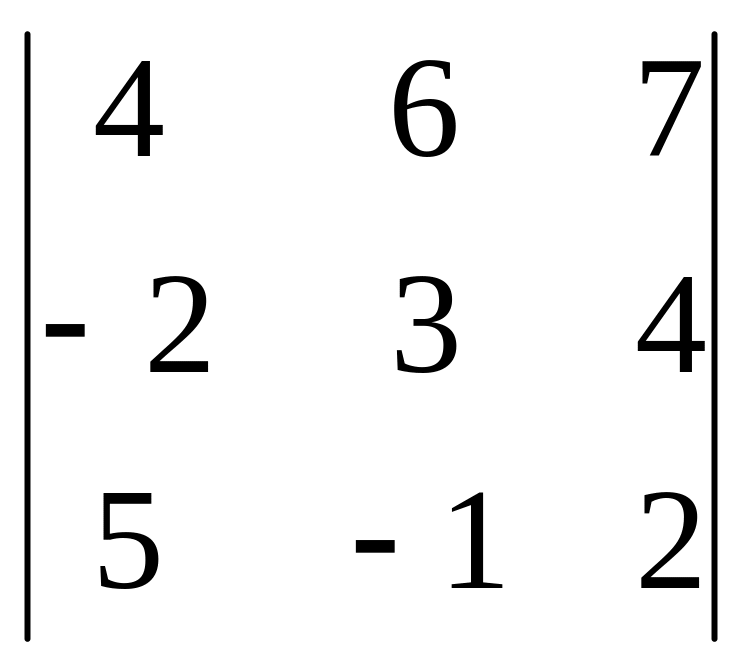+ 4(-1)⁵ =

=3(-28+120-24-140-36-16)-(56+240-42-245-72+32)+5(24+120+14- -105+24+16)-4(96+144-98-126+96-112)=-372+31+465=124.

2 спосіб. За допомогою елемента a₂₁ = 1 обнулимо всі інші елементи першого стовпчика і для обчислення використаємо лему

= = 1(-1)³ =

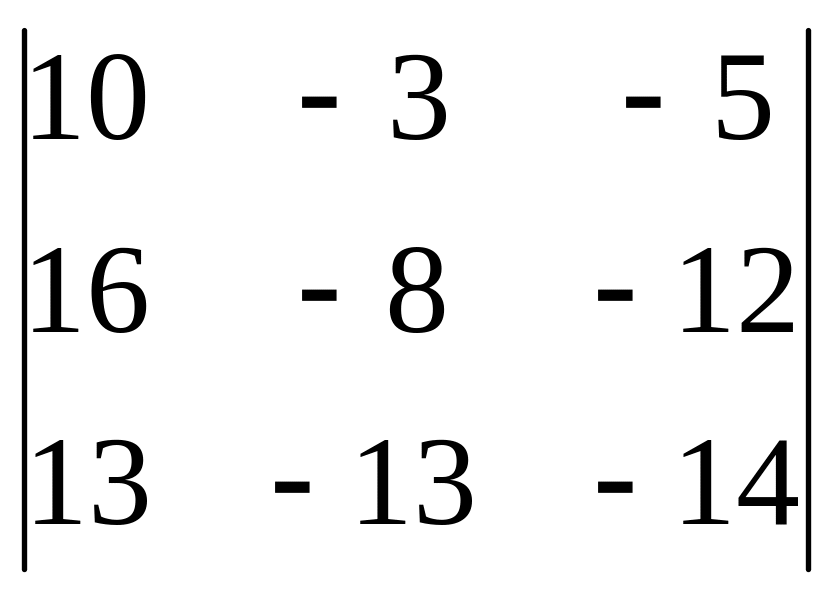= -(1120+468+1040-520--672-1560)=124.

§3. Детермінант n-го порядку.

Означення. Детермінантом n-го порядку квадратної матриці називається алгебраїчна сума n! членів (доданків), кожен з яких є добутком n елементів, взятих з різних рядків і з різних стовпчиків, причому цей добуток береться із знаком плюс, якщо перестановка, утворена з других індексів (при умові, що перші йдуть по порядку), парна, і з протилежним знаком, якщо ця перестановка непарна.

Використовуючи вище сказане, пояснимо знаки доданка а₁₃а₂₁а₃₂ та а₁₂а₂₁а₃₃.

Розташуємо перші індекси по порядку, а з других утворимо перестановку 3,1,2 та 2,1,3 відповідно. Перша перестановка є парною, тому знак доданка а₁₃а₂₁а₃₂ плюс, а друга – непарна, тому знак доданка а₁₂а₂₁а₃₃ – мінус.

Властивості детермінанта n-го порядку :

1. Якщо в детермінанті є нульовий рядок, то детермінант дорівнює нулю.

2. Перестановка рядків (стовпчиків) змінює знак детермінанта.

3. Якщо в детермінанті є два однакові рядки, то детермінант дорівнює нулю.

4. Спільний множник k з одного рядка (стовпчика) можна винести за знак детермінанта.

5. Якщо в детермінанті якийсь рядок є сумою двох рядків, то

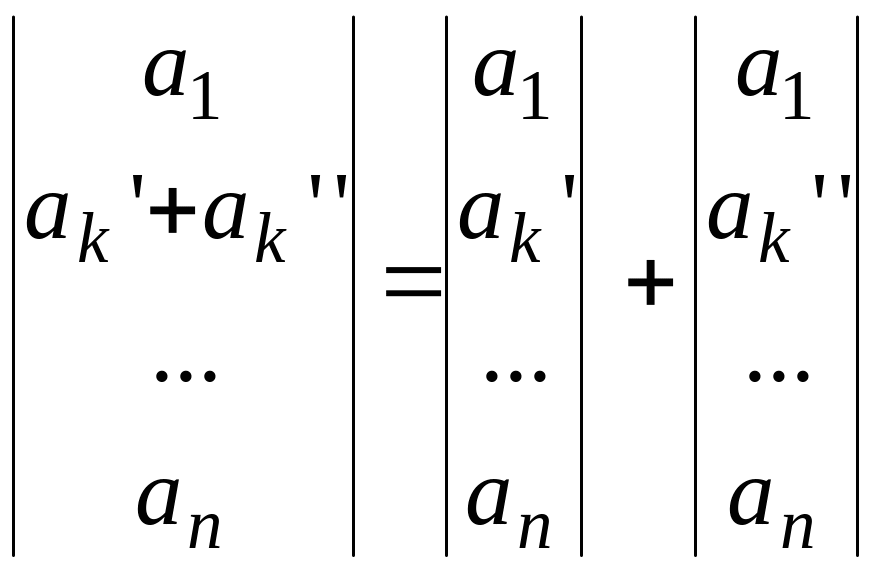
6. Якщо в детермінанті є два пропорційні рядки (стовпчики), то детермінант дорівнює нулю.

7. Якщо в детермінанті k-ий рядок домножити на число р≠0 і додати його до m-го рядка, то детермінант не зміниться.

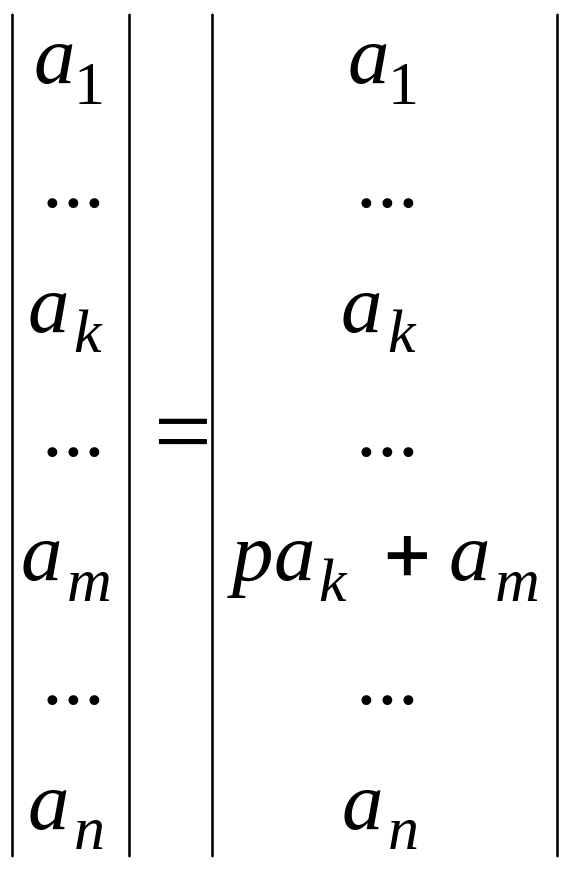
8. Детермінант не змінюється при транспонуванні.

Транспонування – перехід від даного детермінанта до нового, одержаного з даного за таким правилом : всі рядки детермінанта записуються відповідними стовпчиками в новому детермінанті.

9) 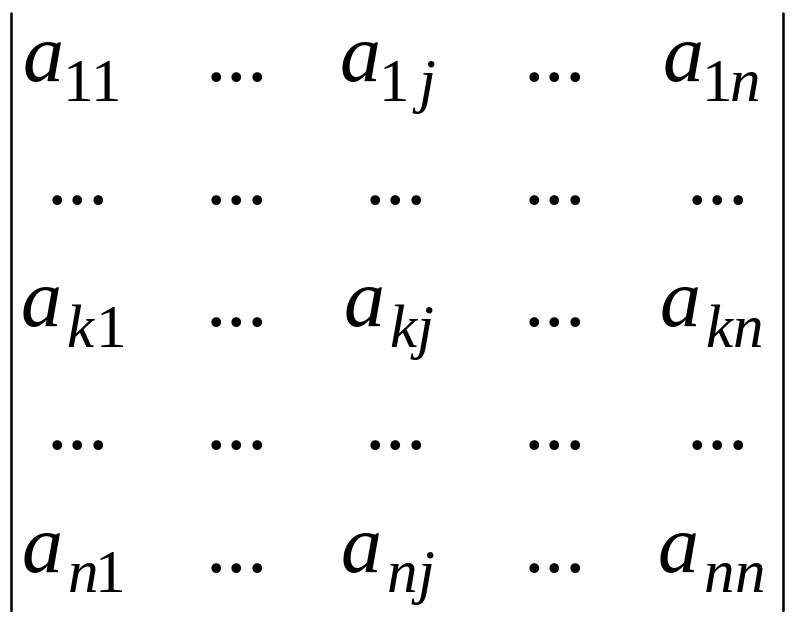=(-1)¹⁺ⁱM_i1a_k1+…+(-1)ⁱ⁺ⁿM_ina_kn = =a_k1A_i1+a_k2A_i2+a_knA_in = 0

Сума добутків елементів рядка на чужі алгебраїчні доповнення дорівнює нулю.

Сума добутків елементів рядка на свої алгебраїчні доповнення дорівнює детермінанту.

Приклад.

1. Розв’язати систему рівнянь методом Крамера:

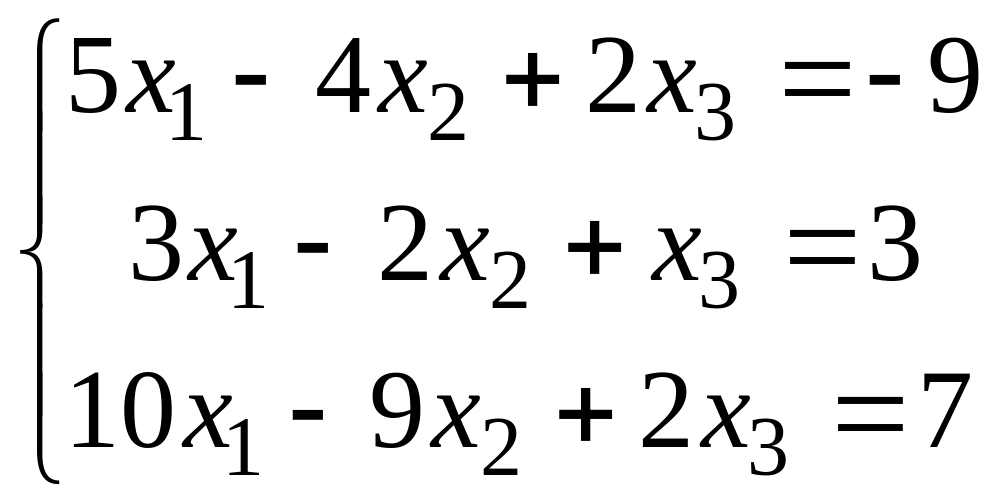
А = 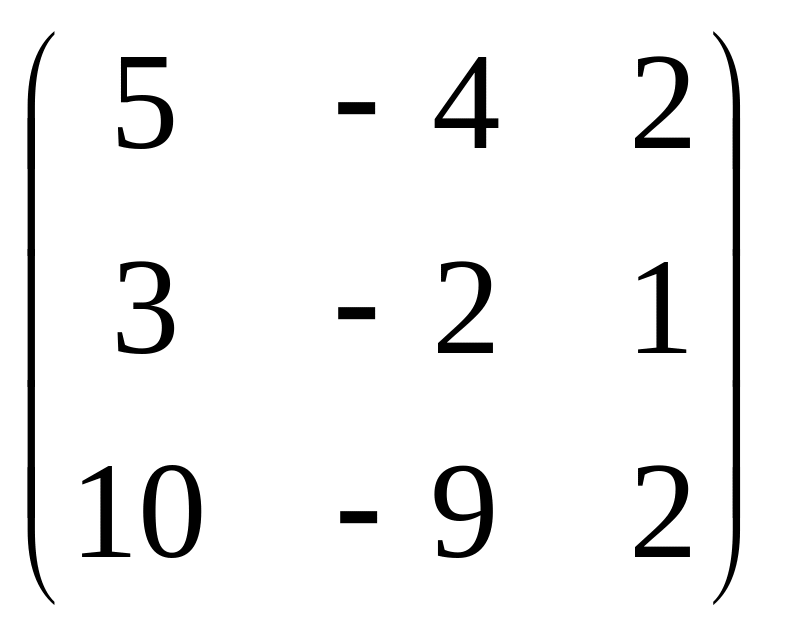В =

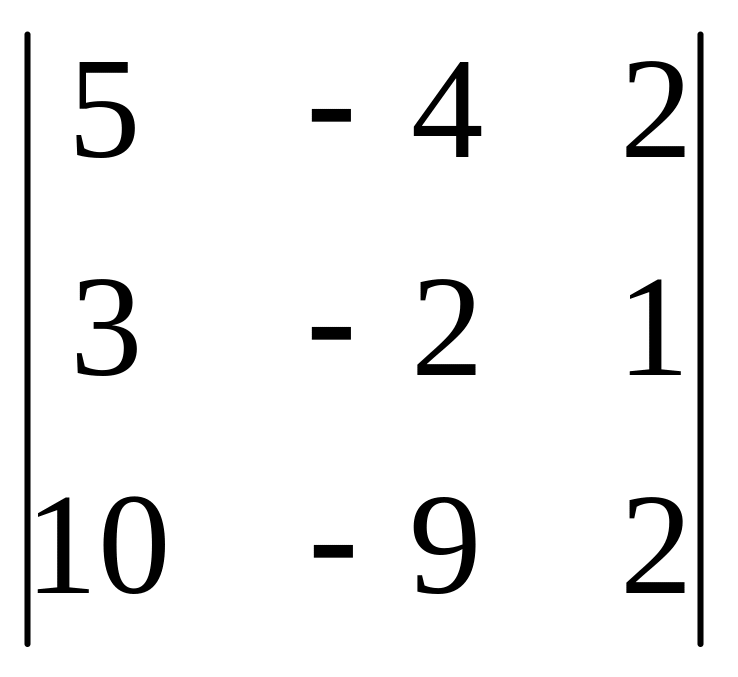 = = -20-40-54+40+24+45 = -5

₁ = = 36-28-54+28-81+24 = -75 х₁ = -75/(-5) = 15

₂ = 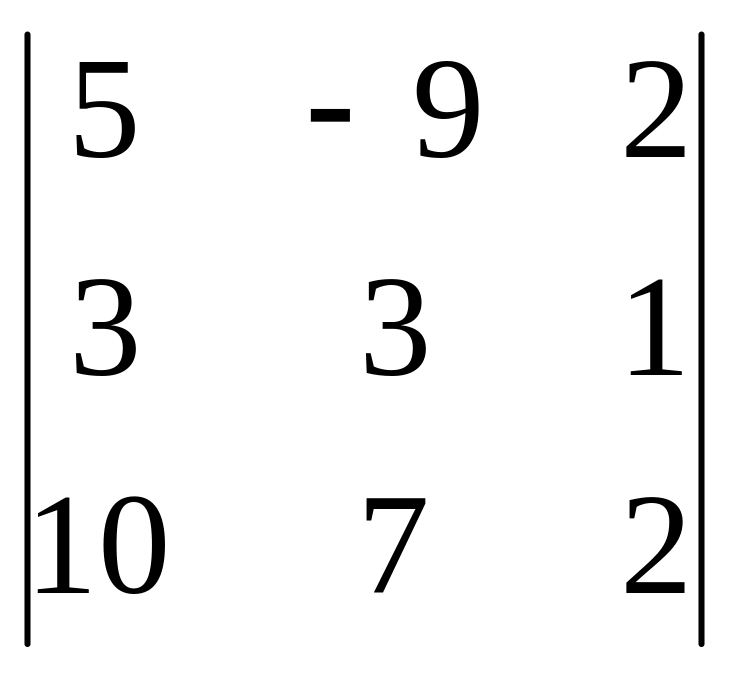= 30-90+42-60+54-35 = -59 x₂ = -59/(-5) = 59/5

₃ = 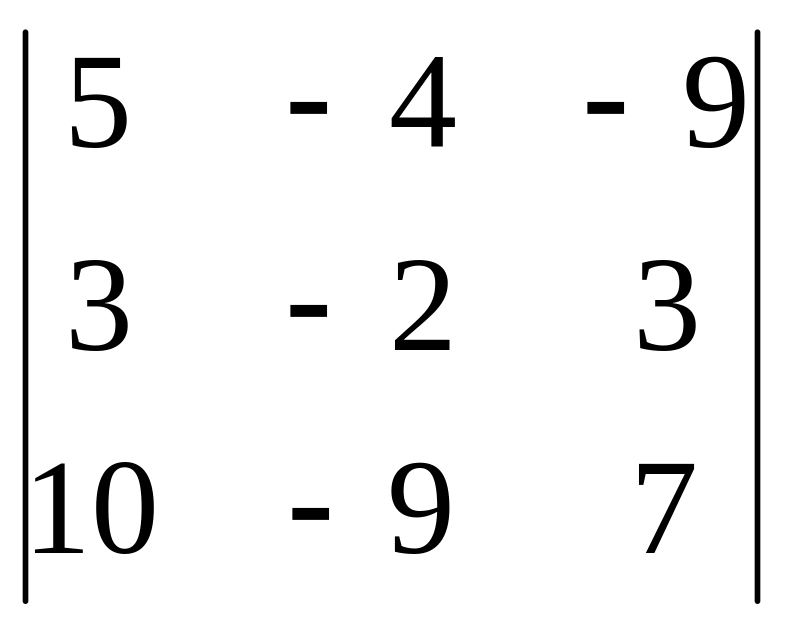= -70+243-120-180+84+135 = 92 x₃ = 92/(-5)= = -92/5

Розв’язок х=(15,59/5,92/5).

2. Розв’язати систему рівнянь методом Крамера:

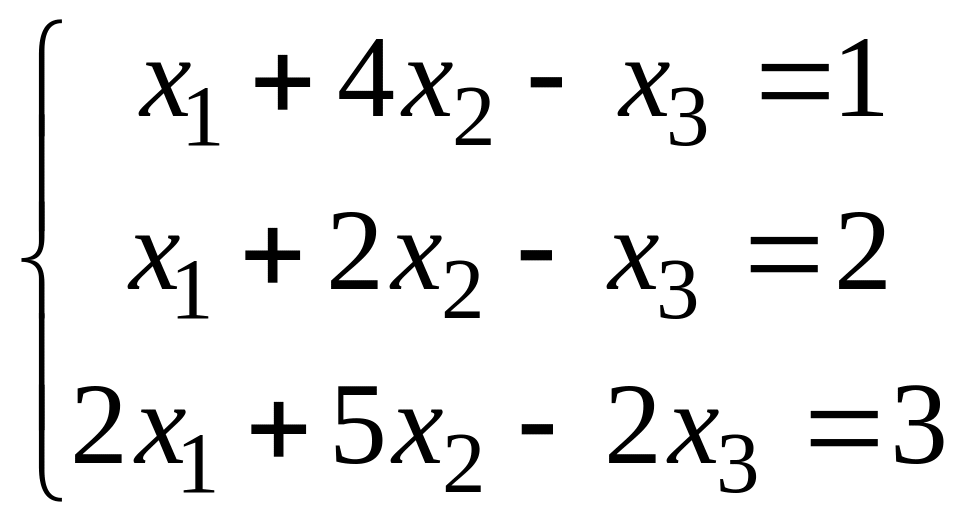
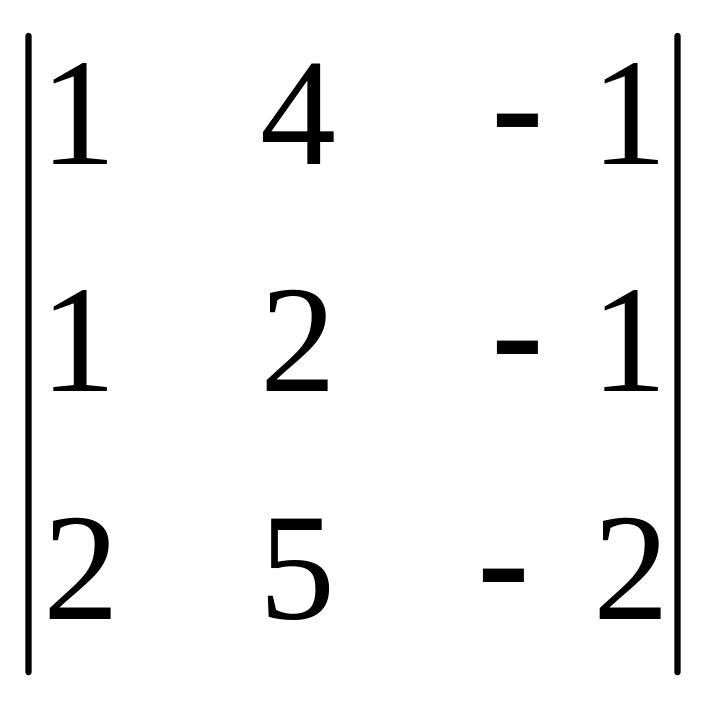 = = -4-8-5+4+8+5 = 0

₁ = 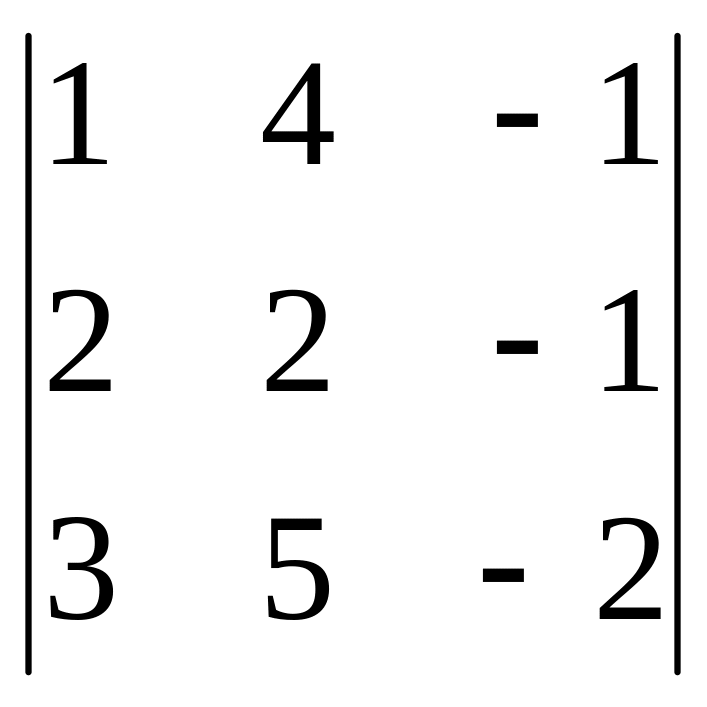= -4-12-10+6+16+5 = 1

₂ = 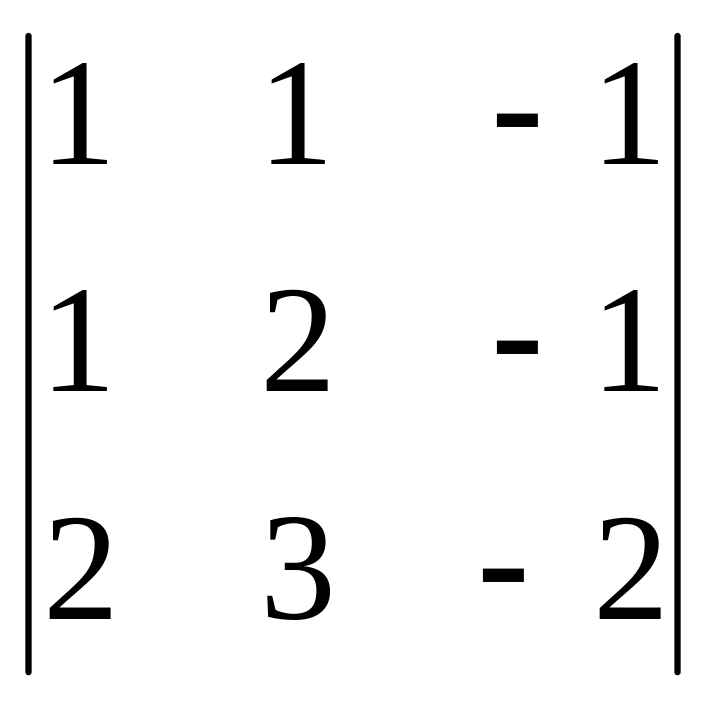= -4-2-3+4+2+3 = 0

₃ = = 6+16+5-4-12-10 = 1

Система несумісна.

3. Розв’язати систему рівнянь методом Крамера:

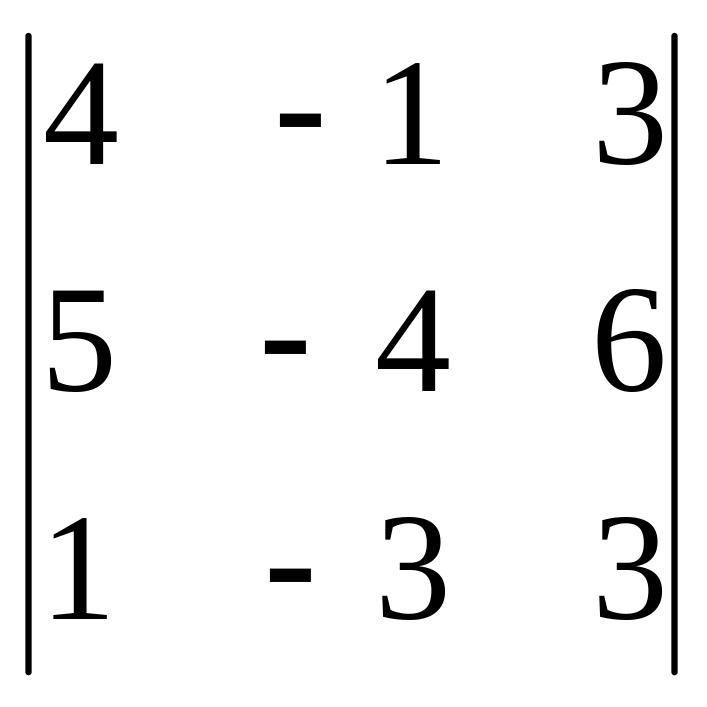 = = -48-6-45+12+15+72 = 0

₁ = = -24-6-27+12+9+36 = 0

₂ = = 36+12+15-9-30-24 = 0

₃ = 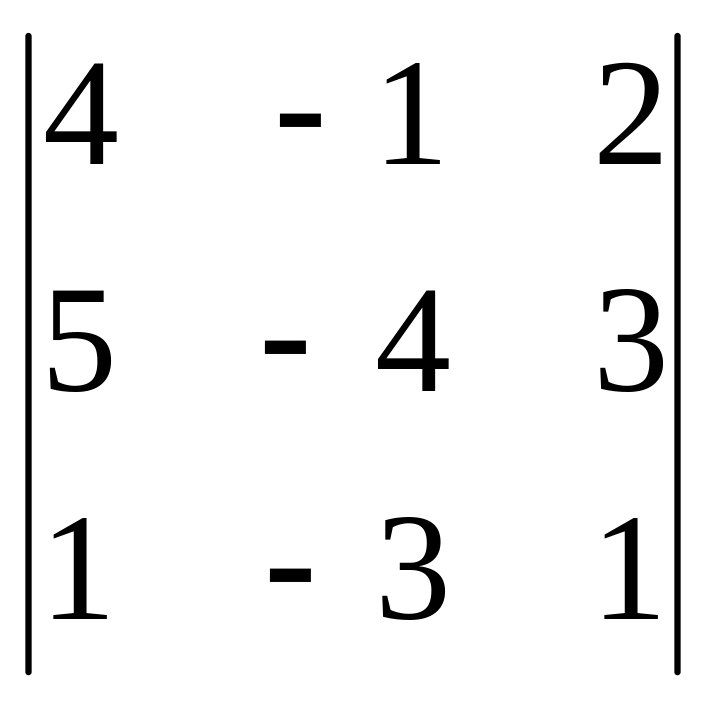= -16-3-30+8+5+36 = 0

Систему методом Крамера розв’язати не можна. Складемо розширену матрицю системи і зведемо її до діагонального виду.

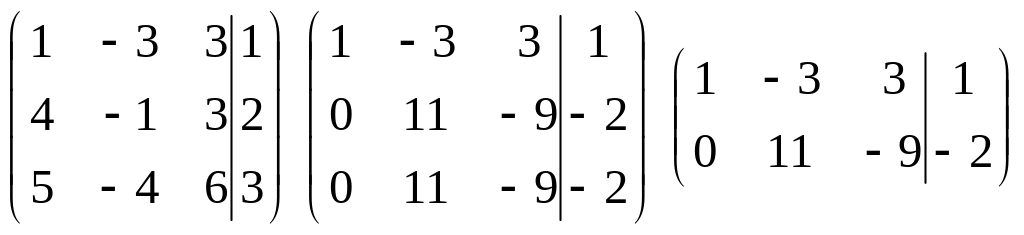
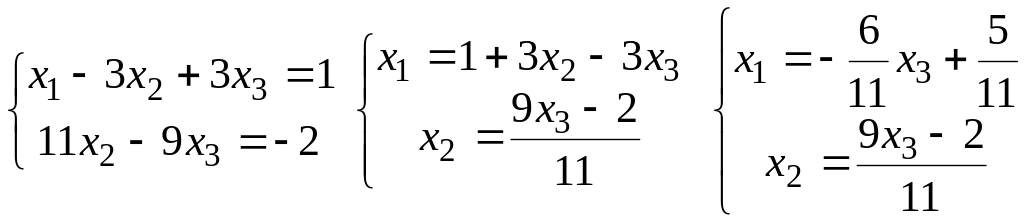
Загальний розв’язок х=( , , x₃), x₃ є R.