2. Интегрирование методом Монте-Карло

Стандартные методы численного интегрирования (методы прямоугольников, трапеций, Симпсона, квадратуры Гаусса. Эти методы, даже если они очень точны для одномерных (обычных) интегралов, быстро обращаются в предельно допустимые при расчетах многомерных (многократных) интегралов, так как необходимое число оценок функции растет весьма быстро, как , где N – число оценок функции, требуемое для вычисления одномерного интеграла, а d – размерность многомерного интерала. В этой ситуации интегрирование методом Монте-Карло, использующее случайные числа, может стать очень удобным.

Независимо от размерности интеграл можно аппроксимировать суммой, в которой функция определяется в случайных точках выражением

Точки х_i случайно и равномерно распределены на [a, b). Так как число точек N растет, центральная предельная теорема (ЦПТ) гарантирует конвергенцию суммы к реальному значению интеграла, причем ошибка имеет порядок .

Вышеупомянутый метод интегрирования, хотя и сходящийся, по-видимому, не очень эффективен, если на данном интервале функция имеет большие осцилляции. Рассмотрим, например, функцию в интервале [0, 1). Разумеется, большое число точек и оценки функции будут «бесполезными» вблизи х=0, где значение функции намного меньше (более чем на 4 порядка), чем для точек вблизи х=1. Выборку чисел на интервале лучше производить неравномерно, чтобы накопить больше точек вблизи х=1 и меньше точек в области, близкой к х=0. Это можно осуществлять выборкой по значимости. Подберем неоднородную функцию распределения Р(х), согласно которой будут выбираться точки хi. Кроме того, можно записать интеграл в следующей форме:

Заметим, что теперь интегрирование функции проводится в точках, распределенных согласно Р. Функция Р, конечно, аналитически известна и нормализована к единице. Флуктуацией будет меньше в подынтегральном выражении , если функция распределения Р, которую можно выбрать по желанию, будет похожа на исходную функцию f.

Основная идея выборки по значимости, по крайней мере в том, чтобы подобрать функцию Р, похожую на f, поэтому функция почти не флуктурирует, и разброс результатов вычислений незначителен. Другими словами, значение интеграла определяется точно даже при относительно небольшом количестве точек.

Формула интегрирования непосредственно обобщается в кратные интегралы

,

где – объем области интегрирования. Например, для двукратного интеграла с прямоугольной области интегрирования имеем

.

3. Приложения метода Монте-Карло к наносистемам, состоящим из нескольких частиц

Вариационный метод Монте-Карло. Подход к интегрированию методом Монте-Карло используется для оценки многомерных интегралов. Это расчет основного энергетического состояния многочастичных систем Е₀

,

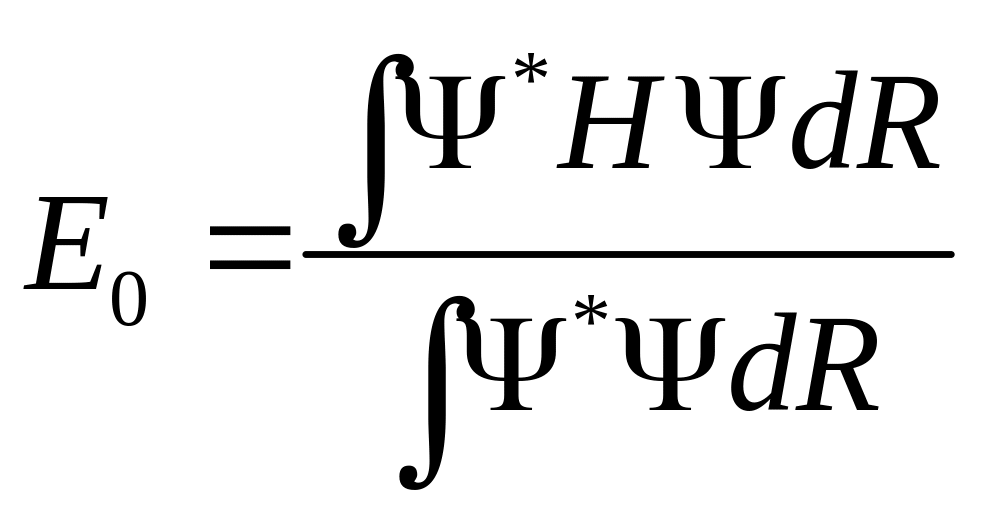как например нескольких электронов в атоме, молекуле или квантовой точке.

В этом уравнении Н – гамильтониан и

(7)

– пробная функция, где коэффициенты ряда нормализованы

Пробная волновая функция содержит ряд вариационных параметров. Интеграл (7) можно переписать через плотность распределения вероятностей волновой функции . Это выражение составляет основу для наиболее точных вычислений свойств квантовых многочастичных систем, находящихся в основном состоянии.

Для расчета функции распределения и средних величин термодинамических свойств нескольких взаимодействующих частиц, заключенных в ограниченном объеме, также можно использовать выборку по значимости

.

Обычный способ проведения выборки по значимости в таких расчетах состоит в генерации рядов случайных точек, распределенных согласно в квантовом случае и в классическом случае.

Затем в первом случае вычисляется среднее значение «локальной энергии»

а в последнем – лишь средняя величина потенциальной энергии . Это лишь отбор, и можно провести выборку точек R в 3-мерном пространстве в соответствии с какой нибудь другой функцией распределения. Как уже говорилось ранее, идея состоит в том, чтобы суммировать функции E(R) или , имеющие самые маленькие из возможных флуктуаций. Следовательно, если флуктуации этих функций все же большие, то можно использовать другую выборку по значимости при условии, что флуктуация распределения аналитически интегрируется так, что вес точек надлежащим образом может быть нормализован.