3. Моделирование наносистем методами Монте-Карло

Моделирование методами Монте-Карло можно использовать в нанонауке для воспроизведения различных сложных физических явлений, включая расчеты величин свойств, предсказания фазовых переходов, самосборку структур, усредненных с помощью термической обработки, распределения зарядов и др. Имеется большое многообразие методов моделирования Монте-Карло, применяемых в зависимости от рассматриваемой наносистемы и желаемых результатов вычислений. Они включают классический, квантовый и объемный методы, но не ограничиваются ими.

Основу моделирования Монте-Карло составляют случайные числа. Для успешного моделирования самая важная проблема – это генерация случайных чисел.

Случайные числа, равномерно распределенные на отрезке [0,1), могут быть сгенерированны с помощью следующего алгоритма:

1. Задается начальное значение чисел_, g, m.

2. S_k = (gS_k-1+ i)mod(m).

3. Для k>0 и 0 S_k<m случайное число r_k = S_k/m.

S₀ называется зерном. При использовании одного и того же зерна может воспроизводиться одинаковый набор чисел. Символы g, i и m обозначают генератор (или множитель), приращение и числовую характеристику. Функция “mod”, на языках С++ и Delphi возвращает остаток (на языке Visual Basic функция 888). Предпочтительно, чтобы S₀ было большим нечетным числом. Число m целесообразно выбирать равным 2^Е, где Е > 35. Большое число g уменьшает корреляции внутри ряда. Число i должно быть простым по отношению к числу m, g –1 многократным по отношению к любому элементарному числу m. Этом случае период последовательности будет равен 2^Е. В языках высокого уровня имеются встроенные функции генерации случайных чисел (Visual Basic и Delphi – “Random”, для инициации генератора случайных чисел имеется функция “Randomize”, которая требуется, чтобы исключить повторяемость набора случайных чисел.).

1. Генерация случайных чисел на отрезке [a, b) в соответствии с заданной функцией распределения p(X)

Выборка по значимости, также известная как «смещенная выборка», может использоваться для генерации случайных чисел согласно заданной функции распределения P(x). Это возможно потому, что эффективность методов выборки по значимости млжет быть заметно увеличена соответствующим отбором точек выборки. Описываемая методика называется «выборкой по значимости».

Назначение выборки по значимости состоит в том, чтобы заострять внимание на точках выборки, где величина функции распределения значительна, и избегать выборки там, где значение функции пренебрежимо мало. Необходимо внести поправку на это смещение точек выборки, взвешивая определенным образом значения выборки. Общий подход к выборке по значимости состоит из двух этапов.

1. На начальном этапе проводится предварительная оценка функции P(x). Интересуемая область делится на довольно крупные ячейки, значение функции P(x) определяется по центру каждой ячейки, и это значение и кумулятивная сумма записываются.

2. Следующий этап состоит в отборе стольких точек выборки, сколько желательно. Но применять методику отбора надо таким образом, чтобы число точек выборки в каждой ячейки было пропорционально значению функции P(x) в центре этой ячейки, опре деленному на этапе (1). При этом каждой выборке задается вес, обратно пропорциональный значению функции в центре ячейки.

Существует несколько способов генерации случайных чисел при помощи выборки по значимости.

1. В случае заданного отрезка [a, b) для получения требуемого числа случайных точек N сначала разделим интервал на 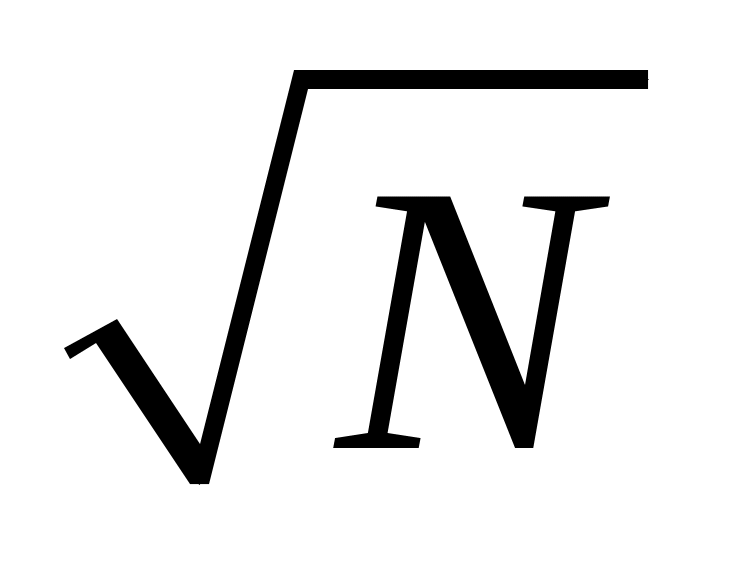частей (это число выбирается произвольно). Далее создадим однородный набор точек для каждой части, при этом число генерированных точек будет равно

где x_i – точка в середине каждой части. Очевидно, что генерированные точки распределяются в соответствии с Р, и их число почти N. Однако следует заметить, что положения точек сильно скоррелированы, и перед использованием требуется их переставить.

2. Однородные случайные числа в интервале [0, 1) отрезка [a, b) можно отобразить аналитически, если функция распределения Р(х) достаточно проста. Если функция распределения вероятностей r в интервале [0, 1) однородна, то имеем

Это соотношение необходимо обратить, если возможно, чтобы получить выражение для х распределятся на отрезке [a, b) в соответствии с Р равномерно.

3. Третий способ состоит в использовании известного алгоритма Метрополиса для произвольно усложненной функции Р. В алгоритме можно начать с произвольной точки в интервале [a, b), например х₀ (a + b)/2, затем добавить к х₀ случайное число, согласно выражению x_i = x₀ +d(2r – 1), где r – случайное число в [0, 1), а d – величина шага. , то шаг принимается; в противном случае это отношение сравнивается со случайным числом в интервале [0, 1). Если данное отношение больше, тогда шаг снова принимается, иначе он отвергается, а старая точка х₀ сохраняется, и начинается другое испытание из этой точки. Имеется также вероятность выхода генерируемых точек из области значений [a, b); в этом случае эти точки отбрасываются. По сравнению с первым алгоритмом этот метод намного менее эффективен, потому что дает много выброшенных точек. Эффективность данного метода очень зависит от выбора размера шага d. При маленьком d большинство испытаний будет принято, но для хорошей выборки потребуется много испытаний. Если же d большой, то можно произвести выборку в [a, b) быстрее, но тогда может быть много выброшенных точек.

4. Более эффективный метод, предложенный Нейманом в 1951 году, состоит из учета при выборе точек функции f {для х на отрезке [a, b); f(x)>P(x)} с использованием представленного выше метода (2) и генерацией точек, распределенных согласно f (рис.1). Наиболее просто было бы принять f постоянной, но большей, чем максимальное Р. Когда такая точка генерируется на отрезке [a, b), случайное число r в интервале [0, 1) сравнивается с отношением Р(х)/f(x). Если r меньше, чем это отношение, то число х принимается, в противном случае оно отвергается, и следует повторить этот процесс с другой точкой х, распределенной согласно функции f. Для постоянной f вероятность принятия х, очевидно, пропорциональна Р(х).

Рис.1. Схема принятия гипотезы в алгоритме фон Неймана для выборки значений двух случайных чисел, распределенных в интервале [0, 1). Первое число преобразованные по методу обратных функций с распределением f, нанесено по координате x , иторое, преобразованное с равномерным распределением, по координате y между 0 и f(x). Если эти числа попадают в область значений под функцией P(x), то точка принимается.