3. Квантовое моделирование нанотранзисторов

Для обеспечения устойчивости решения уравнения Шредингера используется разложение волновой функции электронов в канале по конечному числу поперечных мод.

Аггоритм включает следующие этапы моделирования.

1. Классическое баллистическое моделирование, основанное на самосогласованном решении уравнения Пуассона с функцией распределения Ферми-Дирака.

2. Решение уравнения Шредингера с использованием полученного самосогласованного потенциала для определения коэффициентов прохождения электронов вблизи уровня Ферми в контактах и распределения электронной плотности в канале.

3. Решение уравнения Пуассона с учетом вновь полученной электронной плотности в канале для определения самосогласованного потенциала. Итерирование с этапом 2 до достижения необходимой точности.

4. Вычисление тока согласно выражению Бюттикера-Ландауэра.

Используемый метод стабилизации решения уравнения Шредингера основан на весьма простом приеме. Решение уравнения Шредингера в каждом сечении канала (волновода) раскладывается в суперпозицию конечного поперечных мод, включая и затухающие моды. Далее получаются уравнения для амплитуд этих мод, которые связывают эти моды через соответствующие матричные элементы потенциала в канале. С помощью этих уравнений вычисляются трансфер-матрицы, которые связывают амплитуды мод на входе в канал с амплитудами волн на выходе из канала. Постановка соответствующих граничных условий позволяет определить искомые коэффициенты прохождения. Следует отметить, что убывание матричных элементов потенциала, созданного отдельными примесями в канале, для высших мод позволяет ограничиться их небольшим количеством для решения задачи. Конечно, необходимое их количество может быть установлено в процессе решения. Фактически используется метод, который уже давно широко применяется для расчета распространения электромагнитных волн в неоднородных волноводах.

Точная волновая функция дается решением стационарного уравнения Шредингера

, (2)

где U(x,y,z)=-qφ(x,y,z) – потенциальная энергия в канале, m_x, m_y, m_z – эффективные массы электрона в соответствующих направлениях (рис. 4).

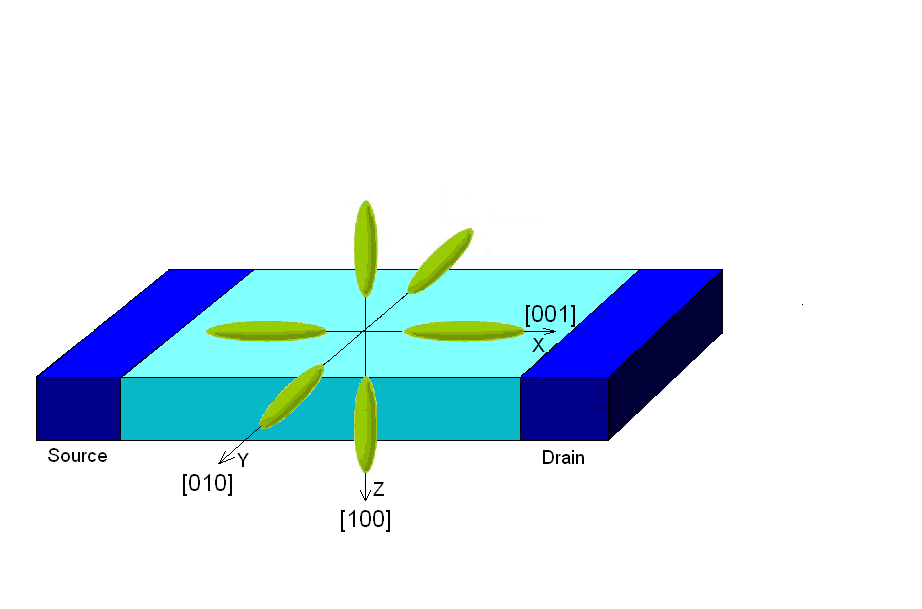
Рис.4 Шесть долин в зоне проводимости кремния при ориентации подложки [100].

Точная волновая функция в каждом поперечном сечении канала (волновода) представляется как суперпозиция всех поперечных мод с соответствующими амплитудами

. (3)

Функции обладают свойством полноты и удовлетворяют двумерному уравнению Шредингера

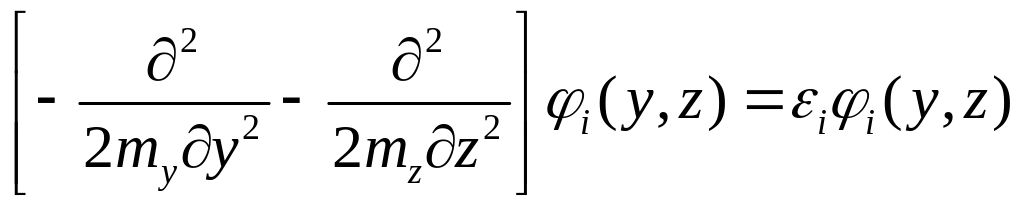. (4)

Предполагается, что функции обращаются в ноль на стенках канала ввиду высокого потенциального барьера на границе раздела Si/SiO₂. Решения уравнения (4) для прямоугольного волновода являются тривиальными

, (5)

, (6)

где W – ширина канала, d – толщина канала, i=(n,m), n и m – целые числа. В этом случае функции являются реальными, ортогональными и нормированными на единицу:

, (7)

где δ_ij – символ Кронекера.

После подстановки разложения (3) в исходное уравнение Шредингера (2), умножения его на и интегрировании его по поперечным координатам y и z получаем уравнения для амплитуд

, (8)

где

(9)

есть матричный элемент потенциала.

Мы оставляет в разложении (3) только конечное число мод. Оправданием такого ограничения является тот факт, что матричные элементы кулоновского потенциала примеси U(r) ~ 1/r для высших мод ( j=(n,m), n >> 1, m >> 1) убывают как

. (10)

Это означает, что трансформацией падающей моды i в высшие моды j можно пренебречь. Уравнения (8) решаются на однородной сетке с узлами в координатах x=x_k, k=-1, 0, 1,...,N, N+1, N+2 и шагом Δx. Конечноразностная аппроксимация системы уравнений (8) есть

. (11)

То же самое в векторной форме

, (12)

где c=(c_i) и ε=(ε_i) - вектора, U=(U_ij) и A=(A_ij) - матрицы. Уравнения (12) можно записать как

, (13)

где I – это единичная матрица. Решение этого уравнения есть

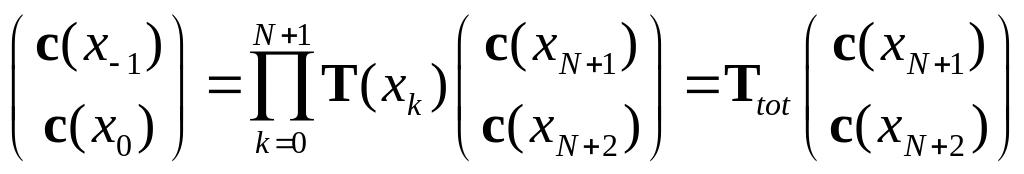. (14)

Это решение связывает амплитуды c на левой границе с амплитудами на правой с помощью полной транфер-матрицы T_tot, которая является произведением трансфер-матриц в промежуточных узлах x_k.

Чтобы поставить граничные условия, необходимо представить амплитуды c в двух крайних точках на левой и правой границах в виде плоских бегущих волн справа налево и слева направо. Естественно, такие условия могут быть поставлены там, где потенциал перестает изменяться в пространстве («выполаживается»), т.е. достаточно глубоко в контактах:

, (15a)

, (15b)

, (15c)

, (15d)

где V_D – потенциал на стоке. Для затухающих мод, которые соответствуют отрицательной продольной энергии необходимо произвести следующую подстановку в уравнения (15b) и (15d):

, (16a)

, (16b)

, (16c)

. (16d)

Для определения коэффициентов прохождения необходимо поставить следующие граничные условия на левом (L) и правом (R) контактах:

для всех и , (17a)

для всех мод, включая . (17b)

В действительности, эти условия означают, что на левую границу падает только волна i-той моды с единичной амплитудой, а на правую границу вообще волны не падают. После подстановки граничных условий (17) в уравнения (15), а затем в уравнение (14) приходим к системе линейных уравнений, из которой и получаем искомые коэффициенты прохождения в виде

. (18)

Эти коэффициенты используются в формуле Бюттикера-Ландауэра для вычисления тока.

На этом расчет еще не заканчивается. Использование выражения (13) позволяет восстановить вид волновой функции электронов в канале, следовательно, вычислить их плотность. Эта плотность будет отличаться от плотности, рассчитанной по классической баллистической модели. Новая (квантовая) плотность подставляется в уравнение Пуассона для корректировки самосогласованного потенциала. Эти итерации продолжаются вплоть до достижения требуемой точности.

Для расчета коэффициентов прохождения для примера выбраны следующие геометрические параметры структуры следующие: длина затвора 10нм, спейсеры по 5нм, толщина кремния 2нм, ширина канала 5нм, эффективная толщина подзатворного окисла 1.5нм. Легирование контактов истока и стока 10²⁰см^-3. Расчетная область включала 5нм контактов, что оказалось достаточным для правильного описания самосогласованного потенциального барьера. Потенциал выполаживался на границах области, что свидетельствовало о том, что достаточная область контактов включена в рассмотрение.

Рассчитанные коэффициенты прохождения для различных долин зоны проводимости кремния при нулевом напряжении на стоке V_D =0 представлены на рисунках 5-7. В отсутствие случайных примесей в канале (рис. 5) коэффициент прохождения резко изменяется от T=0 до T≈1, когда продольная энергия начинает превышать высоту потенциального барьера. Это совершенно соответствует классическому поведению. Небольшие осцилляции коэффициента прохождения, связанные с интерференцией и квантовомеханическим отражением от самосогласованного потенциала, наблюдаются только для электронов из долин [100] и [010] (рис. 5а).

Рисунок 5а. Зависимость коэффициента прохождения от продольной энергии электронов из долин [100] и [010] в канале транзистора. Случайные примеси в канале отсутствуют.

Рисунок 5б. Зависимость коэффициента прохождения от продольной энергии электронов из долин [001] в канале транзистора. Случайные примеси в канале отсутствуют.

Интерференционные пики на зависимостях для 4 и 10 случайных примесей в канале более отчетливы для электронов из долин [100] и [010], чем из долин [001]. Это объясняется значительно меньшей массой продольного движения электронов в канале, следовательно, значительно большей длиной волны.

Следует отметить, что при указанных размерах структуры преимущественно электроны двух долин [100] дают вклад в ток, поскольку именно эти долины имеют наименьшую энергию поперечного квантования в канале.

Казалось бы, что рассчитанное поведение коэффициентов прохождения означает, что ток транзистора с учетом квантового характера продольного движения в канале транзистора может уменьшиться в 1.5-2 раза по сравнению с током, рассчитанным по классической баллистической модели.