2. Интегрирование уравнения движения Ньютона

Для численного интегрирования уравнения движения необходимо дисретизировать время и , используя разложение в ряд Тейлора, записать координаты расположения частиц на последующем временном шаге как функцию текущих координат, скоростей и уравнений, а в некоторых случаях – более высоких производных, следующим образом:

, (4)

.

По существу, это конечно-разностные выражения для координат и скоростей частиц.

Для интегрирования требуются два начальных условия для каждой частицы, так как уравнение движения имеет второй порядок по времени. Обычно начальным координатам и скоростям частиц приписываются определенные фиксируемые значения.

1. Далее с этими начальными значениями можно рассчитать силы, действующие на частицу в момент времени t = 0.

2. Затем, используя вышеприведенное уравнение координаты, которое обрывается после третьего слагаемого, можно получить новое значение координаты.

3. После этого по двум членам уравнения скорости можно получить новое значение скорости.

4. Ускорение, будучи пропорциональным силе, может быть непосредственно рассчитано на каждом шаге, поскольку координаты частицы известны.

Из уравнений (4) мы видим, что при таком обрыве уравнений ошибка в определении v составляет величину порядка а для .

Вследствие «обрыва» уравнений (4) слагаемые с b(t) и более высокого порядка (слагаемые третьего порядка или выше в уравнении координаты и второго порядка или выше в уравнении скорости) не не учитываются и не улулучшают результатов моделирования. Конечно, их можно рассчитать, записав конечно-разностные уравнения для ускорений, но в расчетах не требуются. Для уменьшения ошибки интегрирования по времени, сохраняя при этом шаг как можно большим, необходимы соответствующие алгоритмы.

1. Метод Верле. Сначала координата для предыдущего момента разлагается в степенной ряд в степенной ряд по координате, скорости и ускорению для текущего момента времени t, а затем складываются вместе два уравнения (для моментов и ), чтобы получить выражения для координаты и скорости частицы в момент времени :

, (5)

.

2. Метод с перешагиванием («чехарда»). Здесь скорости частиц рассчитываются в момент времени , т.е. на середине отрезка, соединяющего координаты частиц, тогда как сами координаты и ускорения определяются в моменты, кратные . Это может затруднить начало прогона моделирования. Однако, предполагая, что и , как следует ниже:

, (6)

.

Отметим, что если мы используем периодические граничные условия (как требуется при МД-моделировании макроскопическим путем) и на шаге частица возвращается в рассматривемую область с противопожарной стороны, это не приводит к каким-либо затруднением при моделировании наносистем. Следует также отметить, что в алгоритме Верле мы не получим точных значений скоростей в отличие от алгоритма с перешагиванием. Ошибки метода с перешагиванием – порядка , а СА алгоритм более устойчив, чем в методе Верле.

3. Метод скоростей Верле. Здесь, все координаты, скорости и ускорения частиц рассчитываются в моменты времени, кратные . Сначала, согласно обычным уравнениям движения, обновляются координаты частиц, затем в данных координатах вычисляется ускорение и далее из среднего значения двух ускорений рассчитывается скорость. Данный алгоритм имеет одинаковую точность для нано- и макроскопических систем, так как частицы, покидающие область с периодическими граничными условиями, не вносят каких либо ошибок в расчеты согласно данному алгоритму:

, (7)

.

В СВ- алгоритме требуется определить и сохранять все три переменные (a, v и r). Однако по стабильности этот алгоритм превосходит алгоритм Верле и алгоритм с перешагиванием, потому, что он основываться на неявном численном методе; т.е. скорость в момент времени рассчитывается из ускорения в моменты времени t и . С точки зренмия стабильности, преимущество СВ-алгоритма состоит в том, что он позволяет обновлять координаты с большим по величине шагом и, значит, можно производить более продолжительное время моделирования, используя меньшее число шагов.

4. Предикторно-корректорный метод Гира. Чтобы получать более точные траектории при том же временном шаге или иметь возможность применять большие шаги по времени, можно использовать вычислительный метод более высокого порядка, называемый предикторно-корректорным методом Гира (ПКГ). В этом методе траектории полагаются гладкими функциями времени и используется информация частиц на двух и трех предшествующих шагах времени. В принципе, сначала координаты, затем скорости и, наконец, ускорения предсказываются в момент времени , согласно записанной в конечно-разностной формуле, впрлоть до n-го порядка. Ниже представлены формулы для ПКГ третьего порядка

,

,

. (11)

Лишь после того, как положение частицы будет предсказано можно точно скорректировать ускорение a^K в этот момент. Используя теорию возмущений, можно показать, что ошибка в предсказываемых координатах и скоростях пропорциональна , и, следовательно, с целью достижения максимально возможной точности мв можем внести необходимую поправку при помощи следующих уравнений.

,

,

. (12)

где с₁ = 1, а остальные коэффициенты с целью определения максимальной точности можно определить методом описанным в (Gear C.W. Numerical Initial Value Prolems in Ordinary Differential Eqations. Tngltwood Cliffs. N.J.: Prentice Yfll. 1971 253 p.) В предикторно-корректорном методе третьего порядка с₀ = 0, с₁ = 1, с₂ = 1, а в предикторно-корректорном методе четвертого порядка – с₀ = 1/6, с₁ = 5/6, с₂ = 1/3. Кроме того, могут применяться методы более высокого порядка, но они требуют большего объема компьютерной памяти и могут потреблять больше ресурсов ЦПУ без существенного улучшения точности расчетов.

5. Выбор шага по времени . МД-моделировании важно выбирать шаг по времени ДТ при моделировании микроканонического ансамбля полная энергия системы должна сохраняться. Если величина t будет слишком большой, шаги станут тоже чрезвычайно большими, и частица может войти в область, запрещенную для классического движения, где потенциальная энергия является возрастающей функцией координат. Это может происходить, если сталкиваются две частицы , или частица ударяется о “барьер”,установленный внешним потенциалом. Вхождение в область, запрещенную в классической механике, означает, что новое значение потенциальной энергии стало больше ,чем максимально допустимое. В этом случае полная энергия возрастает и при больших шагах так происходит до тех пор, пока последовательность значений общей энергии не разойдется. Таким образом , в зависимости от соответствующей величины полной энергии приращение t следует выбирать достаточно малым, чтобы значение полной энергии всегда оставалось постоянным, и не слишком маленьким ,чтобы при моделировании не потребовалось чрезвычайно большого количества шагов. Оптимальное значение t обычно находится методом проб и ошибок. Одна фемтосекунда (10^–15c) - хорошая пробная оценка шага , но оптимальное значение реально зависит от начальной энергии и типа рассматриваемого потенциала

3. МД-моделирование систем в контакте с тепловой ванной -термостатом

Система, рассматриваемая при решении широкого класса задач в области физики и химии наносистем, представляет собой закрытую (заданной массой ) систему. К этому типу относится система с фиксированными объемом V и числом частиц N, поддерживаемая при постоянной температуре T. В статистической механике такая система описывается канонически (V,N,T)-ансамблем, где температура выступает в качестве контролирующего параметра.

При моделировании канонического ансамбля его полная энергия не сохраняет своего значения, скорее постоянной во времени остается температура Т, и частицы обмениваются энергией с внешней по отношению к системе тепловой ванной, таким образом ,например кинетическая энергия ,приходящаяся на частицу одноатомного ансамбля ,считается в среднем, равной (3/2)k_БТ. Моделирование при таком характере энергетического обмена или МД-расчет при постоянной температуре можно выполнять самыми разнообразными способами, и ниже мы рассмотрим три из них.

1.Термостат с масштабированием скоростей. Поскольку средняя кинетическая энергия, приходящаяся на моноатомную частицу, равна(3/2)k_БТ, можно просто принудительно задать кинетическую энергию одноатомного ансамбля из N частиц ,постоянно входящих в его состав, равной (3/2)k_БТ. Следовательно ,чтобы приравнять кинетичечкую энергию величине(3/2)k_БТ ,можно умножить все скорости на некий коэффициент пересчета. Это самый простой путь для модельного описания контакта с тепловой ванной при температуре Т. Однако можно показать, что этот способ физически некорректен, поскольку кинетическая энергия-флуктуирующая величина, и лишь средняя энергия одноатомного ансамбля из N частиц равна (3/2)k_БТ.

Теорема равного распределения энергии должна применяться с осторожностью в случае,если произвлдится моделирование жестких многоатомных молекул, обладающих более чем 3 степенями свободы на частицу. Тогда на движение центра масс приходится энергия (3/2)k_БТ, еще (3/2)k_БТ приходится на вращение вокруг центра масс (k_БТ только для двуатомных молекул) в расчете на каждую молекулу. Кинетическую энергию (3/2)k_БТ или (5/2)k_БТ в случае двухатомных молекул следует распределить на все атомы в молекуле. Даже если предположение о жесткости молекулы отсутствует, скорости должны быть пересчитаны так чтобы центр масс имел кинетическую энергию (3/2)k_БТ +(3/2)k_БТ в случае вращения и поступательного движения и ((3/2)(N-2)k_БТ для колебательных (внутренних) степеней свободы движения. Это означает ,что скорости частиц необходимо разлагать на составляющие: скорость движения центра масс и относительную скорость(по отношению к центру). Поэтому кажлая составляющая пересчитывается отдельно, а затем они снова складываются между собой для получения абсолютной скорости частиц.

2. Термостат Hозе-Хувера (метод расширенной системы). Данный метод, генерирующий распределение канонического ансамбля частиц в конфигурационном и импульсном фазовых пространствах, известный под названием метода расширенной системы, предложен Нозе и Хувером. Согласно этому методу, моделируемая система соединяется с тепловой ванной, образуя при этом сложную систему. При таком объединении нарушается условие сохранения энергии системы, которое иначе ограничивает повеление моделируемой системы и приводит к условиям генерации для канонического ансамбля. В сложной флуктуации полной энергии моделируемой системы.

В случае термостата Нозе-Хувера имеется возможность добавления единственной степени свободы, ³, с помощью которой имитируется влияние взаимодействия тепловой ванной с частицами. Лангражиан-частицы также модифицируются с учетом влияния термостата. Можно вывести совместные уравнения, связывающие движение частиц системы и влияние термостата. В данном случае свободная энергия Гельмгольца расширенной системы, включающей частицы вместе с термостатом, сохраняются постоянной. В данном случае уравнения движения имеют следующий вид:

(13)

где f – общее число степеней свободы,  – подбираемый параметр, моделирующий прочность связи системы с термостатом. При малом значении  величина производной  велика и, следовательно, это приводит к большой дополнительной силе трения в уравнениях движения частиц. Параметр  имеет размерность времени, и поэтому к нему можно применить термин «время релаксации». Можно принять величину  примерно 10^–12 с, однако точное значение следует подбирать в зависимости от того, насколько быстрый и глубоко затухающий процесс требуется моделировать. Гамильтониан, на основе которого можно вывести эти уравнения движения, представляется выражением

.

При численном интегрировании модифицированных уравнений движения Ньютона (13) следует подбирать шаг по времени t так, чтобы вышеприведенный гамильтониан сохранял свое значение. Отметим, что если кинетическая энергия, приходящаяся на частицу многоатомного ансамбля, точно равна (3/2)k_bT, тогда  является константой, и можно сначала положить ее равной нулю. Если слагаемое

В гамильтониане положительно, то должно быть также положительным, указывающей на существование силы трения, замедляющей движение частиц. Если это слагаемое имеет отрицательный знак, то должно быть отрицательно, и частицы будут вынуждены далее по направлению импульса так, так чтобы увеличилась их кинетическая энергия. Можно убедиться, что за счет соединения моделируемой системы с тепловой ванной значение кинетической энергии частиц удается удерживать вблизи (3/2)k_bT. Данный термостат можно использовать для моделирования канонического V,N,T – ансамбля.

Если требуется осуществить моделирование N, P, T – ансамбля частиц, находящихся в области переменного объема V(T) при постоянном давлении P₀ то можно, кроме того, добавить дополнительную степень свободы «баростат», связанных с рассматриваемой системой. Тогда результирующие уравнения имеют вид

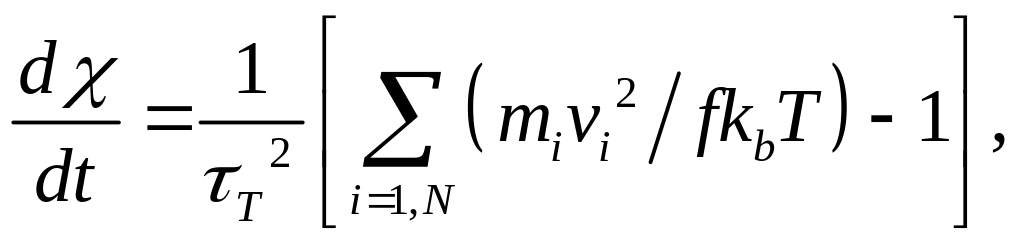(14)

,

где – время релаксации давления, P₀ – заданное давление, R₀ – координата центра масс, и V – объем системы, также рассматриваемый здесь как динамическая переменная. В этом случае свободная энергия Гиббса G, которая определяется выражением

Сохраняет свое значение постоянным. Величины, сохраняющие свое значение, в общем, лучше подходят для контроля стабильности алгоритма обновления и определения важных параметров, например t.

3. Термостат Ланжевена. Третий метод описания обмена энергией между тепловой ванной и частицами состоит в использования термостата Ланжевена.. В этом этом случае траектории движения частиц изменяются под действием двух дополнительных силЖ силы трения и случайной силы, представляющей собой «белый шум» с нулевым математическим ожиданием и среднеквадратичным отклонением 2mk_bT/t в расчете на степень свободы частиц одноатомного ансамбля:

³

.

При реализации этого алгоритма дельта-функцию Дирака в выражении для дисперсии следует заменить на 1/t. Таким образом, на практике необходимо генерировать гауссовское нормальное распределение с нулевым математическим ожиданием и дисперсией, равной 2mk_bT/t для каждого направления силы.

Один из простых способов генерации случайных чисел гауссовского распределения состоит в следующем:

– генерации двух случайных чисел a и b на интервале [0, 1);

– вычислении чисел

и .

Оба числа А и В имеют обычное гауссовское распределение с математическим ожиданием М и дисперсией . В данном термостате  – время релаксации, представляющее собой математическое ожидание времени между столкновениями реальных частиц системы с некоторыми фиктивными (виртуальными) частицами, которые сталкиваются с ними случайным образом и описываются двумя дополнительными силами. Этот термостат интересен тем, что он моделирует физику некоторых стохастических столкновений с виртуальными частицами. Можно показать, что частицы одноатомного ансамбля, следующие этой динамике будут иметь среднюю кинетическую энергию (3/2)k_bT на частицу для трех направлений. Скорость столкновения 1/ моделирует силу взаимодействия с термостатом. Большая величина  означает слабое трение и слабую случайную силу, т.е. слабое взаимодействие с тепловой ванной, поскольку частицы редко сталкиваются с виртуальными частицами ванны. Разумно выбрать значение  приблизительно равным 1000t, но его необходимо подбирать, основываясь на разновидности термического контакта, который моделируется. Для определения этого параметра применяется способ проб и ошибок.

Термостат Ланжевена с малым временем релаксации также интересен при моделировании структурных релаксаций. Действительно, частицы перемещаются в направлении наиболее крутого спуска (т.е. по напралению действия силы F), но, кроме того, им дается некоторый случайный импульс для преодоления возможных потенциальных барьеров. Для релаксации обычно более подходит малое значение . Оно может увеличиваться со временем к концу цикла. Кроме того, к концу циклу можно понизить температуру., точно так же, как это делается в методе моделирования отжига.

МД-моделирование траекторий движения частиц позволяет получить численные значения для ряда функций отклика, включая автокорреляционные функции координат, скоростей или потоков энергий (энергии частиц, умноженные на их скорость), помимо этого можно сделать анимацию частиц в системе, чтобы виртуально наблюдать, каким образом перемещаются сущности на наноуровне.

Применим теорию линейного отклика, можно рассчитать многие свойства молекулярной системы, в том числе структурный фактор, коэффициент диффузии, постоянные упругости, частоты фононов, теплопроводность и, кроме того, равновесные термодинамические свойства (давление.ю внутреннюю энергию, теплоемкость и т.д.). Можно вычислить и количественно предсказать значение вех вышеупомянутых физических свойств.

Другое важное применение МД-моделирования – это определение структуры молекул и кластеров в основных состояниях. В настоящее время это делается на очень больших органических молекулах.