10.2. Методы Рунге-Кутты.

Для уменьшения погрешности метода интегрирования ОДУ, использующего разложение искомого решения в ряд Тейлора (6.6), необходимо учитывать большее количество членов ряда Однако при этом возникает необходимость аппроксимации производных от правых частей ОДУ. Основная идея методов Рунге-Кутты заключается в том, что производные аппроксимируются через значения функции f(x, у) в точках внутри интервала [х₀, х_{0 + h}], которые выбираются из условия наибольшей близости алгоритма к ряду Тейлора. В зависимости от старшей степени h, с которой учитываются члены ряда, построены вычислительные схемы Рунге-Кутты разных порядков точности.

Наибольшую популярность получил метод Рунге-Кутты 4-го порядка. Вычислительные формулы этого метода имеют такой вид:

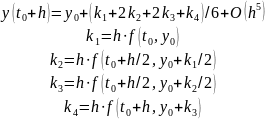
Эта вычислительная схема требует вычисления правых частей ОДУ в четырех точках.

10.2.1. Метод Рунге-Кутты-Мерсона

Мерсон предложил модификацию метода Рунге-Кутты четвертого порядка, позволяющую оценивать погрешность на каждом шаге и принимать решение об изменении шага.

Схема Мерсона требует на каждом шаге вычислять правую часть ОДУ в пяти точках, но за счет только одного дополнительного коэффициента по cравнению с классической схемой Рунге-Кутты на каждом шаге можно определить погрешность решения R.

Если погрешность велика, то полученное решение отбрасывается, а шаг интегрирования уменьшается в два раза, если значение погрешности меньше порогового, то шаг интегрирования увеличивается в два раза.

Автоматический выбор шага позволяет значительно сократить время решения ОДУ. При автоматическом выборе шага интегрирования иногда возникает необходимость вывода (использования) результатов только в фиксированных точках. Также возникает опасность очень сильного дробления шага интегрирования на отдельных участках.

10.3. Метод Адамса.

При решении задачи Коши методами Рунге-Кутты необходимо вычислять правые части ОДУ в нескольких точках на каждом шаге. Количество точек Зависит от порядка используемого метода После того как искомая интегральная кривая у(х) определена в нескольких точках х₀, х₁,..., х_п, можно применить алгоритмы интерполяции и сократить количество вычислений правых частей ОДУ для получения решения в очередной точке х_п+1. Подобные методы называют многоточечными, или многошаговыми.

При анализе четырех известных точек интегральной кривой с помощью интерполяционного полинома Ньютона, получим экстраполяционную формулу Адамса:

(10.5)

Значительная величина коэффициента в остаточном члене обусловлена тем, да точка х₄ лежит вне интервала расположения узлов [х₀, х₃], по значениям функции f(x),в которых построен интерполяционный полином. То есть мы имеем дело с экстраполяцией, погрешность которой всегда больше, чем при интерполяции.

С целью уменьшения погрешности способом, аналогичным получению формулы (10.5), по узлам x_l, х₂, х₃, х₄ строится интерполяционная формула Адамса

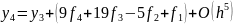(10.6)

Последняя формула является неявной, так как искомая величина у₄ необходима для вычисления значения функции f₄ = f(x₄, у₄), входящего в правую часть. Выражение (10.6) можно рассматривать как нелинейное уравнение относительно неизвестной величины у₄ и решать его одним из численных методов. Наиболее часто здесь используется метод простых итераций, хотя в некоторых случаях оказывается более предпочтительным метод Ньютона. Следует иметь в виду, что каждая итерация потребует нового вычисления правой части дифференциального уравнения f(x, у).

Решение, определенное по экстраполяционной формуле (10.5), обычно выбирается в качестве начального приближения для итерационных методов. Поэтому выражение (10.5) рассматривается как формула прогноза, тогда выражение (10.6) является формулой коррекции.