8.3. Метод хорд.

Рассматриваемый метод так же, как и метод дихотомии, предназначен для уточнения корня на интервале [а, и], на концах которого левая часть решаемого уравнения f(x) принимает резные знаки.

Очередное приближение теперь в отличие от метода дихотомии берем не в середине отрезка, а в точке x_l где пересекает ось абсцисс прямая линия, проведенная через точки f(a) и f(b) (рис. 8.2).

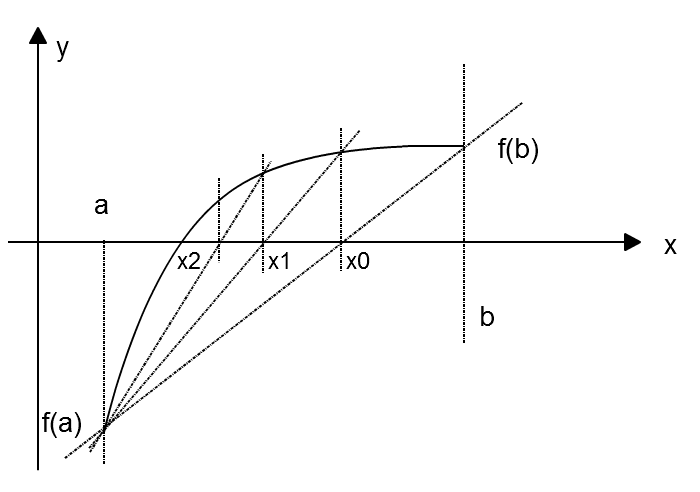
Рисунок 8.2 – Пояснение к решению нелинейного уравнения методом хорд.

Уравнение прямой линии, проходящей через точки f₁= f(a) и f₂ = f(b), запишем в общем виде

у(х) = kх + с.

Коэффициенты к и с уравнения этой прямой определим из условий

f₁ = kа + с; f₂ = kb + с.

Вычитал левые и правые части последних соотношений, получим

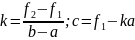
Точку пересечения прямой у(х) с осью абсцисс получим, приравнивая у(х) нулю

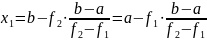
В зависимости от знака функции в уточненной точке x₁ на основании теоремы Больцано-Коши уточняем, какой отрезок будет использован для следующего шага поиска.

Процесс поиска корня останавливается тогда, когда расстояние между очередными приближениями станет меньше заданной погрешности ε:

Дискуссионный вопрос. Предположим, что график заданной функции хотя и имеет единственный корень, но имеет особенность: он очень медленно изменяется в районе нуля. Какие проблемы возникнут при использовании метода секущих или метода половинного деления, при отыскании корня подобной функции?

8.4. Метод касательных (метод Ньютона-Рафсона).

Рассмотрим графическую иллюстрацию метода (рис. 8.3).

П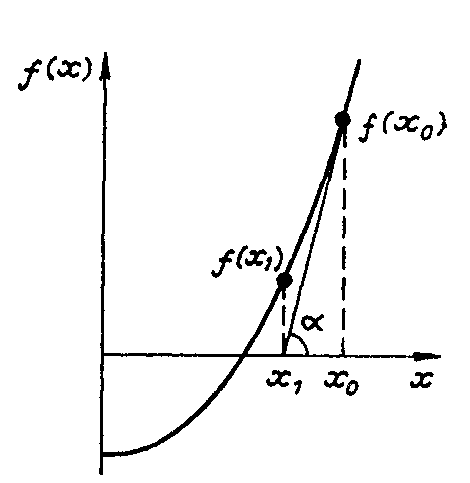 редположим, что графическим методом определено начальное приближение х₀ к корню. В точке х₀ вычислим левую часть решаемого уравнения f₀ = f(x₀), а также производную в этой точке f'(x₀) = tg α. Следующее приближение к корню найдем в точке x_l, где касательная к функции f(x), проведенная из точки (X₀, f₀), пересекает ось абсцисс. Затем считаем точку х₁ в качестве начальной и продолжаем итерационный процесс. Из рис. 8.3 видно, что таким способом можно приближаться к корню х*. При этом с каждой итерацией расстояние между очередным х_к+1 и предыдущим х_к приближениями к корню будет уменьшаться. Процесс уточнения корня закончим, когда выполнится условие

|x_{k + 1}- х_k| < ε

где ε - допустимая погрешность определения корня.

Из геометрических соотношений рис. 8.3 получим основную формулу метода Ньютона

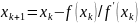
Метод Ньютона обладает высокой скоростью сходимости. Обычно абсолютная точность решения 10^-5 - 10^-6 достигается через 5-6 итераций.

Недостатком метода является необходимость вычисления на каждой итерации не только левой части уравнения, но и ее производной.

Можно, несколько уменьшив скорость сходимости, ограничиться вычислением производной f'(x) только на первой итерации, а затем вычислять лишь значения f(x), не изменяя производной f'(x). Это алгоритм так называемого модифицированного метода Ньютона.

Лекция 9. Численное интегрирование и дифференцирование.

Ставится задана вычислить интеграл вида

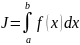(9.1)

где а и b - нижний и верхний пределы интегрирования; f(x) – непрерывная функция на отрезке [а, b].

К численному интегрированию обращаются тогда, когда нельзя через элементарные функции аналитически записать первообразную интеграла (9.1) или когда подобная запись имеет сложный вид.

Сущность большинства методов вычисления определенных интегралов состоит в замене подынтегральной функции f(x) аппроксимирующей функцией φ(x), для которой можно легко записать первообразную в элементарных функциях, т.е.

где S - приближенное значение интеграла; R - погрешность вычисления интеграла

Используемые на практике методы численного интегрирования можно сгруппировать в зависимости от способа аппроксимации подынтегральной функции. Дадим краткую характеристику групп наиболее распространенных методов.

Методы Ньютона-Котеса основаны на полиномиальной аппроксимации подынтегральной функции. Методы этого класса отличаются друг от друга степенью используемого полинома, от которой зависит количество узлов, где необходимо вычислить функцию f(x). Алгоритмы методов просты и легко поддаются программной реализации.

Сплайновые методы базируются на аппроксимации подынтегральной функции сплайнами, представляющими собой кусочный полином. Методы различаются по типу выбранных сплайнов. Такие методы имеет смысл использовать в задачах, где алгоритмы сплайновой аппроксимации применяются для обработки данных.

В методах наивысшей алгебраической точности (методы Гаусса-Кристоффеля и другие) используются неравноотстоящие узлы, расположенные по алгоритму, обеспечивающему минимальную погрешность интегрирования для наиболее сложных функций при заданном количестве узлов. Методы различаются способами выбора узлов и широко используются для интегрирования, в том числе они применимы и для несобственных интегралов. Хотя из-за необходимости хранения числовых констант и стандартизации пределов интегрирования программы указанных методов требуют несколько большего объема памяти по сравнению с методами Ньютона-Котеса.

В класс специальных группируются методы, алгоритмы которых разрабатываются на основе учета особенностей конкретных подынтегральных функций, что позволяет существенно сократить время и уменьшить погрешность вычисления интегралов.