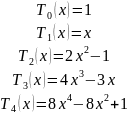5.1. Степенной базис

Выберем базисные функции φ_k(х) в виде последовательности степеней аргумента х, которые линейно независимы,

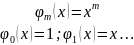(5.4)

В этом случае так же, как и при интерполяции, мы будем аппроксимировать экспериментальную зависимость полиномом. Однако степень полинома n выбираем обычно m<<n (при лагранжевой интерполяции m=n).

Аппроксимирующая кривая в МНК не проходит через значения исходной функции в узлах, но проведена из условия наименьшего суммарного квадратичного отклонения. Экспериментальные данные "сглаживаются" с помощью функции φ(х). Если же выбрать m = n, то на основании единственности интерполяционного полинома получим функцию φ(х), совпадающую с каноническим интерполяционным полиномом степени n, аппроксимирующая кривая пройдет через все экспериментальные точки и величина Q будет равна нулю. Последнее обстоятельство используется для отладки и тестирования программ, реализующих алгоритмы МНК.

Запишем расширенную матрицу системы нормальных уравнений для базиса (5.4):

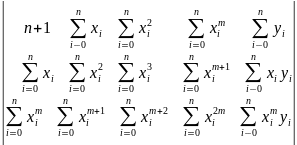
Нетрудно видеть, что для формирования расширенной матрицы (5.5)достаточно вычислить только элементы первой строки и двух последних столбцов, остальные элементы не являются "оригинальными" и заполняются с помощью циклического присвоения.

Пример 5.1. Рассмотрим линейную аппроксимацию экспериментальных данных, т.е. аппроксимацию в виде прямой y = ax + b. В этом случае m = 1

Запишем расширенную матрицу Грама для этого случая:

Тогда, используя метод Крамера, получим следующие расчетные формулы для коэффициентов аппроксимирующей прямой:

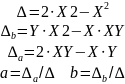
Пример 5.2. Аппроксимация функций в MATLAB.

x = [1 2 3 4 5];

y = [4 2 0 1 -2];

% Построим интерполяционный многочлен (аппроксимация первой степени)

p = polyfit(x, y, 1)

p =

-1.3000 4.9000

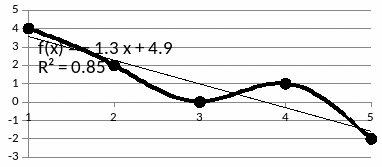
При аппроксимации полиномом второй степени получим

p =

0.0714 -1.7286 5.4000

Пример 5.2. Аппроксимация функций в Excel.

Исходные данные в таблице:

x	y
1	4
2	2
3	0
4	1
5	-2

Вычисленное уравнение линейной регрессии размещается на графике:

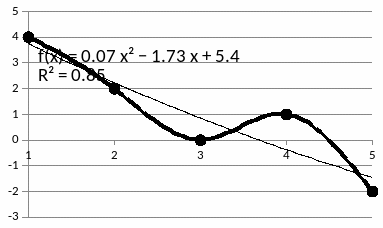
5.2. Базис в виде классических ортогональных полиномов

Выбор базисных функций φ_k(х) в виде степеней х (4.8) не является оптимальным с точки зрения решения системы нормальных уравнений с наименьшими погрешностями. Приемлемые результаты в этом случае можно получить, если набор экспериментальных данных с удовлетворительной погрешностью удается аппроксимировать полиномом невысокой степени(m< 4-5).

Лучшие результаты может дать использование классических ортогональных полиномов Чебышева, Лежандра, Лагерра, Якоби и других в качестве базисных функций. Свойство ортогональности классических полиномов заключается в том, что для каждого типа полиномов существует отрезок [x₀ – x_n] на котором обращаются в нуль скалярные произведения полиномов разного порядка с весовой функцией р(х):

В случае большого количества узлов х_j- на отрезке [x₀ – x_n] скалярные произведения будут близки к дискретным скалярным произведениям, так как интегрирование можно приближенно заменить суммированием.

Значит, недиагональные элементы матрицы Грама будут иметь небольшую абсолютную величину, что позволит уменьшить погрешность решения системы линейных уравнений.

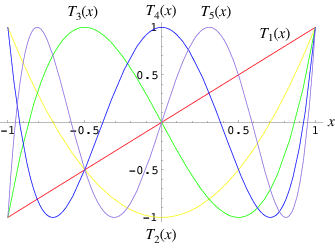
Разыскать определение полиномов Чебышева, построить графики 3-5 первых полиномов Чебышева.

Многочле́ны Чебышева— две последовательности ортогональных многочленов T_n(x), n={0, 1, …} названные в честь Пафнутия Львовича Чебышева.

Многочлены Чебышева первого родаT_n(x)могут быть определены с помощью рекуррентного соотношения:

Несколько первых многочленов Чебышева первого рода