6.2. Ряды Фурье.

Спектральный анализ периодических функций заключается в нахождении коэффициентов a_k, b_k ряда Фурье

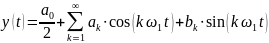
где ω₁ – круговая частота первой гармоники, k – номер гармоники.

Несложными преобразованиями это выражение приводится к другой эквивалентной форме:

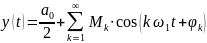
где амплитуда 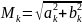и фаза сигнала

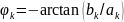
Коэффициенты ряда Фурье определяются выражениями

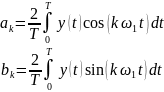
Численный спектральный анализ заключается в отыскании коэффициентов a_k, b_k для периодической функции y(t), заданной на отрезке [0, T] дискретными отсчетами. Он сводится к приближенному расчету заданных выше определенных интегралов. В итоге для случая равноотстоящих узлов заданной функции получим следующие вычислительные формулы:

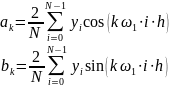
где N – количество отсчетов заданной функции; h = T/N – шаг, с которым расположены отдельные отсчеты.

Найденные таким образом коэффициенты Фурье приближают функцию y(t) рядом с наименьшей квадратичной погрешностью. Следовательно, численный спектральный анализ является разновидностью метода наименьших квадратов со специфическим базисом из тригонометрических функций.

Инструментарий – разработанная мною программа fourier.exe.

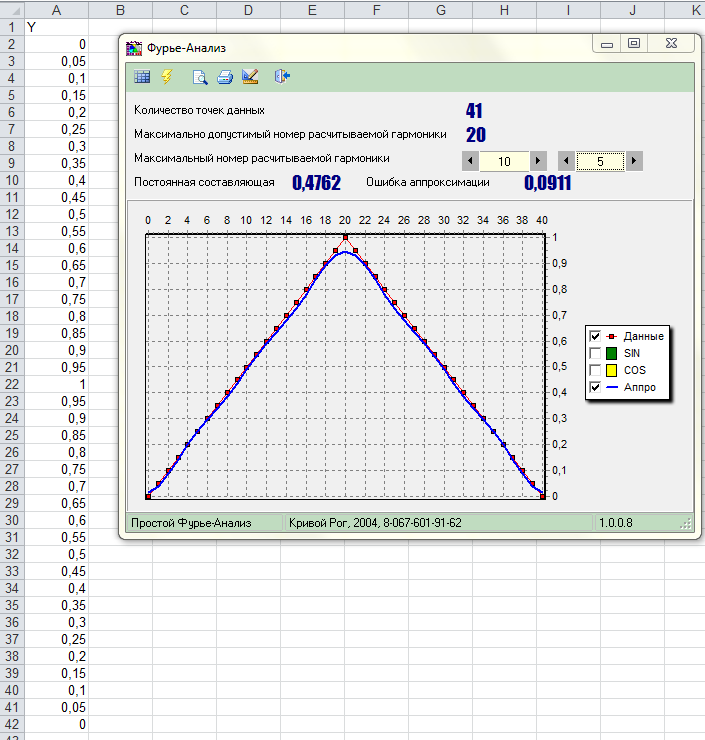
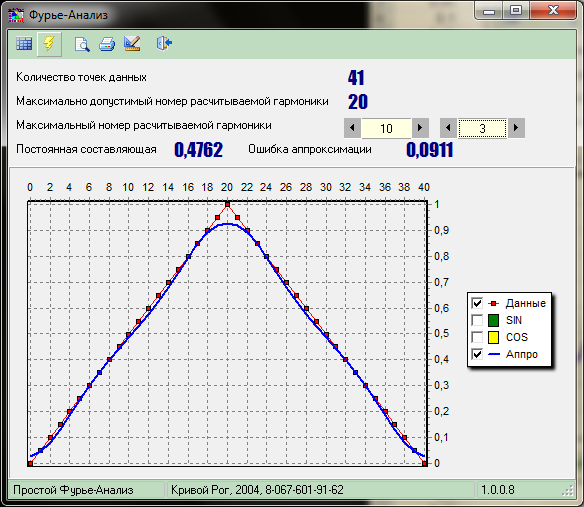
Рисунок 6.1 - Пример подготовки данных на рабочем листе MS EXCEL и главное окно программы для расчета высших гармоник периодической функции.

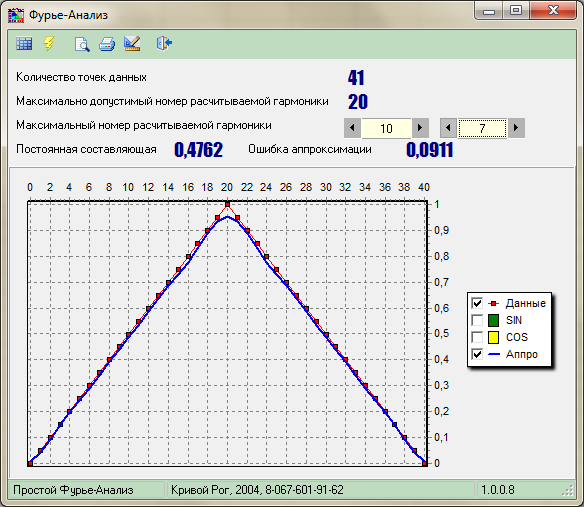
3 гармоники	7 гармоник
Рисунок 6.2 – Гармонический синтез функции по результатам аппроксимации рядом Фурье.

При моделировании периодических функций с разрывами возникают определенные особенности. Любой скачок функции содержит все частоты диапазона до бесконечности, в связи с чем ряд Фурье также бесконечен и очень медленно затухает. Аппроксимирующий полином не может точно «сшить» исходную функцию в точке разрыва,

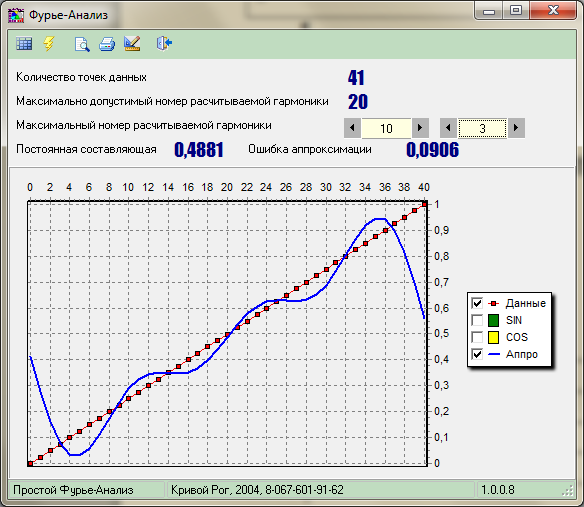
	3 гармоники
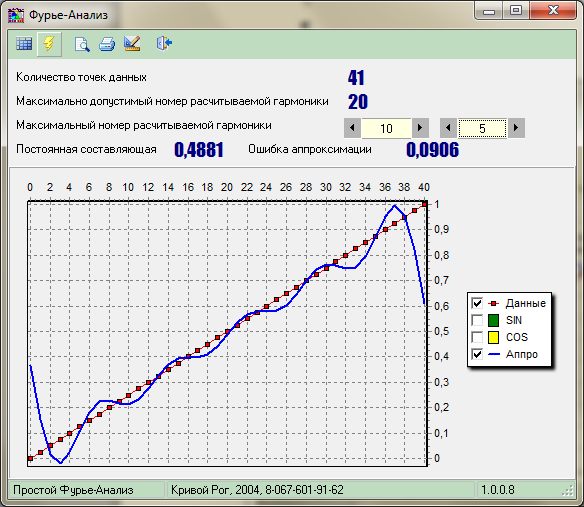
	5 гармоник
Рис.6.3. Демонстрация эффекта Гиббса при гармонической аппроксимации разрывных функций.

Принцип последовательного приближения к исходной форме наглядно виден на рисунке 6.3. На нем же можно видеть появления пульсаций на реконструкции скачков функций, которые носят название эффекта Гиббса. При изменении количества суммируемых членов ряда эффект Гиббса не исчезает. Не изменяется также относительная амплитуда пульсаций (по отношению к амплитуде скачка) и относительное затухание (по коэффициенту последовательного уменьшения амплитуды пульсаций по отношению к максимальному выбросу), изменяется только частота пульсаций, которая определяется частотой последних суммируемых гармоник. Эффект Гиббса имеет место всегда при резких нарушениях монотонности функций. На скачках эффект максимален, во всех других случаях амплитуда пульсаций зависит от характера нарушения монотонности функции.

6.3. Функции Уолша.

Преобразования, обсуждавшиеся ранее, были основаны на функциях косинус и синус. Намного проще и быстрее считаются преобразования, основанные на импульсно-подобных сигналах, которые принимают значения только ±1. Кроме того, они больше подходят для описания сигналов с нарушением непрерывности, которые встречаются, например, в изображениях. И. наоборот, они менее пригодны для описания непрерывных сигналов и могут не быть инвариантными по фазе, а если это так. полученный спектр может искажаться. Поэтому такие сигналы обычно используются при обработке изображений (астрономия и спектроскопия), кодировании сигналов и фильтрации.

Точно так же. как ДПФ основывается на наборе гармонических косинусоидальных и синусоидальных сигналов, дискретное преобразование Уолша (ДПУ) основано на наборе гармонических прямоугольных импульсов. которые называются функциями Уолша. Однако для прямоугольных импульсов частота не определена, поэтому используется аналоговый термин «последовательность». Последовательность - это половина среднего числа переходов через нуль за единицу времени. На рис. 6.4 показаны функции Уолша до порядка N= 8. расположенные по возрастанию.

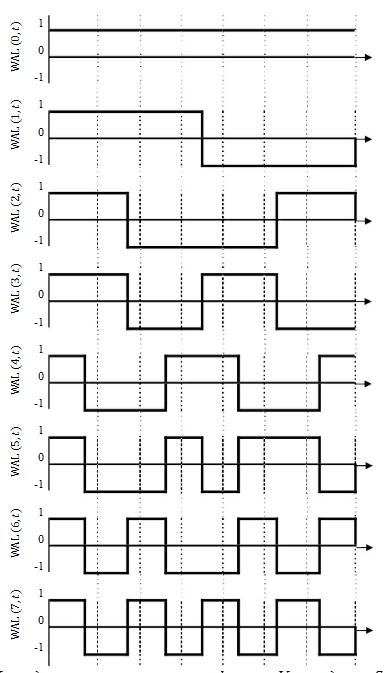
Рисунок 6.4 - Упорядоченные по возрастанию функции Уолша до n = 7

В таком виде их называют упорядоченными по Уолшу. Функция Уолша со временем t и порядком n обозначается WAL(n, t). Изучая рис. 6.4. видим. что существует равное количество четных и нечетных функций Уолша. точно так же. как и косинусоидальных и синусоидальных компонентов ряда Фурье. Четные функции WAL(2k, t) записываются как CAL(2k, t), а нечетные функции WAL(2k+1, t) записываются как SAL(2k+1, t), где к = 1, 2,....N/2-1.

Любой сигнал f(t) можно разложить по набору функций Уолша (аналог разложения в ряд Фурье) как

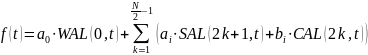
где a_i и b_i — коэффициенты ряда.