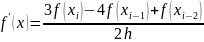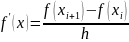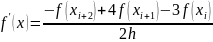9.1. Метод прямоугольников.

Рассмотрим сначала простейшие методы из класса методов Ньютона-Котеса, когда подынтегральную функцию f(x) на интервале интегрирования заменяем полиномом нулевой степени, т.е. константой. Подобная замена является неоднозначной, так как константу можно выбрать равной значению подынтегральной функции в любой точке в интервале интегрирования. Приближенное значение интеграла определится как площадь прямоугольника, одна из сторон которого есть длина отрезка интегрирования, а другая - аппроксимирующая константа. Отсюда происходит и название методов.

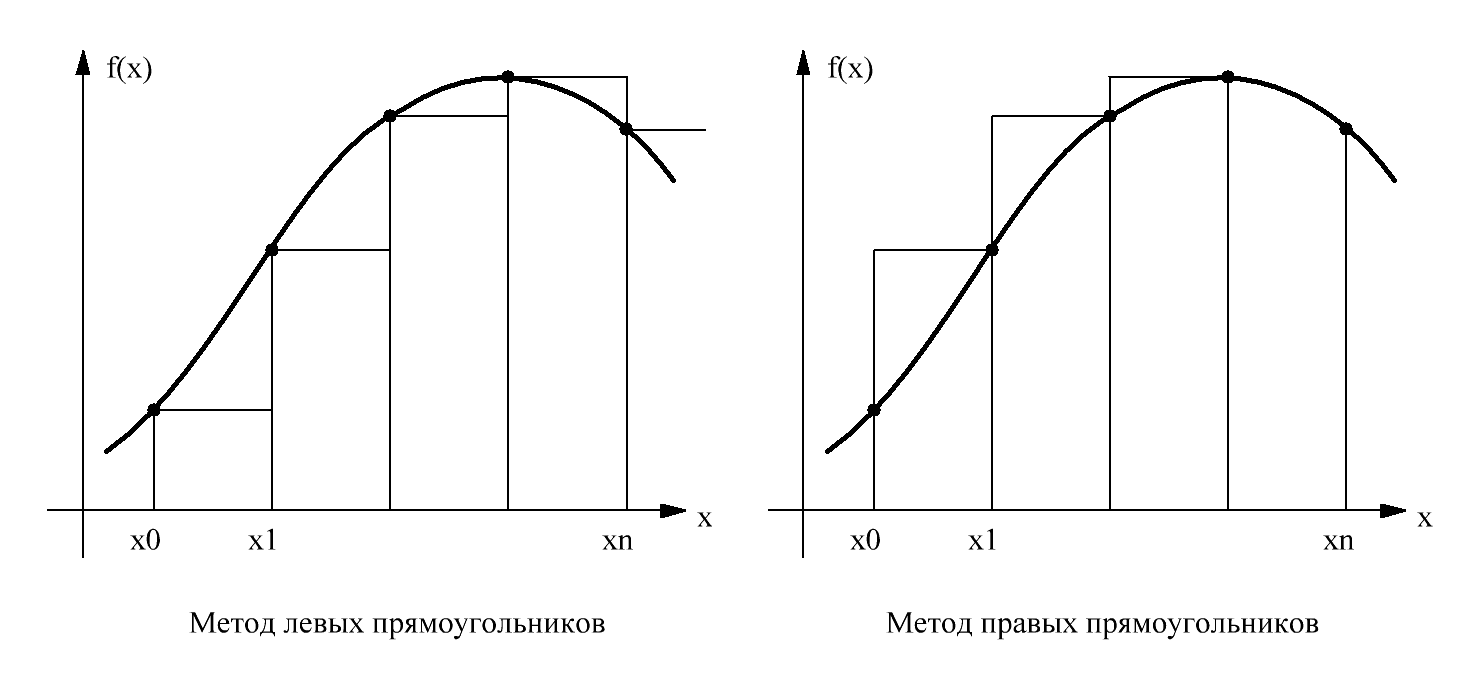
Рисунок 9.1 – Пояснения к расчету определенного интеграла методом прямоугольников.

Искомый интеграл будет равен соответственно для метода левых и правых прямоугольников

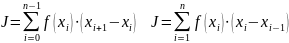
Методы левых и правых прямоугольников (рис. 9.1) имеют сравнительно высокую погрешность. Иногда применяют метод средних прямоугольников. Общая ошибка метода прямоугольников зависит от скорости изменения функции. Для быстро меняющихся функций ошибка будет больше, чем для медленно изменяющихся функций. Основной способ повышения точности вычислений – это уменьшение расстояния между отсчетами, уменьшение шага интегрирования.

9.2. Метод трапеций.

Очевидный способ повысить точность метода прямоугольников – заменить подынтегральную функцию на интервале [x_i-1, x_i] не константой, а участком прямой линии. При этом подынтегральная функция на каждом интервале расчетов заменяется трапецией, рис.9.2.

Рисунок 9.2 – Пояснения к расчету определенного интеграла методом трапеций.

Так как площадь элементарной трапеции равна полусумме оснований, умноженной на высоту, то искомый интеграл будет равен

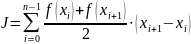
Пример 9.1. Демонстрация простейших методов интегрирования в программе MS Excel.

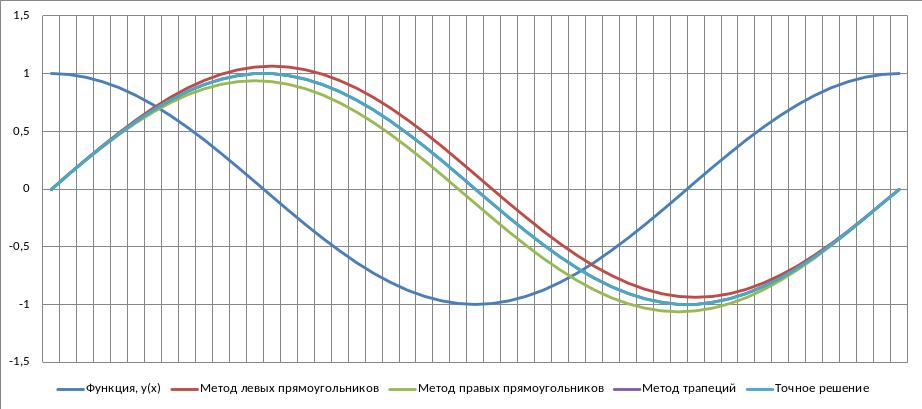
Рисунок 9.3 - Сравнительные графики интегралов косинуса, рассчитанных разными методами.

9.3. Метод Симпсона.

Подынтегральную функцию f(x) заменим интерполяционным полиномом второй степени Р₂(х) - параболой, проходящей -через узлы х₀, х₂ (рис. 9.3).

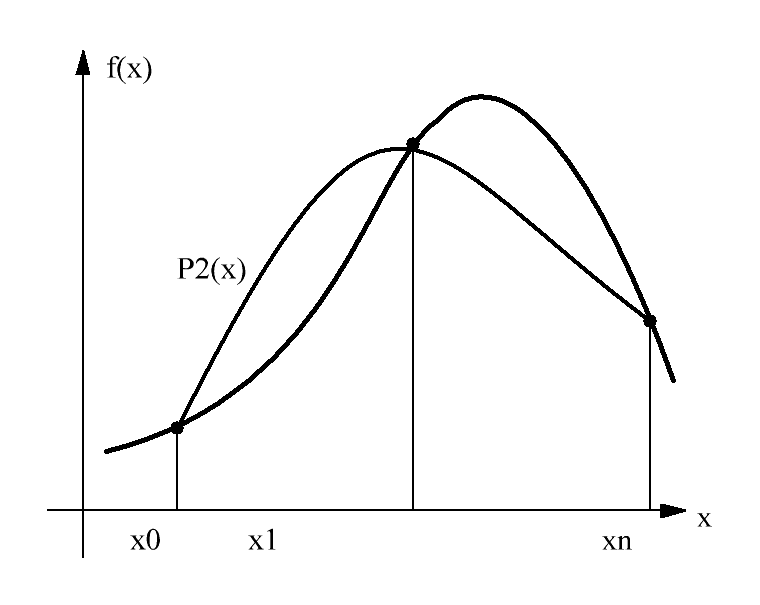
Рисунок 9.4 – Пояснения к расчету определенного интеграла методом Симпсона.

Известно, что по трем точкам можно провести единственную параболу. Коэффициенты уравнения параболы можно вычислить с помощью интерполяционного многочлена Ньютона, или из СЛАУ, составленной для трех имеющихся точек.

В конечном итоге получаем следующую квадратурную формулу:

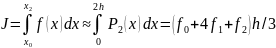
Это соотношение и называют формулой Симпсона или формулой парабол.

Формула Симпсона имеет четвертый порядок точности, т.е. ошибка формулы Симпсона зависит от величины четвертой производной исходной функции. Формула Симпсона позволяет получить высокую точность, если четвертая производная подынтегральной функции не слишком велика. В противном случае методы второго порядка могут дать большую точность, чем метод Симпсона.

Например [51], для функции f(x) = -25х⁴ + 45х² - 7 формула трапеций при n = 2 для интеграла в пределах [-1, 1] дает точный результат, равный 4, тогда как по формуле Симпсона получим результат, не совпадающий даже по знаку - (-8/3).

9.4. Численное дифференцирование.

Данный раздел посвящен вопросам вычисление производных заданных порядков. Если аналитическое изображение исходной функции неизвестно или довольно сложное, производные любого порядка могут быть вычислены на основе приведенных в разделе формул дифференцирования. Большинство формул численного дифференцирования могут быть получены на основе интерполяционных полиномов. Для этого достаточно заменить начальную функцию ее интерполяционным полиномом, а потом вычислить производные от него. Если полином с достаточной точностью приближает исходную функцию, то можно утверждать, что производной любого порядка от полинома мало будут отличаться от производных функции.

В качестве примера применения численного дифференцирования приведем известный и широко применяющийся на практике пропорционально-интегрально-дифференциальный регулятор – ПИД-регулятор. Алгоритм его функционирования задается выражением

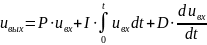
где P. I, D – числовые коэффициенты, устанавливаемые в процессе наладки для получения заданных показателей переходных процессов.

Особенностью технических систем является то, что зачастую мы не располагаем ни аналитическим описанием сигналов, ни даже таблицей значений входного сигнала.

Вспомним определение производной функции.

Из определения производной непосредственно следует простейшая формула для вычисления первой производной:

Эта формула может быть получена, если дифференцируемую функцию заменить отрезком прямой. Для вычислений используется текущее и предыдущее известное значение функции. Эта формула описывает так называемое дифференцирование «назад».

Очевидно, что если известна таблица значений функции, то можно определить производную функции, используя текущее и последующее значение – так называемое дифференцирование «вперед».

Приведем перечень практически применяющихся формул для численного дифференцирования таблично заданных функций.

Тип формулы	Формула
Несимметричные обратные, формулы дифференцирования «назад»
Несимметричные прямые, формулы дифференцирования «вперед»
Симметричные

Симметричные формулы в общем случае имеют более высокую точность, однако они неприменимы для реализации алгоритмов, работающих в реальном времени.

Пример 9.2. Демонстрация простейших методов дифференцирования в программе MS Excel. В примере с помощью трех формул первого порядка рассчитывается производная функции y=sin(x).

Сравнительные графики производных, рассчитанных разными методами, приведены на рис. 9.5.

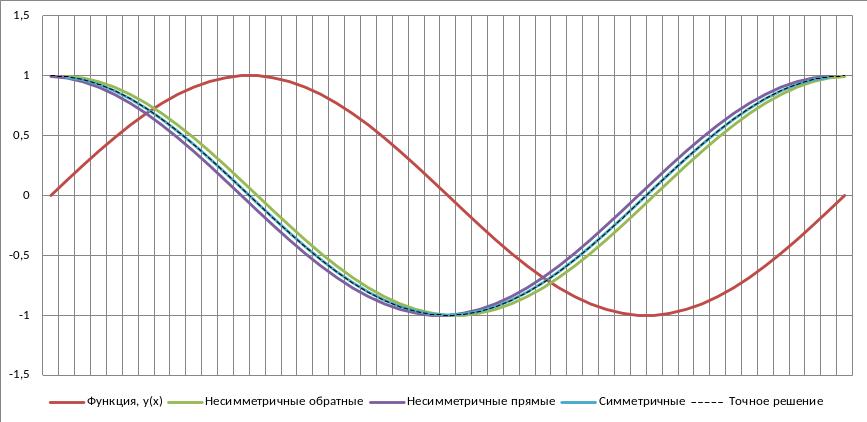
Рисунок 9.5 - Сравнительные графики производных синуса, рассчитанных разными методами.