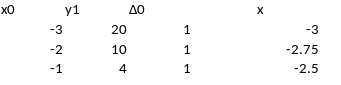Лекция 13. Решение оптимизационных задач.

13.1. Методы безусловной одномерной оптимизации

Ниже рассматривается решение наиболее простого типа задач оптимизации – поиска экстремума функций одной переменной без ограничений. Данная задача формулируется как нахождение такого значения вход-ной переменной объекта, которое соответствует наилучшему(минимальному или максимальному) значению целевой функции.

Хотя на практике задачи, в которых критерий задан функцией одной переменной, встречаются достаточно редко, анализ таких задач занимает достаточно важное место в оптимизационных исследованиях. Это объясняется тем, что многие многомерные методы используют на каждой итерации одномерные процедуры. Одномерные методы достаточно понятны, легко могут быть проиллюстрированы графически, что позволяет глубже понять сущность задач оптимизации и способствует приобретению навыков их решения.

Будут рассмотрены постановка задачи одномерной оптимизации, аналитический анализ функций и наиболее известные численные методы поиска экстремума: обратного переменного шага, квадратичной аппроксимации, половинного деления, золотого сечения.

13.1.1. Постановка задачи.

Одномерная оптимизация заключается в нахождении точки x*, в которой целевая функция f(x) принимает максимальное или минимальное значение. Часто в постановках задачи может быть задан отрезок[a, b], в котором находится оптимальное значение.

Функция f(x) имеет локальный минимум в точке x*, если при ε > 0 существует окрестность[x*- ε, x*+ ε] такая, что для всех значений x в этой окрестности f(x) больше f(x*)

Функция f(x) имеет глобальный минимум в точке x*, если для всех x справедливо неравенство f(x) > f(x*).

Целевая функция может иметь в заданной области несколько экстремумов. Поэтому различают задачи поиска локального и глобального максимумов. Ниже мы будем условно полагать, что в области поиска содержится единственный экстремум.

13.1.2 Метод обратного переменного шага.

Данный метод называют иногда методом сканирования.

Предположим, что произвольная точка x0 этого промежутка является исходной для поиска точки х* локального минимума и число ε– заданная точность нахождения х*.

Обозначим через Δ₀ произвольное приращение аргумента х и, сделав один шаг от точки x₀ , получим новое значение аргумента х₁= x₀+ Δ₀.

Сравним значения функции у₀= f(x₀) и у₁= f(x₁) = f(x₀+Δ₀). Возможны три различных продолжения в приближении к точке х *.

I. у₁ < у₀ - произошло уменьшение значения функции. Тогда примем в качестве нового стартового значения х₀⁽¹⁾ = х₁ , и сделаем шаг Δ₀ от этой точки х₀ ⁽¹⁾ к точке х₁ ⁽¹⁾ , т.е. х₁ ⁽¹⁾ = х₀ ⁽¹⁾ + Δ₀. Если окажется у₁ (1) < у₀ ⁽¹⁾ , то снова сделаем шаг Δ₀ от новой стартовой точки х₀ ⁽²⁾ = х₁ ⁽¹⁾ и т.д. На некотором k-м шаге произойдет увеличение значения функции, т.е. у1^(k)>у₀^(k), и если при этом|Δ₀| < ε, то принимаем х * ≈ х₀ ^(k). В противном случае полагаем, что точка x₀ ^(k) является исходной для продолжения вычислений по следующей схеме.

II. у₁> у₀ - значение функции возросло. В этом случае полагаем, что начальной точкой вычислений является точка х₀= х₁, а меньшим шагом в продолжении счета– величина Δ₁= - β Δ₀, где β – некоторое положительное число, β< 1. Далее производим вычисления по схеме I или II, вплоть до достижения заданной точности.

Поиск минимума функции одной переменной указанным методом представляет собой колебательный процесс, совершающийся около точки х* локального минимума функции f(x) с непрерывно меняющейся амплитудой.

Пример 13.1. Поиск экстремума методом сканирования. В качестве исследуемой функции возьмем параболу y = 3x²+2, имеющую минимальное значение y_min=y(0)=2.

Ниже приведены исходные данные и графическое отображение как исследуемой функции так и процесса поиска минимума.