13.2.2. Метод наискорейшего спуска (метод градиентов)

Известно, что градиент функции f(z_lf z₂, z_n) в каждой точке направлен в сторону наискорейшего локального возрастания этой функции. Следовательно, для поиска минимума необходимо спускаться в противоположном направлении. Если минимизируемая функция дифференцируема и ограничена снизу, а ее градиент удовлетворяет условию Липшица, то итерационный процесс

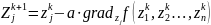
будет сходиться к минимуму функции f из произвольной начальной точки с координатами z⁰₁, z⁰₂,..., z⁰_n.

Параметр a в формуле (8.7) определяет длину шага в направлении спуска. Длину шага можно выбирать из условия минимизации функции вдоль направления, противоположного градиенту. Такой вариант градиентного метода называют методом наискорейшего спуска. В другом варианте градиентного спуска длина шага а выбирается методом дробления. С помощью градиентного спуска минимум гладких функций находится значительно быстрее, чем при использовании координатного спуска. Однако наряду с вычислением функции f на каждой итерации градиентного метода приходится вычислять составляющие градиента этой функции. Кроме того, сходимость итерационного процесса может быть медленной для функций, имеющих овражный рельеф. В этом случае изменением масштабов переменных рекомендуется перейти к котловинному рельефу или применить так называемый овражный метод.

В окрестности точки минимума составляющие градиента функции имеют малые значения, что приводит к возрастанию чувствительности итерационного процесса к погрешностям вычислений и осложняет поиск на заключительном этапе.

13.2.3. Метод Нелдера-Мида.

Метод Нелдера — Мида, также известный как метод деформируемого многогранника и симплекс-метод, — метод безусловной оптимизации функции от нескольких переменных, не использующий производной (точнее — градиентов) функции, а поэтому легко применим к негладким и/или зашумлённым функциям.

Суть метода заключается в последовательном перемещении и деформировании симплекса вокруг точки экстремума. В двухмерном пространстве регулярным симплексом является правильный треугольник, а в трехмерном - правильный тетраэдр.

Идея метода состоит в сравнении значений функции в (n+1) вершинах симплекса и перемещении симплекса в направлении оптимальной точки с помощью итерационной процедуры. В симплексном методе, предложенном первоначально, регулярный симплекс использовался на каждом этапе. Нелдер и Мид предложили несколько модификаций этого метода, допускающих, чтобы симплексы были неправильными. В результате получился очень надежный метод прямого поиска, являющийся одним из самых эффективных при N<7.

Метод находит локальный экстремум и может «застрять» в одном из них. Если всё же требуется найти глобальный экстремум, можно пробовать выбирать другой начальный симплекс.

Опишем идею этого метода применительно к функции двух переменных для поиска максимума функции z = f(x, y).

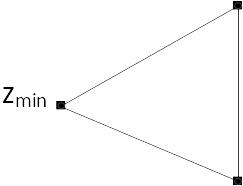
В начале расчета задается начальный симплекс – для 2-мерного случая – правильный треугольник, и вычисляются значения функции в вершинах треугольника, рис.13.3, а.

а)	б)	в)	г)
Рисунок 13.3 – Пояснения к алгоритму поиска экстремума Нелдера-Мида.

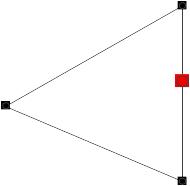
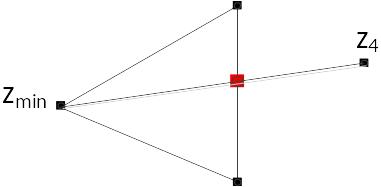
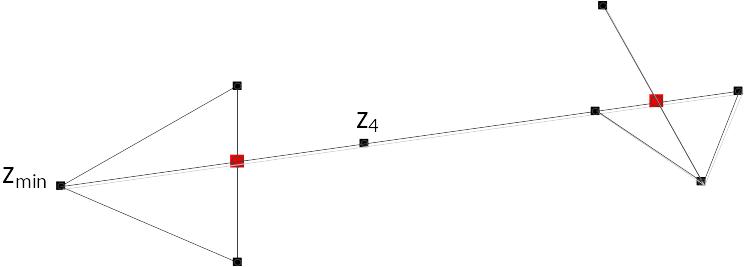
Отделяется вершина с наименьшим значением функции z_min. Для оставшихся двух вершин треугольника находим центр тяжести (рис.13.3, б) и проводим прямую через неудачную вершину и центр тяжести. От найденного центра тяжести в найденном направлении делаем шаг поиска, находим координаты новой точки z₄ (рис.13.3, в). Если в точке z₄ найдено новое максимальное значение, то делаем очередной шаг в этом же направлении. Если очередной шаг приводит к уменьшению функции, то в той точке производится отражение симплекса, выбирается новое направление движения (рис.13.3, г).

Метод Нелдера-Мида чем-то сходен с покоординатным спуском, однако здесь движение производится в направлении потенциально максимального градиента.

Главными особенностями алгоритма можно назвать следующее:

• Метод Нелдера-Мида не накладывает ограничений на гладкость функции

• Данный метод является эффективным при низкой скорости вычисления минимизируемой функции. Как правило, на каждой итерации происходит вычисление значения функции не более чем в 3 точках.

• Отсутствие теории сходимости. Алгоритм может расходиться даже на гладких функциях.