Хід роботи

Як приклад розглянемо таку систему лінійних рівнянь

4x₁ – x₂ + 2x₃ = 1,75;

x₁ – 5x₂ + 3x₃ = 2,5;

2x₁ + x₂ – 8x₃ = –0,25.

В матричній формі ці рівняння записуються таким чином

=

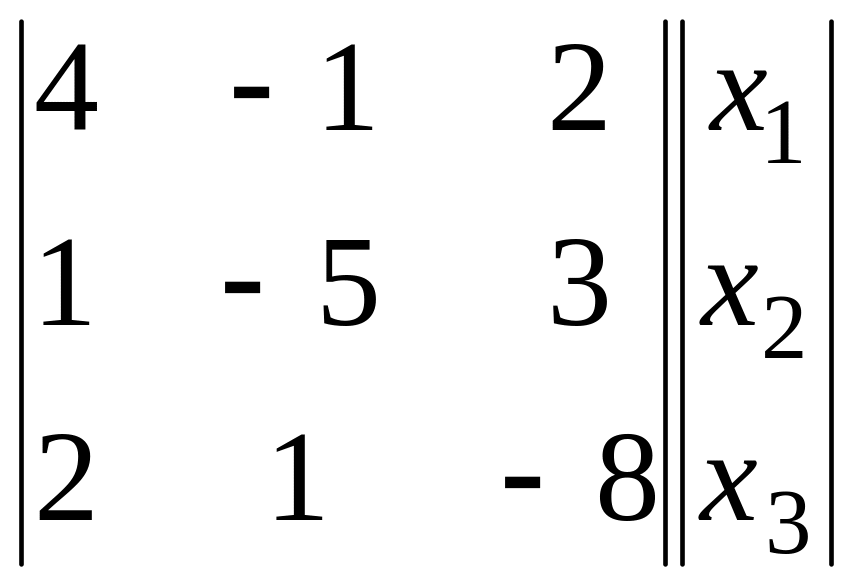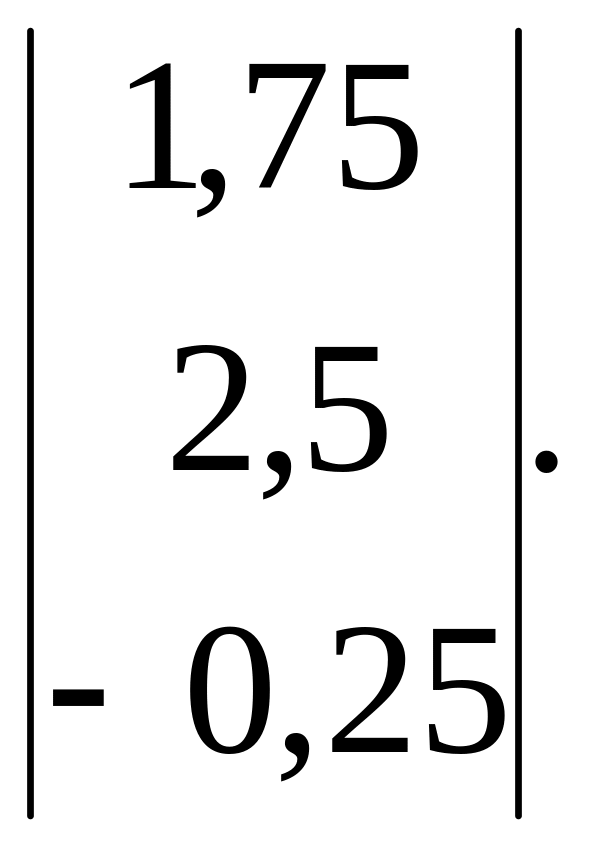
Таку систему можна розв’язати за допомогою електронної таблиці. Для цього.

1. Створити новий лист та дати йому ім'я ЛР№3.

2. В комірці А1 ввести текст Розв’язання систем рівнянь; обернення матриці.

3. В комірці В3 ввести текст Ах=b.

Тепер введіть матрицю коефіцієнтів А та вектор правої частини b.

4. В комірці А5 ввести текст Вхідна матриця(А).

5. В комірках А6:С8 введіть елементи матриці А:

Комірка	Значення	Комірка	Значення	Комірка	Значення
А6	4	В6	–1	С6	2
А7	1	В7	–5	С7	3
А8	2	В8	1	С8	–8

6. В комірці Е5 ввести текст Права частина (b).

7. В комірках Е6:Е8 ввести компоненти вектора правої частини:

Комірка	Значення	Комірка	Значення	Комірка	Значення
Е6	1,75	Е7	2,5	Е8	-0,25

Далі необхідно обернути матрицю А та помножити вектор b на матрицю, яка є оберненою до матриці А. Функція МОБР(), що застосовується для цього, повертає масив значень, що вставляється зразу в цілий діапазон комірок:

8. В комірці А10 ввести текст Обернена матриця (1/А).

9. Виділити комірки А11:С13, ввести таку формулу =МОБР(А6:С8) і натиснути клавіші <Ctrl+Shift+Enter> для вставки цієї формули у всі вибрані комірки.

10. В комірці Е10 ввести текст Розв'язок х=(1/А)b.

11. Виділити комірки Е11:Е13 та ввести таку формулу =МУМНОЖ(А11:С13;Е6:Е8), а потім натисніть клавіші <Ctrl+Shift+Enter> для вставки формули у всі вибрані комірки.

12. Відключіть відображені лінії сітки та обведіть комірки контуром.

Робочий лист до цього моменту повинен виглядіти так, як на рис. 5. В комірках Е11–Е13 повинні стояти значення компонентів вектора розв’язку х₁, x₂, x₃.

Контрольні питання

1. Як класифікуються наближені методи розв’язання СЛАР?

2. У яких випадках рекомендується використовувати прямі методи розв’язання СЛАР?

3. У яких випадках рекомендується використовувати ітераційні методи розв’язання СЛАР?

4. Що розуміється під коефіцієнтом щільності матриці?

4 Розв’язання систем лінійних алгебраїчних рівнянь ітераційним методом

Мета роботи – вивчення ітераційних методів і набуття навичок розв’язання систем лінійних алгебраїчних рівнянь із застосуванням Microsoft Excel'2000.

План роботи

1. Виписати з таблиці 4 систему лінійних алгебраїчних рівнянь відповідно до порядкового номера бригади студентів в журналі академгрупи.

2. Підготувати вихідні дані, перевірити на збіжність та розв'язати систему рівнянь методом Зейделя з точністю  = 0,00001.

Таблиця 4

Варіант
1	2	3	4	5
1	1,18 0,12 –0,07	–0,08 –0,43 0,34	–0,25 0,14 –0,72	1,12 –0,17 0,62
2	1,2 0,2 –0,3	–0,2 16 0,1	0,3 –0,1 –1,5	–0,6 0,3 0,4
3	0,63 0,05 0,15	0,05 0,34 0,10	0,15 0,10 0,71	0,34 0,32 0,42
4	1,21 –0,27 –0,34	–0,27 1,69 0,18	0,30 –0,14 –1,52	–0,61 0,33 0,44
5	0,31 –0,10 –1,51	1,27 –0,24 –0,37	–0,22 1,62 0,15	–0,67 0,37 0,45
6	8,24 1,15 2,11	2,02 10,60 –1,24	–1,46 5,55 –4,49	2,35 1,40 1,75
7	3,11 –1,65 0,60	–1,66 3,51 0,78	–0,60 –0,78 –1,87	–0,92 2,57 1,65
8	6,61 0,99 2,90	0,97 –4,52 –0,59	–0,94 –2,35 –5,33	4,96 1,81 –6,79

Продовження таблиці 4

1	2	3	4	5
9	5,43 –1,30 2,33	1,93 8,31 –0,49	3,24 5,44 4,28	48,50 50,23 30,78
10	7,6 2,2 –1,3	0,5 9,1 0,2	2,4 4,4 5,8	1,9 9,7 –1,4