Міністерство освіти і науки України

Вінницький національний технічний університет

Дослідження рекурсивних цифрових фільтрів

Лабораторна робота №2

Виконали студенти гр. ТКТ-12мс

__________________________

__________________________

Вінниця ВНТУ 2004

Мета роботи:

дослідження характеристик і параметрів рекурсивних цифрових фільтрів з різним типом апроксимації передаточної функції.

Досліджувальна та вимірювальна апаратура:

1. Комп’ютерна апаратура.

2. Робоча програма.

Короткі методичні вказівки до розрахунку:

Рекурсивний фільтр реалізує алгоритм обробки, описуваний різницевим рівнянням:

(2.1)

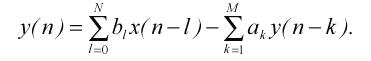
Виконаємо Z-перетворення лівих і правих частин (2.1), з огляду на властивості лінійності і затримки Z-перетворення:

(2.2)

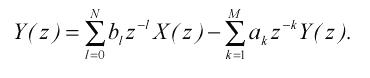
Переходячи до відношення Y(Z)/X(Z), отримаємо загальний вираз для передатної функції рекурсивного фільтра :

(2.3)

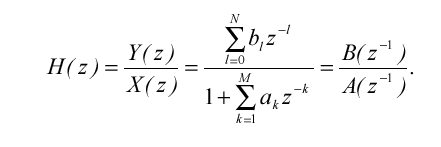
Воно представляє відношення двох поліномів по ступінях комплексної змінної Z^-1 . Його можна розглядати також як добуток двох передатних функцій : нерекурсивної частини фільтра

і рекурсивної частини фільтра

,

тобто

Вираз передатної функції (2.3) щодо перемінної Z , яка визначає затримку на один період дискретизації , зручний тім , що по ньому можна формально скласти відповідне передатної функції різницеве рівняння системи , яку визначає її алгоритм обробки .

На зіставленні різницевого рівняння (2.1) і передатної функції (2.3), можна безпосередньо записати вираз для передатної функції системи по її відомому різницевому рівнянню , не прибігаючи , як вище , до його Z-перетворення .

Структурне представлення дискретних систем , може бути виконано як по різницевому рівнянню , так і по передатній функції .

У виразі (2.3) передатної функції , як і різницевого рівняння (1), передбачається , що порядок N полінома не перевищує порядкові M полінома , що визначає порядок цифрового фільтра М , тобто виконується умова N<M. У випадку N >M передатна функція (2.3), отримана по різницевому рівнянню (2.1), діленням чисельника на знаменник приводиться до суми двох передатних функцій, перша з яких відповідає передатної функції нерекурсивного фільтра (N- M)-го порядку , а друга передатної функції рекурсивного фільтра , порядок чисельника якої завжди менше М.

(2.4)

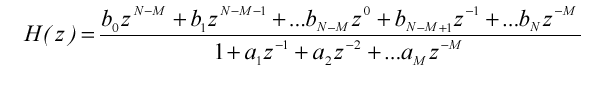
Якщо у виразі (2.4) N < M, те відповідне різницеве рівняння буде мати вигляд :

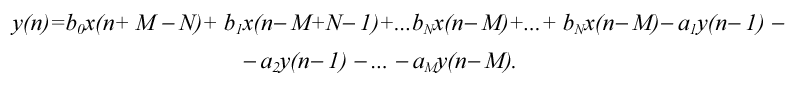
Отут відліки вхідного сигналові x(n), x(n-1), ... x(n-M+N+1) не використовуються при обчисленні y(n), що рівнозначно запізнюванню відгуку фільтра на (M- N) відліків .

Таким чином, передатні функції рекурсивного фільтра у формі (2.4) можуть бути узагальнено представлені відношенням двох поліномів B(z) і A(z) однакового порядку N=M:

(2.5)

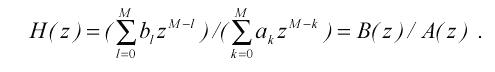
Передатні функції (2.3), (2.4) з N < M приводяться до (2.5) прирівнюванням до нуля коефіцієнтів b _l при N < l < M.

У приведених вище варіантах поліноміальної форми передатної функції коефіцієнти поліномів b0 і a0 ( l= k= 0) грають масштабуючу роль і можуть бути покладені рівними одиниці .

По передатній функції у формі (2.5) знаходяться її нулі і полюси , яки грають головну роль при синтезі й аналізі рекурсивних фільтрів .

Нулі передатної функції є коренями чисельника (2.5), тобто значеннями перемінної z, що звертають у нуль поліном B(z):

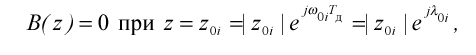
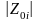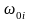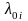де -модуль, -кутова частота і - цифрова частота нуля

Полюси відповідають кореням знаменника передатної функції, тобто

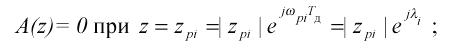
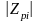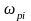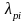де -модуль, -кутова частота і - цифрова частота нуля

Індекс i означає номер нуля і полюса : i = 1 , 2,…М , а М – число їх , рівне порядкові фільтра . Цифрові фільтри з дійсними коефіцієнтами a_k, b_l мають дійсні (у частці випадків нульові ) і / або комплексно -сполучені нулі і полюси . Нулі і полюси можуть бути простими і кратними . Якщо порядок чисельника передатної функції N менше порядкові знаменника М , ті такий фільтр має (М-N) нулів, рівних нулеві, тобто розміщених на початку координат комплексної Z-площини. Знаючи нулі і полюси передатної функції, її можна представити в так називаної нуль – формі , використовуючи розкладання поліномів чисельника і знаменника на елементарні співмножники :

(2.6)

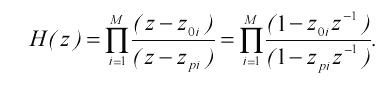
У вираженні (2.6) може бути присутнім множник, що нормує C=b₀/a₀, якщо коефіцієнти b₀ і a₀ передатної функції не дорівнюють одиниці .

Передатної функції (2.3) відповідає частотна характеристика РФ виду

( 2.7 )

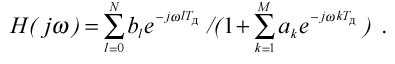
Приведення (2.7) до показникової форми приводить до аналітичних виражень для модуля |H(j )| і аргументу

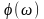
частотної характеристики , тобто до АЧХ і ФЧХ.

Передатної функції РФ у нуль - формі (2.6) відповідає вираз для ЧХ , що вказує спосіб її графо –аналітичного обчислення :

(2.8)

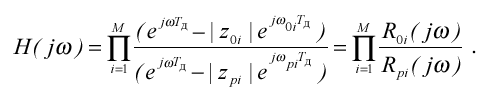
Чисельник і знаменник (2.8) уявляють векторні відстані R_0i ,R_pi від крапки на одиничній окружності з кутовою координатою Т відповідно до нулів Z_0i і полюсів Z_pi РФ . Перехід до модуля й аргументу (2.8) дає вираження для АЧХ і ФЧХ РФ у вигляді:

(2.9)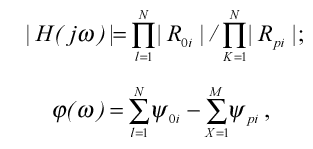

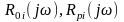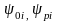де |R_0i|, |R_pi| довжини векторів , а – кути , утворені ними з віссю абсцис. Розташувавши нулі і полюсы на комплексній Z-площині (див. рис.2.1) і виміривши модулі і кути векторів , що з'єднують їх із крапкою на одиничної окружності що відповідає заданій частоті , наприклад з крапкою А на рис.2.1, за допомогою рівнянь (2.9) можна обчислити АЧХ і ФЧХ фільтра для будь-яких значень частоти сигналу в діапазоні (0 .. _д /2).

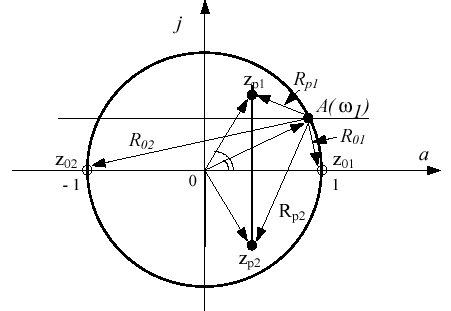
Рисунок 2.1 Картина нулів і полюсів цифрового фільтру.

Таким чином, положення нулів визначає смугу пропускання частотної характеристики фільтра , а положення нулів – її смугу затримування. По картині нулів і полюсів на комплексній площині судять також про сталість РФ . Полюси стійкого РФ , що не перевищують по модулю одиницю (|Z_pi|<1), знаходяться усередині кола одиничного радіуса . Для сталого аналогового фільтра полюси знаходяться в лівої частині комплексної площини, а при Z-перетворенні відображається усередину кола одиничного радіуса .

Рекурсивні фільтри здійснюють обробку сигналу у відповідності с різницевим рівнянням. Основними формами їхньої реалізації є пряма , канонічна та каскадна. Різницеві рівняння включають обчислювальні операції множення, підсумовування і затримки .

На структурних схемах і при апаратній реалізації ЦФ їм відповідають елементи цифрової затримки або пам'яті, помножувачі і суматори.

РФ порядку вище другого реалізуються , як правило, шляхом послідовного з'єднання базових ланок другого порядку , що відповідає каскадної формі їхньої реалізації. Базові ланки РФ виконуються в відповідності з прямою або канонічної формами реалізації РФ. Число послідовних ланок L при парному порядку фільтра M знаходиться як L=М /2, а при непарному – як L=(M+1 )/2, при цьому одна ланка фільтра є ланкою першого порядку ( з одним дійсним полюсом ).

Передатна функція каскадно реалізованого РФ (рис.2.2) визначається добутком передатних функцій його ланок :

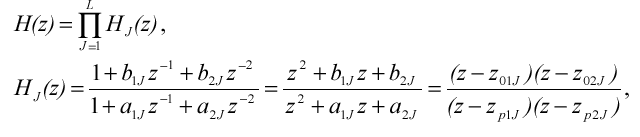
де H_J(z)-передатна функція J-ої біквадратної ланки при значенні

коефіцієнта b_0J = 1; С ₀ – множник , що нормує або масштабує .

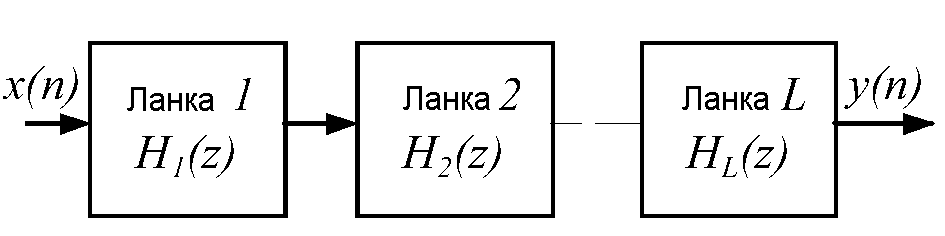
Рисунок.2.2 Каскадна структура ЦФ

Для ланки першого порядку коефіцієнти b_2J і a_2J дорівнюють нулеві .

Вхідним сигналом J-го ланки x (n) у такій структурі є вихідний сигнал y_J-1 (n) попередньої (J-.1)-го ланки : x (n) = y_J-1 (n).

Коефіцієнти ланок і їх полюси, нулі зв'язані співвідношеннями :

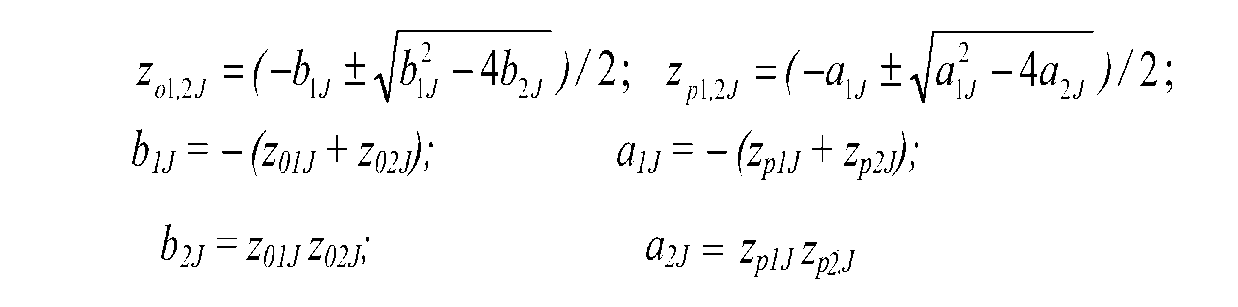
Структуру ланки 2-го порядку показано на рис.2.3.

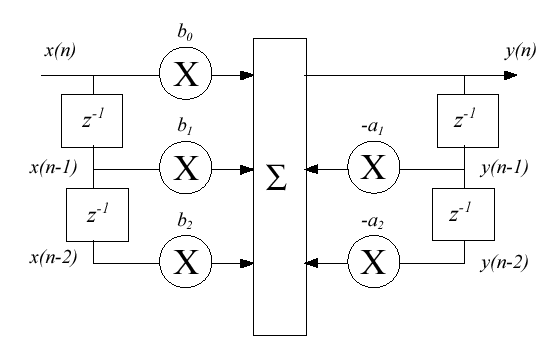
Рисунок 2.3 Cтруктура биквадратного звена

Синтез РФ по аналоговому прототипі можливий з використанням методу билинейного перетворення. У цьому методі синтезованому ЦФ ставиться у відповідність деякий аналоговий фільтр – прототип ( АФП ) з передатною функцією H(p) і частотною характеристикою H(j), однозначно зв'язани з передатною функцією H(z) і частотною характеристикою Н (j) ЦФ :

АФП : ЦФ : АФП : ЦФ :

Зв'язок визначається прямою p= f(z) і зворотньою z = f^--1 (p) перетворюючими функціями. За допомогою цих перетворень визначаються вимоги до АФП , по яких добре розробленими методами синтезується його передатна функція H(p), перетворена потім у шукану передатну функцію ЦФ H(z).

Перетворюючі функції повинні задовольняти наступної умовам :

Ліва напівплощина , у якій розміщаються полюсы p =+ j ,  < 0, стійкого АФП , повинна однократно відображатися усередину кола одиничного радіуса |z| < 1 , у якому на Z-площині розміщаються полюси стійкого ЦФ , тобто стійкому АФП повинний відповідати стійкий ЦФ ;

уся уявна вісь частот повинна однократно , тобто в один обхід , відображатися на окружність одиничного радіуса Z-площини, забезпечуючи близькість частотних характеристик обох фільтрів .

Цим умовам відповідає білінійне перетворення.

Синтез аналогових фільтрів з різними типами АЧХ (ФНЧ , ФВЧ , СФ, СЗФ ) виконується по нормалізованому аналоговому ФНЧ-прототипу. Представляється зручним використання нормалізованого аналогового ФНЧ і як прототип при синтезі ЦФ . При цьому кожному типові ЦФ ставиться у відповідність узагальнене білінійне перетворення p = f (z) і відповідне йому частотне перетворення =f(), що безпосередньо встановлюють зв'язок між передатною функцією і частотною характеристикою АФПНЧ і ЦФ заданого типу і виключають необхідність яких – додаткових проміжних перетворень .

Синтез АФПНЧ включає вибір апроксимуючої функції , визначення порядку фільтра m, значень нулів і полюсів передатної функції по заданих граничних частотах  і допускам на похібки апроксимації. Синтез виконуєтся по довідниках або за допомогою спеціальних комп′ютерних программ .

До поліноміального типу апроксимації відносяться апроксимації Баттерворта, Чебишева, до дробових – Кауэра ( еліптичні фільтри ). Передатні функції фільтрів з поліноміальною апроксимацією не мають кінцевих нулів, їхні частотні характеристики монотонні в смузі затримування .У фільтрів із дробовою апроксимацією передатні функції мають нулі на кінцевих частотах у смузі затримування, а частотні характеристики – пульсації ( тому числі рівнохвильові ) у цій смузі . Фільтри Чебишева й еліптичні мають рівнохвильові пульсації й у смузі пропущення.

Для частотних характеристик з рівнохвильовими пульсаціями на графіках зазначені відповідні ним частоти нулів і полюсів .

Фільтри з дробовою апроксимацією забезпечують кращі характеристики загасання при однаковому порядку фільтра або менше значення порядку при заданому загасанні частотної характеристики.

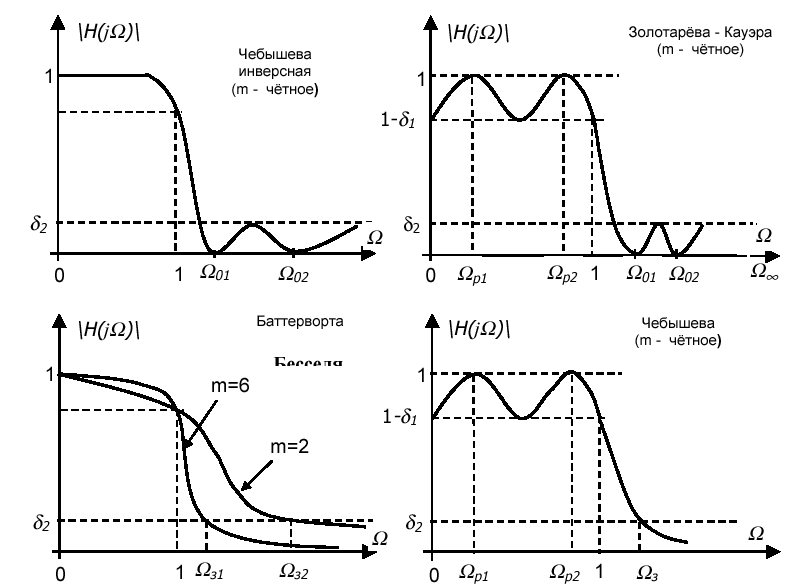
Рисунок 2.4 Графіки частотних характеристик нормалізованого

АФПНЧ , відповідні різним апроксимуючим функціям

Типові графіки частотних характеристик нормалізованого АФПНЧ з поліноміальною і дробовою апроксимаціями приведені на рис. 2.4.

Синтез РФ включає наступні етапи :

1. За допомогою частотних перетворень по заданим значенням граничних частот ЦФ находятся граничні частоти аналогового ФНЧ.

2. По значениям затухань в смугах пропускання і затримки синтезуєтся АФПНЧ : выбирается тип апроксимуючої функції , визначаються порядок фільтра m і значення його полюсів і нулів.

3. Розраховуються значення полюсів і нулів ЦФ заданого типу :

4.Обирається структура фільтра і розраховуються коефіцієнти її ланок.

5. Розраховується АЧХ і ФЧХ фільтра і зіставляється з заданою .

6. Знаходиться мінімально необхідна розрядність коефіцієнтів фільтра, при якій АЧХ ще задовольняє заданим вимогам (параметрам нерівномірності і загасання ).

7. Вирішуються задачі, зв'язані з кінцевою розрядністю чисел і моделюванням фільтра на ЕОМ.